Динамика машинного агрегата. Постановка задачи динамического синтеза и анализа машинного агрегата. Задачей динамического синтеза машинного агрегата является определение постоянной составляющей приведенного момента инерции, при которой колебания угловой скорости звена приведения не превышают допускаемой величины, заданной коэффициентом неравномерности вращения . Определение необходимой величины момента инерции маховика Iм. Задачей динамического анализа является определение угловой скорости и углового ускорения звена приведения с учетом приведенного момента инерции . Структурный анализ рычажного механизма двигателя внутреннего сгорания. Схема для исследования механизма. 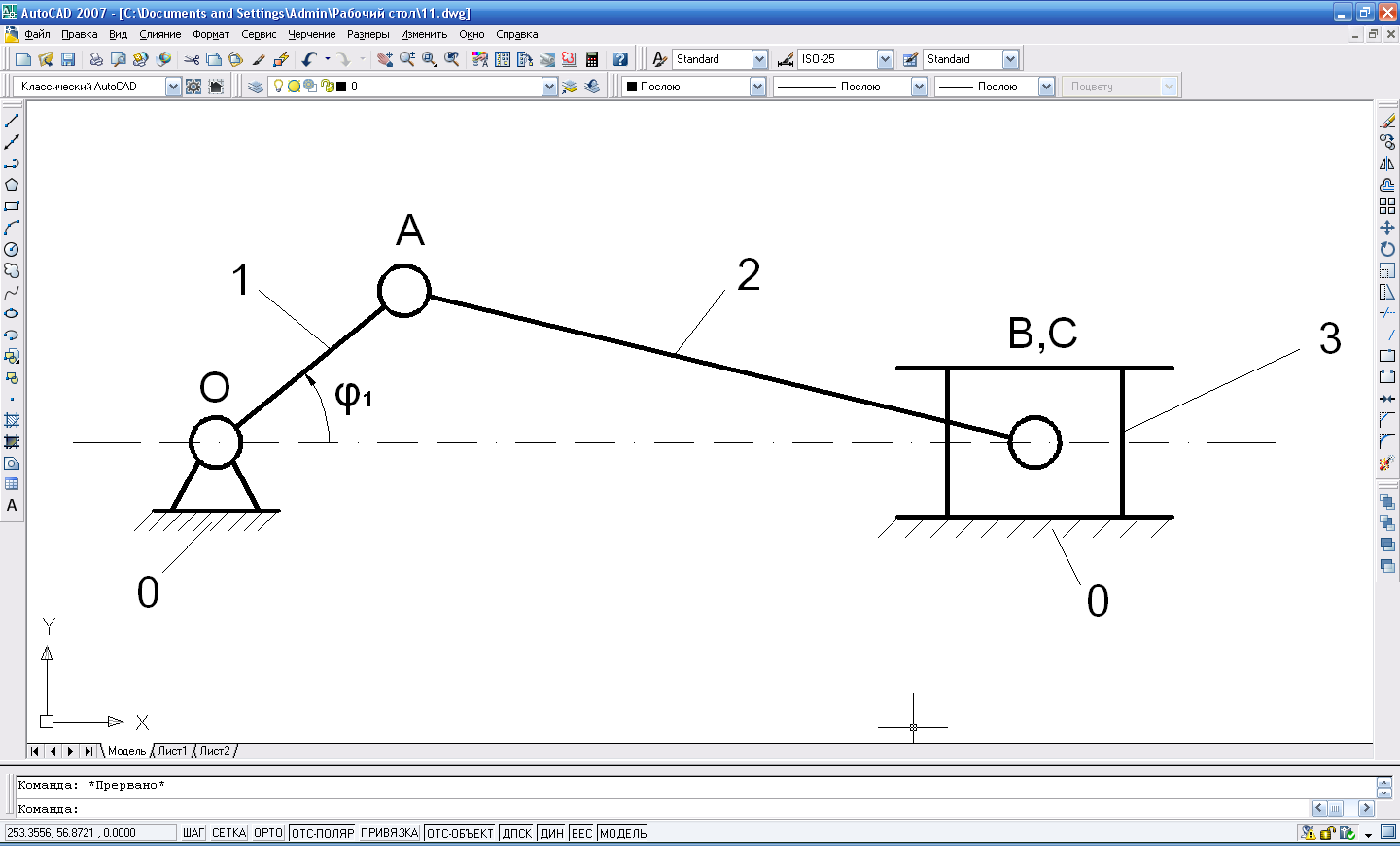Рисунок 3.1. Структурная схема механизма. На Рисунке 3.1. изображена схема исследуемого механизма, в которую входят следующие звенья: неподвижное звено (стойка); кривошип (коленчатый вал); шатун; ползун (поршень). Число всех звеньев механизма m=4. Число подвижных звеньев n=3. Определение класса кинематических пар: О(0-1)- вращательная, одноподвижная, 5 класса; А(1-2)- вращательная, одноподвижная, 5 класса; B(2-3)- вращательная, одноподвижная, 5 класса; С(3-0)- поступательная, одноподвижная, 5 класса.
						Курсовой проект по ТММ
Изм.	Кол.	Лист	№док	Подпись	Дата
Разраб.		Беганский А.В.				Пояснительная записка	Лит	Лист	Листов
Проверил		Кудин В.В.
							гр.101129
Н. контр.
Утв.

Число высших пар - .

Число низших пар - .

Для определения степени подвижности воспользуемся формулой Чебышева, так как механизм плоский.

где n-число подвижных звеньев; - число низших пар; - число высших пар.

.

Это означает, что кривошипно-ползунный механизм двигателя внутреннего сгорания обладает одной независимой координатой, в качестве которой принимаем угол поворота кривошипа .

Разбиваем механизм на группы Ассура и механизм I класса:

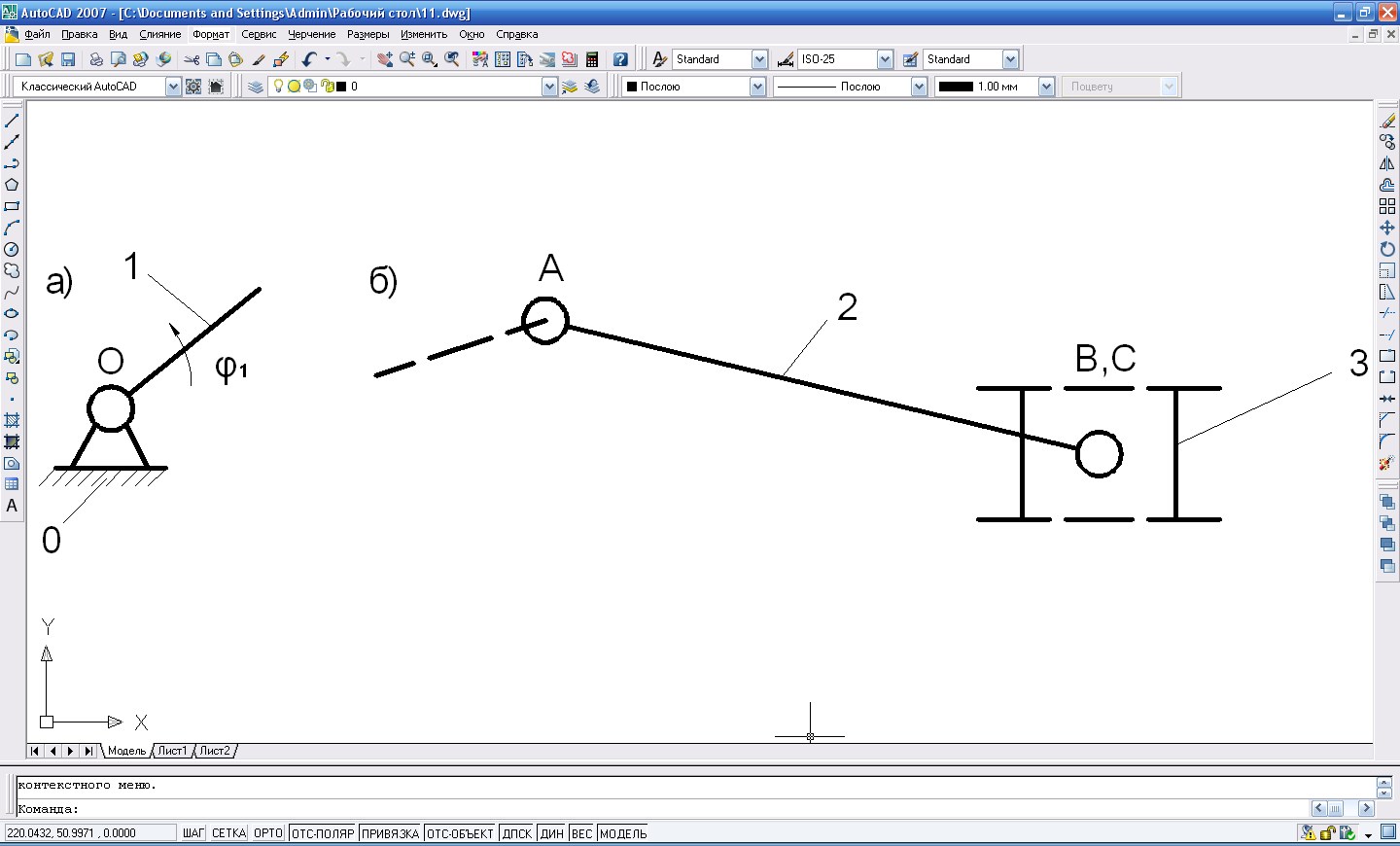
а) механизм 1 класса; б) группа Ассура 2 класса, 2 порядка, 2 вида.

Рисунок 3.2. Структурный анализ.

Так как наивысший класс присоединенной группы Ассура – второй, то

механизм относится ко второму классу.

Формула строения механизма:

3. Определение геометрических размеров рычажного механизма.

Исходные данные:

ход поршня H=0,124м;

частота вращения карданного вала n₁=2050об/мин;

максимальный угол давления между шатуном и поршнем =12,5⁰;

диаметр поршня d=0,084м;

частота вращения карданного вала =180 об/мин.

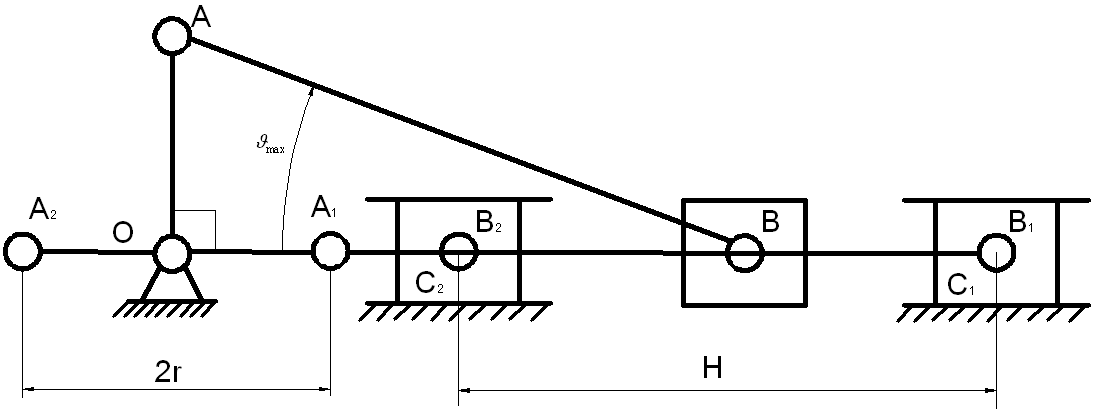
Рисунок 3.3. Положения механизма в крайних точках и при максимальном угле давления.

На Рисунке 3.3. изображен механизм в крайних положениях с указанием хода поршня – H, и положение механизма при котором имеет максимальное значение угол давления.

Найдем длину кривошипа:

где - длина кривошипа; Н- ход поршня.

м.

Найдем длину шатуна из отношения при максимальном угле давления:

.

где - максимальный угол давления шатуна ; - длина шатуна.

м.

Положение центров масс звеньев механизма:

Так как кривошип уравновешен, то центр масс лежит в точке О - .

Центр масс шатуна находится в точке на линии АВ:

где - расстояние от точки А до центра масс шатуна.

м.

Центр масс ползуна находится в точке В - .

Массы звеньев:

m₂=q l_АВ

где q- масса одного метра звена; m₂- масса шатуна.

m₂= кг.

m₃=0,8 m₂

где m₃-масса поршня.

m₃= кг.

m₁=3,8 m₂

где m₁- масса кривошипа.

m₁= кг.

Осевые моменты инерции звеньев:

где - осевой момент инерции шатуна.

кгм².

где - осевой момент инерции кривошипа.

кгм².

Средняя угловая скорость кривошипа определяется по формуле:

_1ср=

где - средняя угловая скорость кривошипа.

Таблица 3.1. Результаты расчета геометрических характеристик механизма.

1ср, 1/c	Размеры l,м			Массы,кг			Осевые моментыинерции Is, кгм2
	lОА	lАВ	lAS2	m1	m2	m3
-214,676	0,062	0,287	0,095	9,8	2,6	2,1	0,019	0,038

4. Расчет кинематических характеристик рычажного механизма. Графический метод.

1. Построение планов положения механизма.

После завершения расчета геометрических размеров приступаем к построению планов положений механизма.

Для построения планов положений механизма необходимо определить масштабный коэффициент, используя который реальные размеры звеньев выражаются в отрезках, изображаемых на чертеже.

Для этого примем ОА=40 мм, тогда

где - масштабный коэффициент; ОА-отрезок на чертеже эквивалентный . м/мм.

Примем масштабный коэффициент =0,001 м/мм.

Определим величины OA,АВ и АS₂:

Где OA-отрезок на чертеже равный .

где АВ - отрезок на чертеже равный .

мм.

где АS₂ - отрезок на чертеже равный .

мм.

Для построения плана положений необходимо выбрать точку О и провести окружность радиусом ОА. Разбиваем окружность на 12 равных частей( ).

Нумеруем полученные точки и соединяем их с центром О. Полученные точки являются планом положений кривошипа.

Из построенных на окружности точек проводим отрезки длиной АВ до пересечения их с осью ОХ. Полученные точки нумеруем в соответствии с нумерацией точек на окружности. Полученные точки являются планом положений ползуна, а отрезки - шатуна.

На плане положений шатуна от точек А_i откладываем отрезки длиной АS _i, и полученные точки нумеруем соответственно точкам на окружности. Данные точки будут являться положениями центра массы шатуна.

Выполняем замеры и пересчет контрольных параметров:

- угол положения шатуна φ₂=349 ;

- координата ползуна х_B= м;

- координаты центра масс шатуна x_S2= м, y_S2= м;

- перемещение ползуна SB= м.