
- •Часть 3
- •Часть 3
- •1. Элементы высшей алгебры
- •1.1. Комплексные числа
- •Тригонометрическая и показательная форма записи комплексных чисел.
- •1.2. Многочлены.
- •1.3. Рациональные дроби
- •2. Неопределенный интеграл
- •2.1. Первообразная и неопределенный интеграл
- •2.2. Интегрирование по частям
- •2.3. Метод замены переменной (метод подстановки).
- •2.4. Интегрирование рациональных дробей
- •2.5. Интегрирование выражений, содержащих тригонометрические функции.
- •3. Определенный интеграл
- •3.1. Определение определенного интеграла и его свойства.
- •3.2. Формула Ньютона-Лейбница.
- •3.3. Методы вычисления определенных интегралов.
- •3.3.1. Метод замены переменной (метод подстановки).
- •3.3.2. Интегрирование по частям
- •3.4. Несобственные интегралы
- •3.5. Геометрические и механические приложения определенного интеграла.
- •5. Статистические моменты и координаты центра масс плоской фигуры
- •4. Задания для контрольных и расчетно-графических работ.
- •5. Ответы на задания для контрольных и расчетно-графических работ
- •Список литературы
2.5. Интегрирование выражений, содержащих тригонометрические функции.
Пусть
![]() - рациональная функция своих аргументов
и
,
т.е. над
и
совершаются только арифметические
операции. Например,
- рациональная функция своих аргументов
и
,
т.е. над
и
совершаются только арифметические
операции. Например,
![]() ;
;
 .
.
Функция
![]() не является рациональной.
не является рациональной.
Универсальная подстановка.
Интеграл вида
![]() с помощью подстановки
с помощью подстановки
![]() ,
которая называется универсальной,
всегда сводится к интегралу от рациональной
функции от переменной
.
,
которая называется универсальной,
всегда сводится к интегралу от рациональной
функции от переменной
.
Действительно,
 ,
,
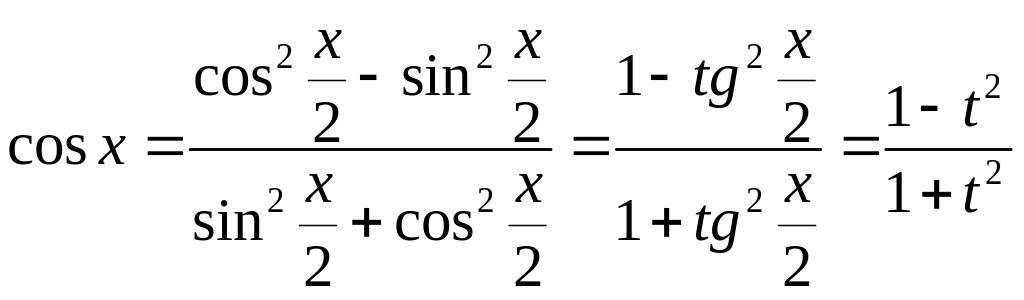 ,
,
![]() .
.
Поэтому
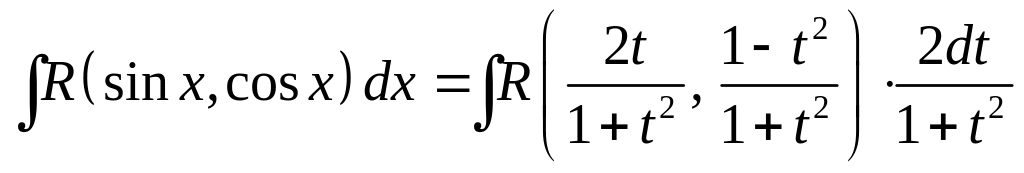 ,
т.е. получим интеграл от рациональной
функции по переменной
(т.е., как говорят, рационализируем
интеграл).
,
т.е. получим интеграл от рациональной
функции по переменной
(т.е., как говорят, рационализируем
интеграл).
Пример 2.7.
Найти
![]() ,
применив универсальную подстановку.
,
применив универсальную подстановку.
Решение.
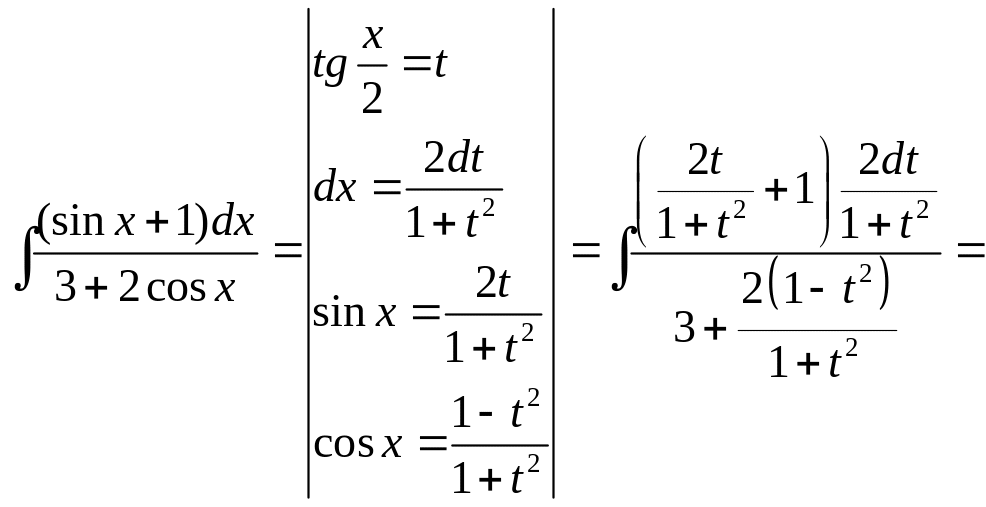
 .
.
Р
![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ).
).
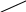

 .
.
Приравниваем числители:
![]() .
.
Приведем подобные в правой части равенства:
![]() .
.
Для определения
коэффициентов
![]() применим метод приравнивания коэффициентов
при одинаковых степенях
:
применим метод приравнивания коэффициентов
при одинаковых степенях
:
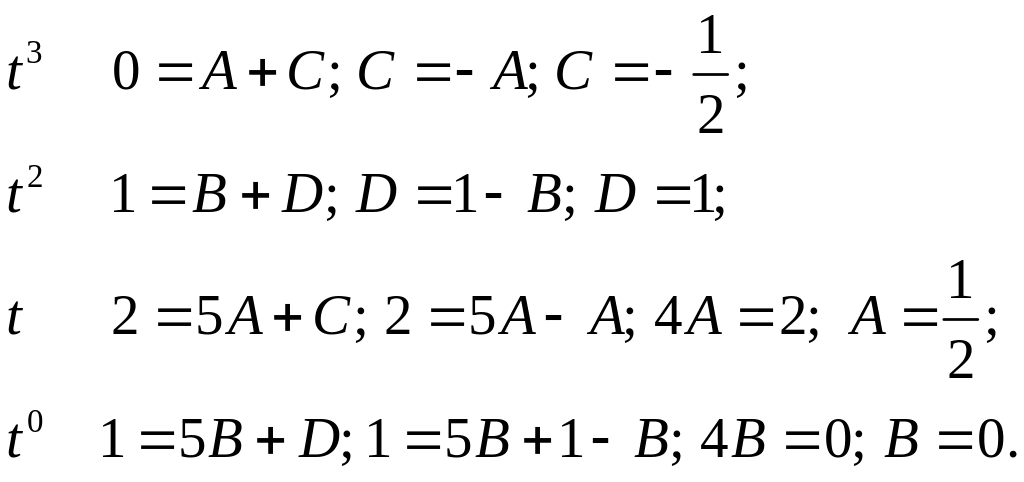

Заметим, что
полученная система четырех уравнений
распалась на две системы двух уравнений
 и
и
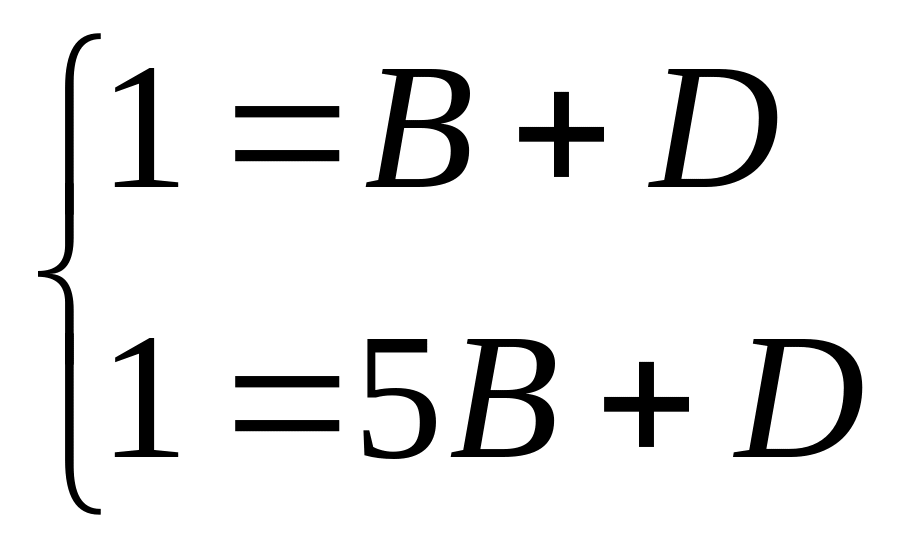 ,
которые и были решены.
,
которые и были решены.
Учитывая полученные результаты для , можно записать:


![]()
![]()
![]()
![]() .
.
Вспомогательные вычисления:
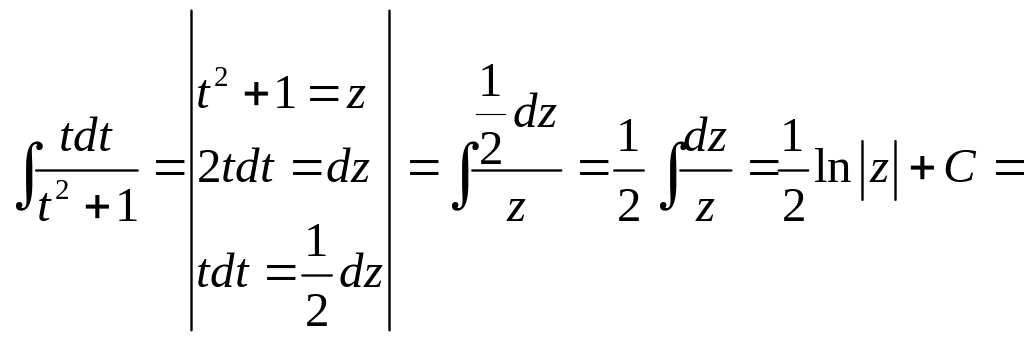
![]() .
.
Аналогично находится
![]() .
.
Таким образом,
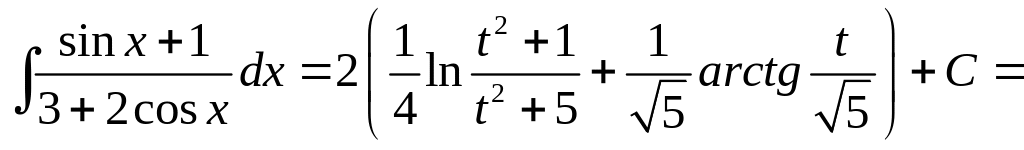
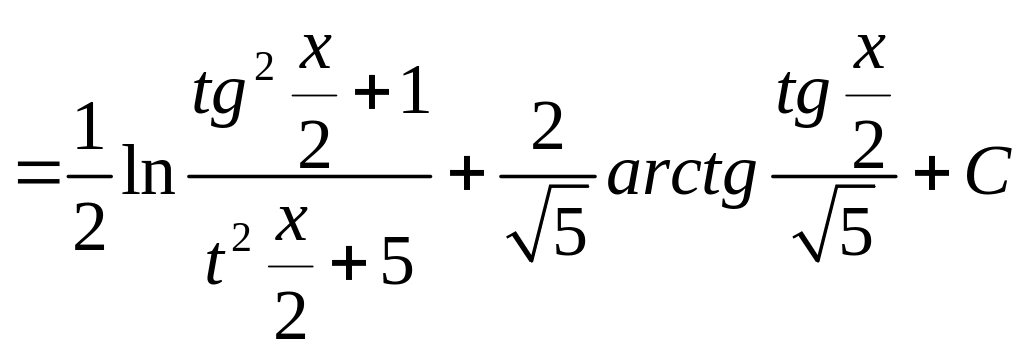 .
.
Применение универсальной подстановки, как правило, приводит к громоздким вычислениям, о чем свидетельствует и решение примера (2.7). Поэтому ниже приведем частные случаи, когда интеграл можно рационализировать, не применяя универсальную подстановку, что упрощает вычисления.
1.
 .
.
2.
 .
.
3.
 .
.
4.
при условии, что
![]() и
и
![]() входят в подынтегральную функцию только
в четных степенях, рационализируется
также подстановкой
входят в подынтегральную функцию только
в четных степенях, рационализируется
также подстановкой
![]() ,
поскольку
,
поскольку
![]() ,
,
![]() .
.
5.
![]() рационализируется: подстановкой
рационализируется: подстановкой
![]() ,
если
-нечетное,
подстановкой
,
если
-нечетное,
подстановкой
![]() ,
если
,
если
![]() - нечетное; применением формул
- нечетное; применением формул
![]() ,
,
![]() ,
если
и
- неотрицательные четные числа; если
и
- четные числа, но хотя бы одно отрицательное,
то подстановкой
(случай 4).
,
если
и
- неотрицательные четные числа; если
и
- четные числа, но хотя бы одно отрицательное,
то подстановкой
(случай 4).
6.
![]() ,
,
![]() ,
,
![]() вычисляются применением формул
вычисляются применением формул
![]()
![]() ,
,
![]() ,
,
![]()
и таблицы интегралов.
► Представьте в
виде суммы (разности) выражения
![]() ,
,
![]() ,
,
![]() .
.
► Приведите примеры интегралов, которые соответствовали бы пунктам 1-6, и укажите подстановку, с помощью которой их можно рационализировать.
Пример 2.8. Найти интегралы от выражений, содержащих тригонометрические функции.
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Воспользуемся формулой
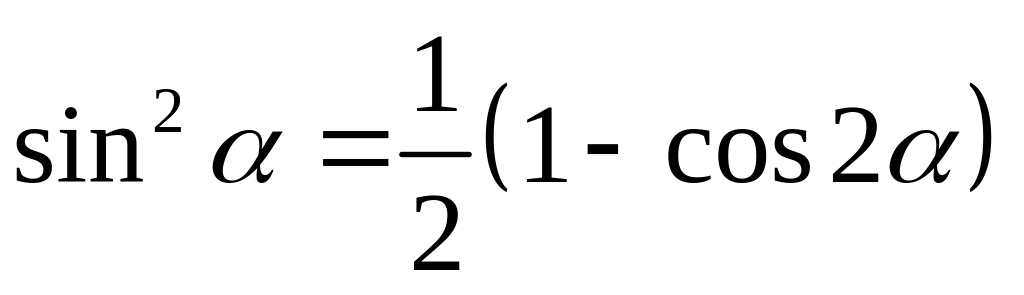 .
.
![]()
![]() .
.
В соответствии с формулой
,
![]()
![]() .
.
![]()
![]() .
.
3)
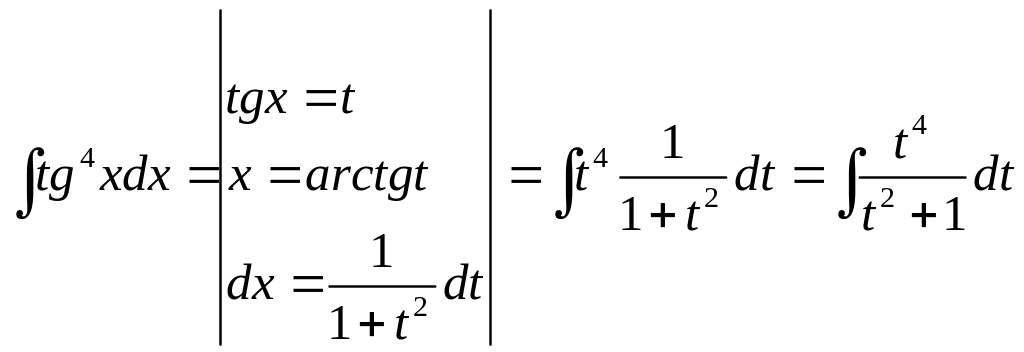 .
.
Получим интеграл от неправильной рациональной дроби. В данной ситуации выделить целую часть можно следующим образом:
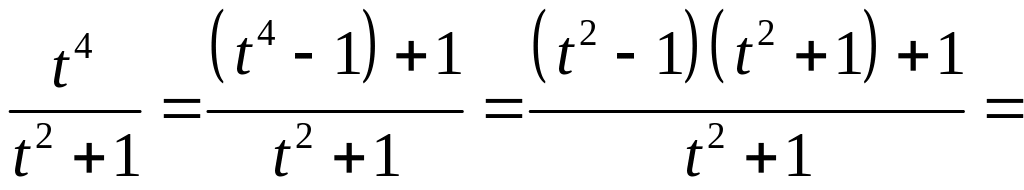
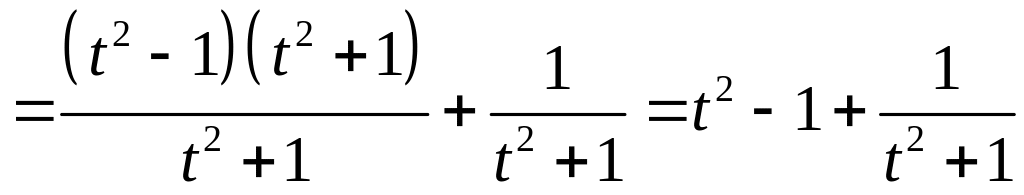 ,
,
![]()
![]() .
.
Следовательно,
![]()
![]() .
.
▶ Найти интегралы от выражений, содержащих тригонометрические функции.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В последнем
интеграле следует применить подстановку
![]() ,
,
![]() ,
,
![]() .
.
Ответы: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
3. Определенный интеграл
3.1. Определение определенного интеграла и его свойства.
Пусть на отрезке
![]() задана ограниченная функция
.
Разделим отрезок
произвольным образом на
частей
задана ограниченная функция
.
Разделим отрезок
произвольным образом на
частей
![]() точками
точками
![]()
![]() .
На каждом частичном отрезке
.
На каждом частичном отрезке
![]() разбиения выберем произвольную точку
разбиения выберем произвольную точку
![]() ,
вычислим в ней значение функции
,
вычислим в ней значение функции
![]() ,
умножим его на длину отрезка
,
умножим его на длину отрезка
![]() и составим сумму
и составим сумму
![]() ,
,
которую называют интегральной сумой функции , соответствующей выбранному разбиению.
Предел, к которому
стремится интегральная сумма
![]() ,
когда максимальная из длин частичных
отрезков стремится к нулю, если он
существует и не зависит ни от способа
разбиения отрезка
,
ни от выбора точек
,
когда максимальная из длин частичных
отрезков стремится к нулю, если он
существует и не зависит ни от способа
разбиения отрезка
,
ни от выбора точек
![]() ,
называется определенным интегралом от
функции
на отрезке
и обозначается символом
,
называется определенным интегралом от
функции
на отрезке
и обозначается символом
 .
.
Таким образом, по определению
 (3.1)
(3.1)
Число называется нижним пределом, а - верхним пределом определенного интеграла; отрезок называется отрезком интегрирования, - переменной интегрирования.
Если для функции предел (3.1) существует, то она называется интегрируемой на отрезке .
Имеет место утверждение: если функция непрерывна на отрезке , то она интегрируема на этом отрезке.
Г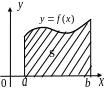 еометрический
смысл определенного интеграла: если
еометрический
смысл определенного интеграла: если
![]() на отрезке
,
то
численно равен площади криволинейной
трапеции, ограниченной кривой
,
прямыми
на отрезке
,
то
численно равен площади криволинейной
трапеции, ограниченной кривой
,
прямыми
![]() и осью
(рис.3.1):
и осью
(рис.3.1):
.

Рис. 3.1.
Отметим, что, по определению,
1)
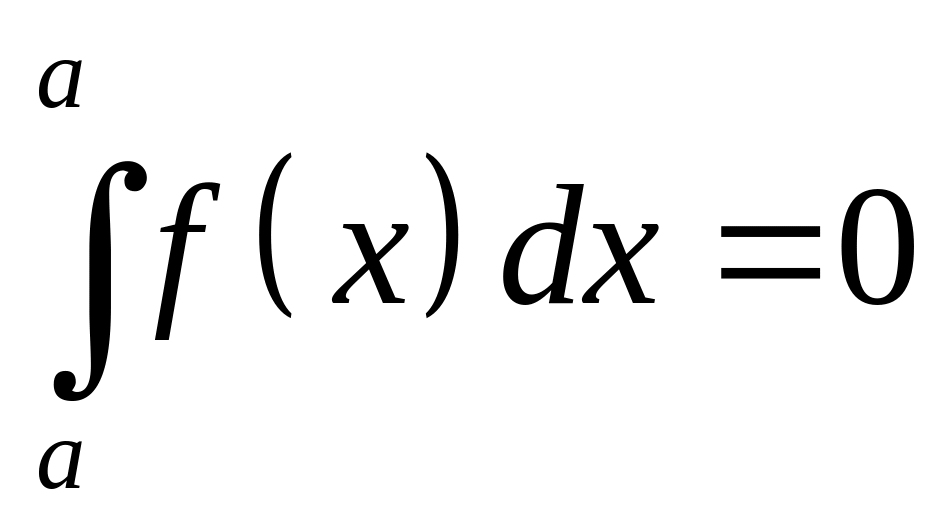 ;
2)
;
2)
 . (3.2)
. (3.2)
Приведем без доказательства основные свойства определенного интеграла, часть из которых проиллюстрируем графически, пользуясь геометрическим смыслом определенного интеграла.
Постоянный множитель можно выносить за знак определенного интеграла
 .
.
Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от слагаемых функций.


 .
.
Если на отрезке , где
 ,
функции
и
,
функции
и
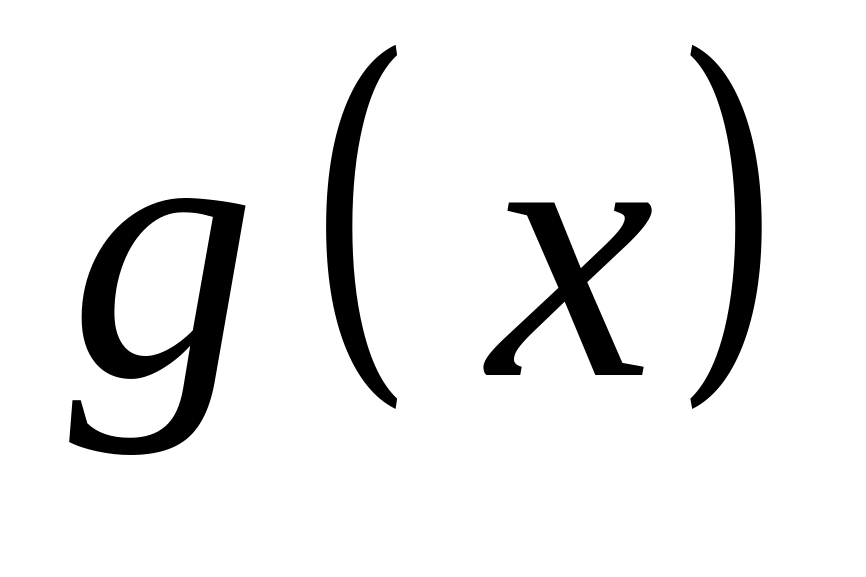 удовлетворяют условию
удовлетворяют условию
![]() ,
то
,
то
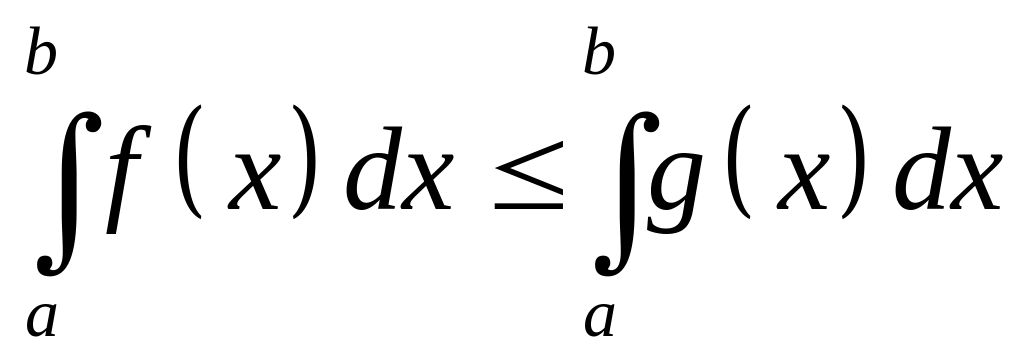
0

Рис.3.3.
Если и
 - наименьшее и наибольшее значения
функции
на отрезке
и
,
то
- наименьшее и наибольшее значения
функции
на отрезке
и
,
то

Если функция непрерывна на отрезке , то на этом отрезке существует такая точка
 ,
что справедливо равенство
,
что справедливо равенство
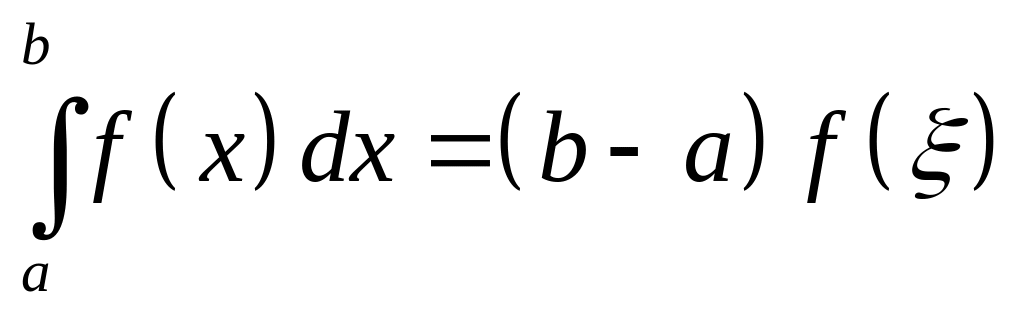
![]()


Рис.3.4.
6





 .
Если функция
интегрируема на каждом из отрезков
.
Если функция
интегрируема на каждом из отрезков
![]() и
и
![]() ,
то она интегрируема и на отрезке
и
,
то она интегрируема и на отрезке
и
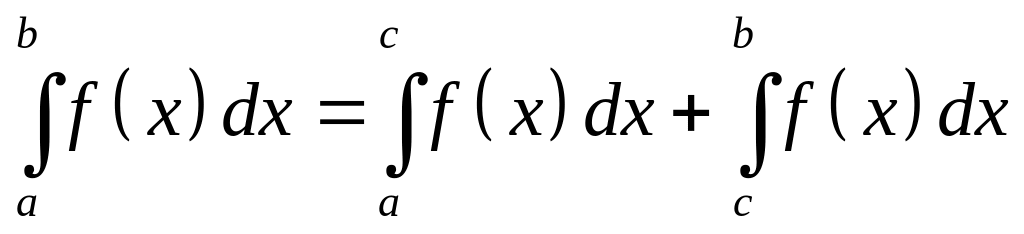
 Рис.3.5.
Рис.3.5.
Если подынтегральная функция четная (
 )
на отрезке интегрирования
)
на отрезке интегрирования
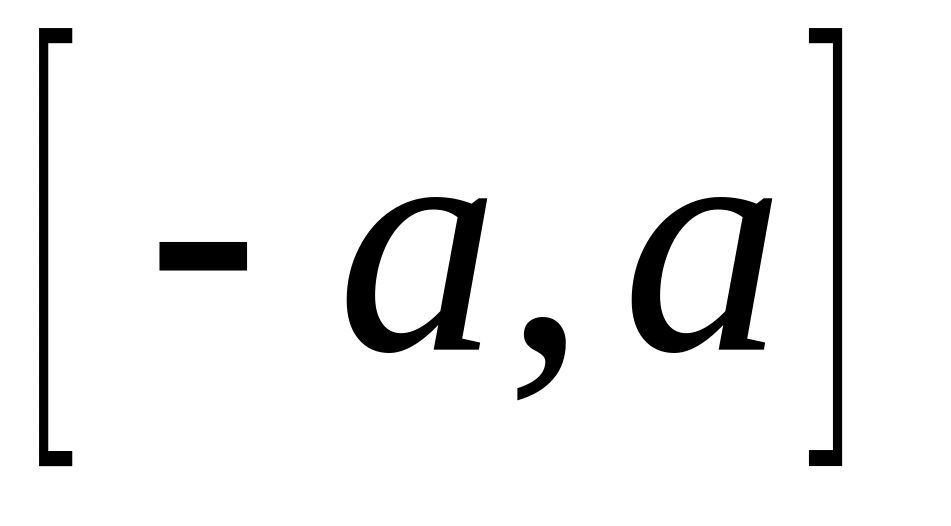 ,
то
,
то
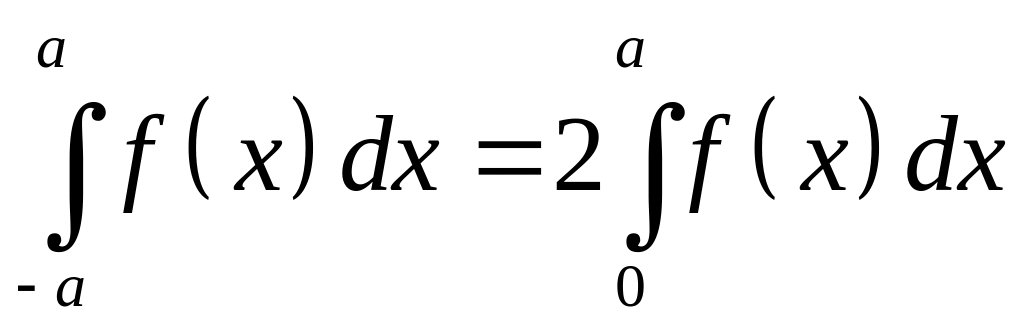 .
.

Рис.3.6.
8. Если подынтегральная
функция
нечетная (![]() )
на отрезке интегрирования
,
то
)
на отрезке интегрирования
,
то
 .
.

Рис.3.7.
9. Если подынтегральная
функция
- периодическая с периодом
![]() (
(![]() ),
то
),
то
 ,
т.е. для периодической с периодом
,
т.е. для периодической с периодом
![]() функции определенный интеграл дает
одно и то же значение при интегрировании
по любому отрезку длиной, равной
.
функции определенный интеграл дает
одно и то же значение при интегрировании
по любому отрезку длиной, равной
.
► Запишите формулировку свойств определенного интеграла, записанных формулами (3.2).
► Запишите свойство 2) определенного интеграла для случая трех слагаемых функций.
