2.2. Интегрирование по частям

Пусть и непрерывно дифференцируемые функции от . Тогда

.

Напомним: если , то дифференциал ; поэтому ; .

Тогда и .

Учитывая, что , получаем:

. (2.1)

Поскольку в равенстве (2.1 справа стоит неопределенный интеграл, который также содержит произвольную постоянную, то постоянную обычно опускают, и формулу интегрирования по частям записывают в виде

. (2.2)

Эта формула применяется чаще всего к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей и , чтобы нахождение функции по ее дифференциалу по формуле и вычисление составили в совокупности задачу более простую, чем непосредственное вычисление .

Укажем некоторые типы интегралов, которые находятся интегрированием по частям.

І. ; ; .

Здесь полагают , а остальное включают в , т.е. или или .

ІІ. ; ; .

Здесь полагают , а остальное включают в , т.е. или или .

ІІІ. ; .

Здесь не имеет значения, что принимать за , а что включать в .

В приведенных интегралах многочлен степени , т.е.

.

► Запишите формулу интегрирования по частям.

► Приведите примеры интегралов, которые относятся к І, ІІ, и ІІІ типу и укажите, что в них следует принять в качестве , а что включить в .

Пример 2.2. Найти неопределенные интегралы.

а) ; b) .

Решение:

а) интеграл относится к типу І, .

.

Замечание: при определении функции по ее дифференциалу по свойству 2 неопределенного интеграла следует добавлять постоянную , но т.к. в конечный результат она не входит (что легко проверить, подставив в равенстве (2.2) вместо выражение ), то удобно считать произвольную постоянную равной нулю;

b) второй интеграл относится к типу ІІ, .

.

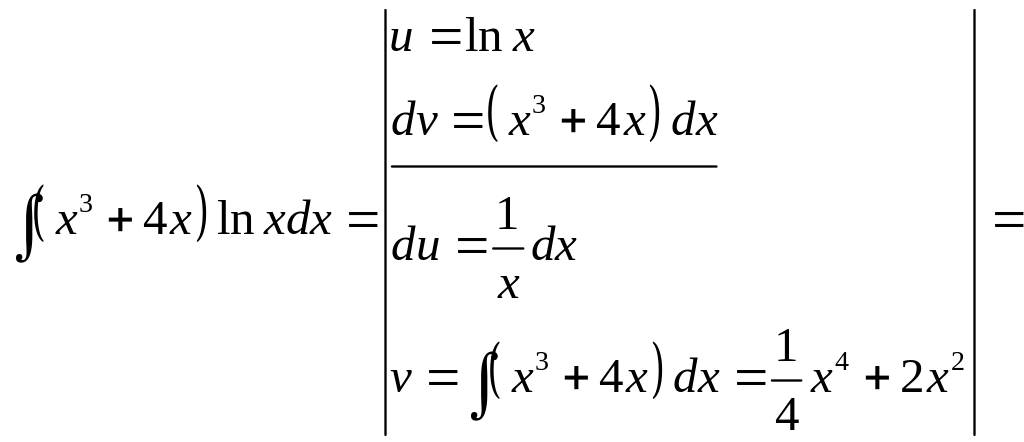
▶ Найти

Ответы: 1) ; 2) .

2.3. Метод замены переменной (метод подстановки).

Пусть требуется найти , причем непосредственным интегрированием это не удается .

Сделаем замену переменной в подинтегральном выражении, положив

, (2.3)

где - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда и справедливо равенство

. (2.4)

Подчеркнем, что после нахождения интеграла в (2.4) следует в полученный результат подставить вместо его выражение через , найденное из равенства (2.3).

Удачный выбор новой переменной существенно облегчает нахождение интеграла.

При этом помогут следующие соображения: если подынтегральное выражение содержит функции , , , , , , , , у которых вместо аргументом является , как правило, применяется подстановка . Если подынтегральное выражение содержит корни разных степеней из одного и того же выражения, то это выражение и принимается за новую переменную в такой степени, чтобы все корни «извлекались».

Пример 2.3. Найти интегралы

, , .

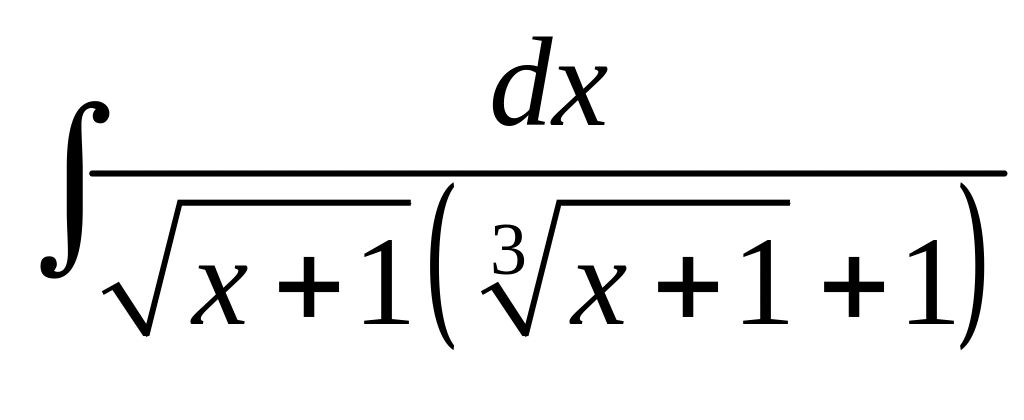Решение.

1)

;

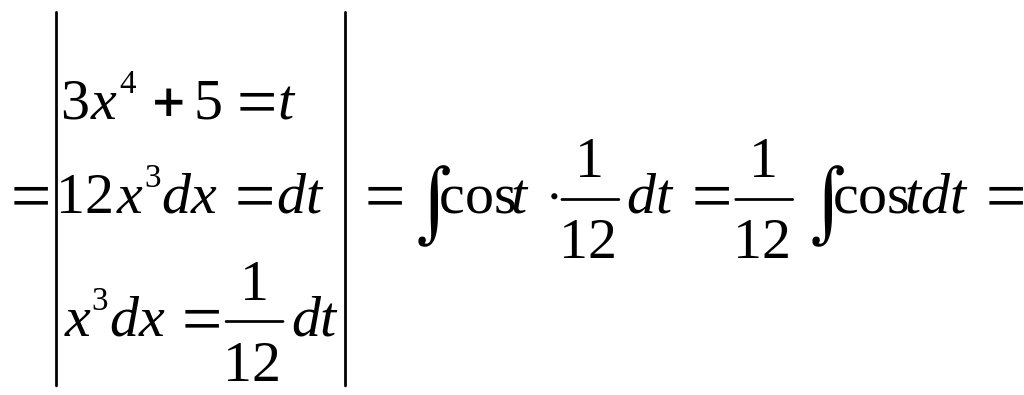
2)

;

3)

.

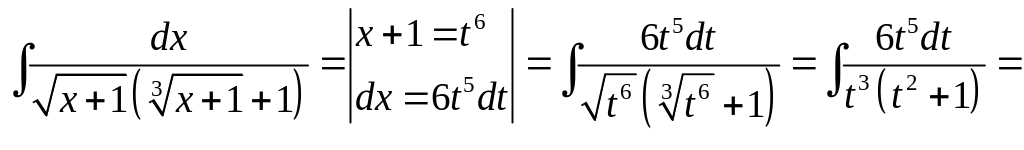
Метод замены переменной является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы применяем другой способ, часто в промежуточных вычислениях приходится применять метод подстановки.

Так, например, при вычислении интегралов от некоторых функций, содержащих квадратный трехчлен

,

сначала выделяют полный квадрат двучлена из квадратного трехчлена , т.е. представляют его в виде

,

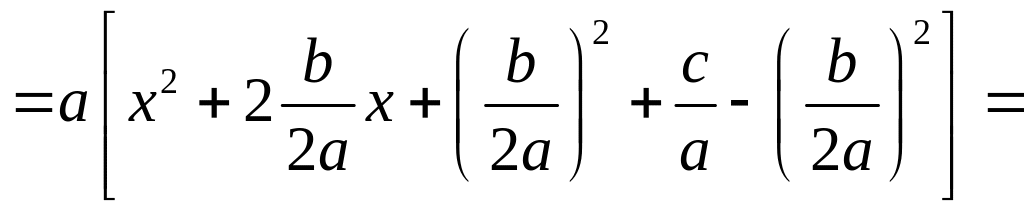
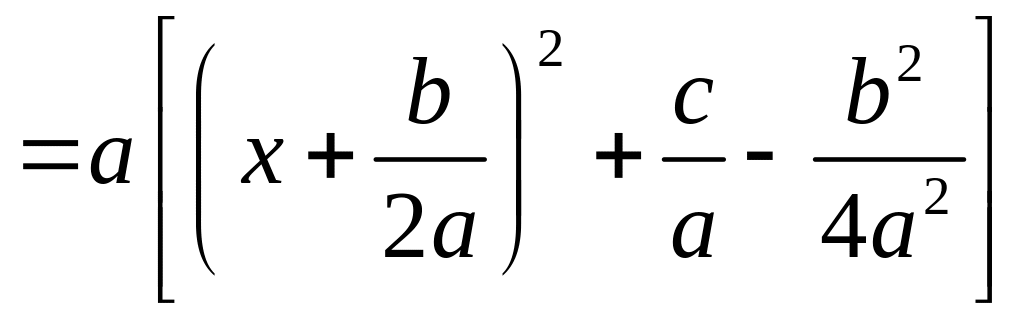а затем применяют подстановку .

Пример 2.4. Найти .

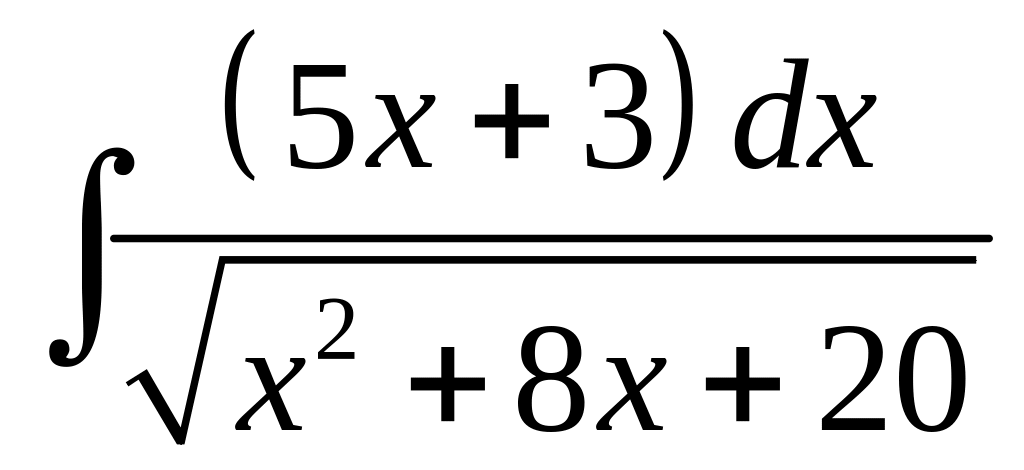Решение.

1. Выделим в квадратном трехчлене полный квадрат двучлена:

.

2. Применим подстановку .

.

Вычислим отдельно .

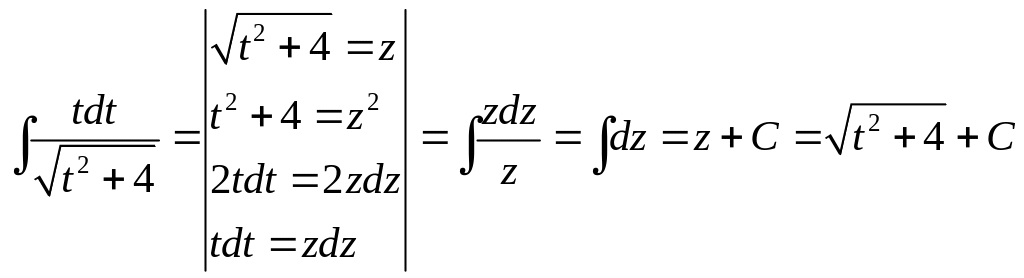► Какие формулы сокращенного умножения используются при выделении полного квадрата двучлена?

► Выделите полный квадрат из выражений:

а) ; б) , в) .

► Найти неопределенные интегралы.

а) ; b) .

Ответ: ; .