
- •Часть 3
- •Часть 3
- •1. Элементы высшей алгебры
- •1.1. Комплексные числа
- •Тригонометрическая и показательная форма записи комплексных чисел.
- •1.2. Многочлены.
- •1.3. Рациональные дроби
- •2. Неопределенный интеграл
- •2.1. Первообразная и неопределенный интеграл
- •2.2. Интегрирование по частям
- •2.3. Метод замены переменной (метод подстановки).
- •2.4. Интегрирование рациональных дробей
- •2.5. Интегрирование выражений, содержащих тригонометрические функции.
- •3. Определенный интеграл
- •3.1. Определение определенного интеграла и его свойства.
- •3.2. Формула Ньютона-Лейбница.
- •3.3. Методы вычисления определенных интегралов.
- •3.3.1. Метод замены переменной (метод подстановки).
- •3.3.2. Интегрирование по частям
- •3.4. Несобственные интегралы
- •3.5. Геометрические и механические приложения определенного интеграла.
- •5. Статистические моменты и координаты центра масс плоской фигуры
- •4. Задания для контрольных и расчетно-графических работ.
- •5. Ответы на задания для контрольных и расчетно-графических работ
- •Список литературы
5. Статистические моменты и координаты центра масс плоской фигуры
Напомним, что
статистические моменты материальной
точки с массой
,
помещенной в точку
![]() ,
относительно оси
и оси
,
относительно оси
и оси
![]() равны соответственно произведениям
равны соответственно произведениям
![]() и
и
![]() .
.
Рассмотрим
материальную плоскую фигуру (пластинку),
ограниченную линиями
,
,
,
,
![]() .
Поверхностную плотность фигуры, т.е.
массу единицы площади поверхности
фигуры будем считать постоянной и равной
.
Поверхностную плотность фигуры, т.е.
массу единицы площади поверхности
фигуры будем считать постоянной и равной
![]() .
Такая пластика называется однородной.
Тогда масса
этой пластики вычисляется по формуле
.
Такая пластика называется однородной.
Тогда масса
этой пластики вычисляется по формуле
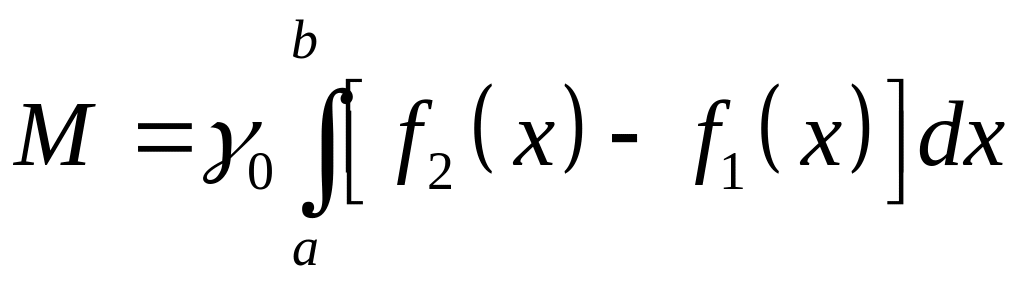 ,
(3.17)
,
(3.17)
а ее статистические моменты относительно осей координат по формулам
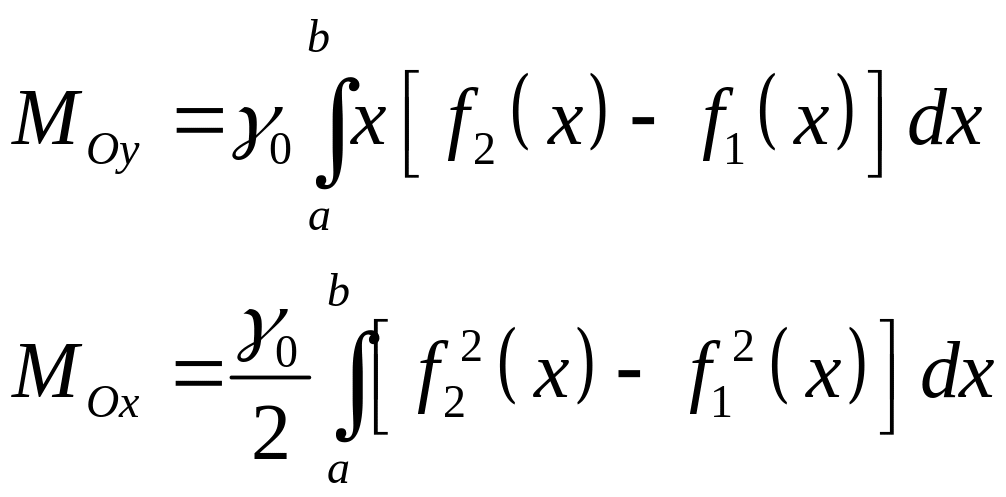 ,.
(3.18)
,.
(3.18)
Центром масс
пластинки называется такая ее точка
![]() ,
для которой
,
для которой
![]() ;
;
![]() .
.
Отсюда, с учетом равенства (3.17) и (3.18), получаем формулы, по которым вычисляются координаты центра масс однородной пластинки:
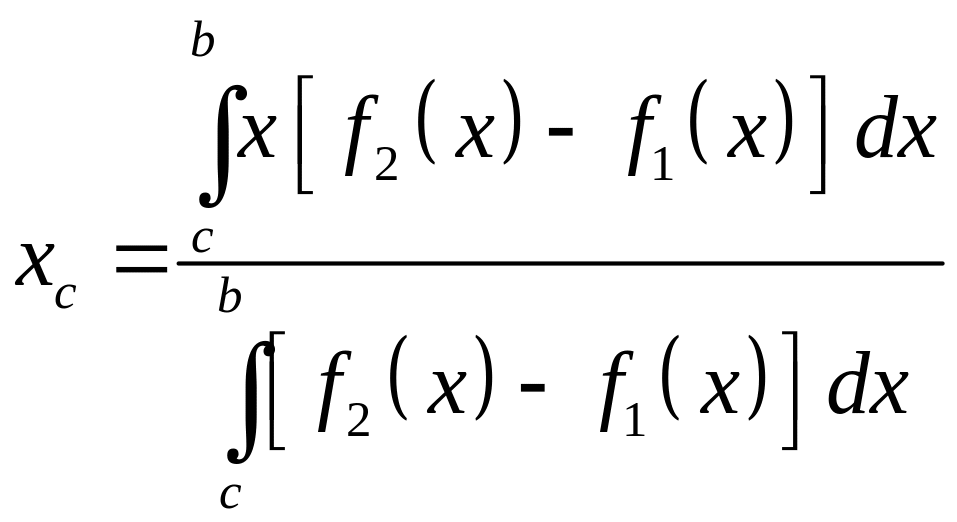 ,
,
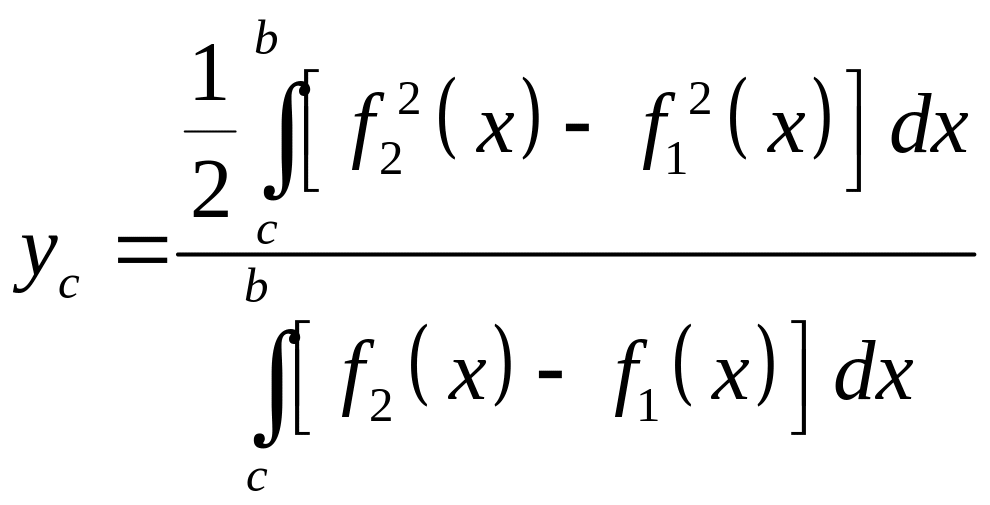 .
(3.19)
.
(3.19)
► Перечислите механические приложения определенного интеграла и укажите соответствующие формулы.
Пример 3.10.Найти
координаты центра масс однородной
пластинки, ограниченной линиями
![]() ,
.
,
.
Решение. Для решения задачи воспользуемся формулами (3.19), в которых положим
![]() .
.
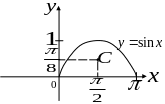
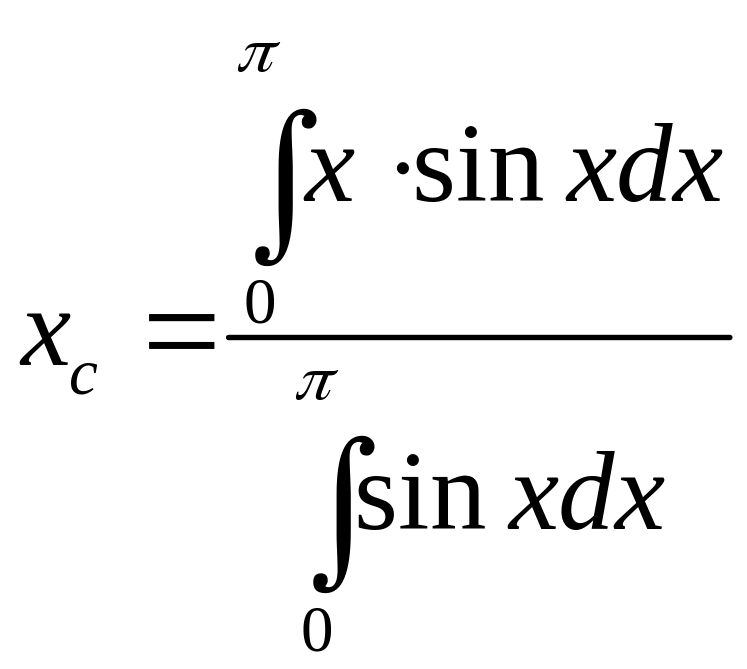 ,
,
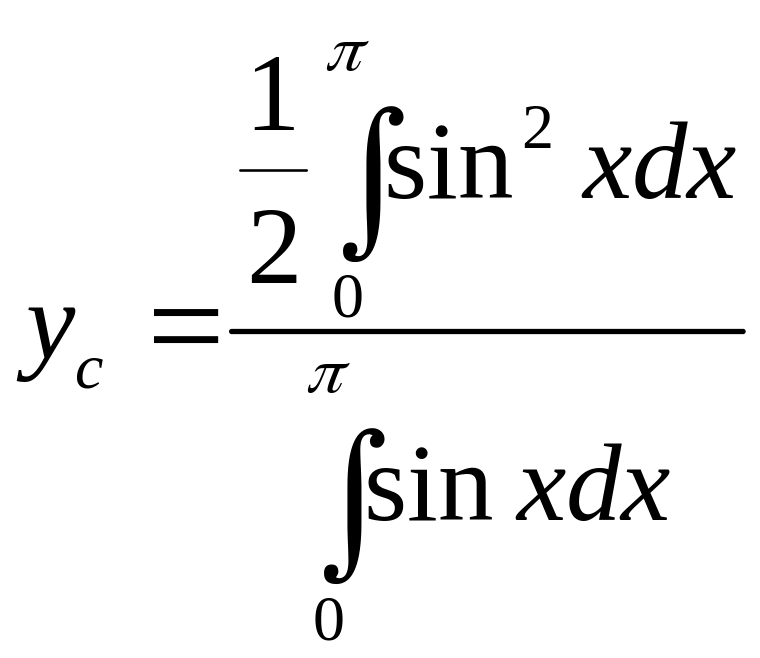 .
.
Вспомогательные вычисления.
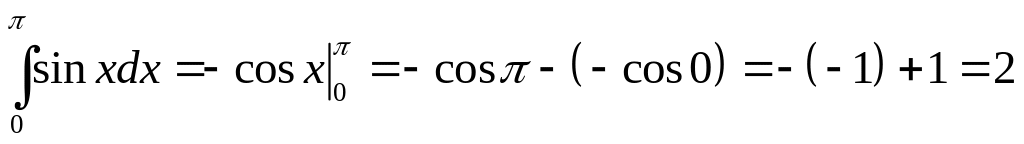 ,
,
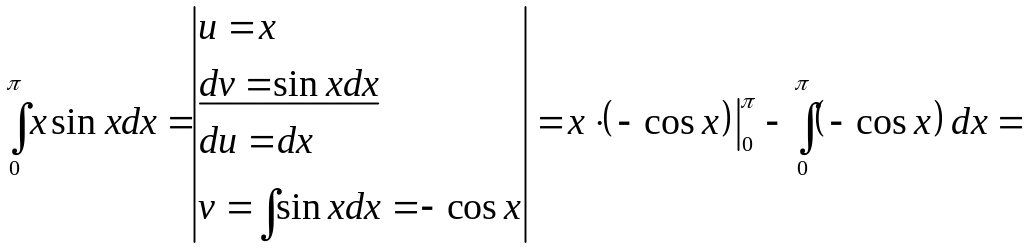
![]() ,
,
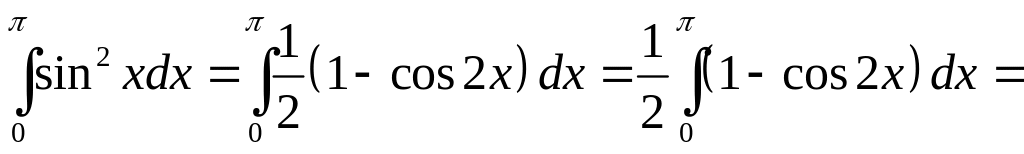
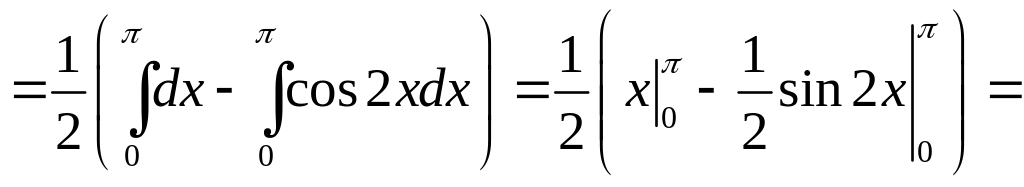
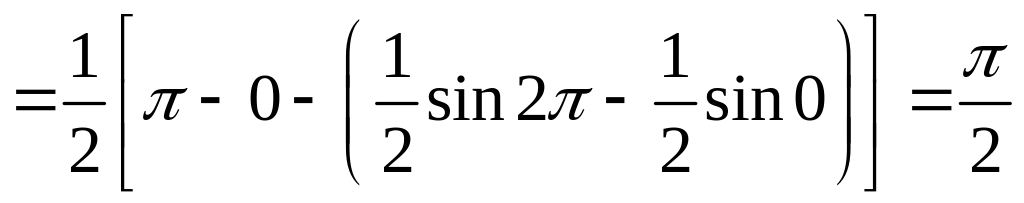 .
.
Используя эти результаты, получим:
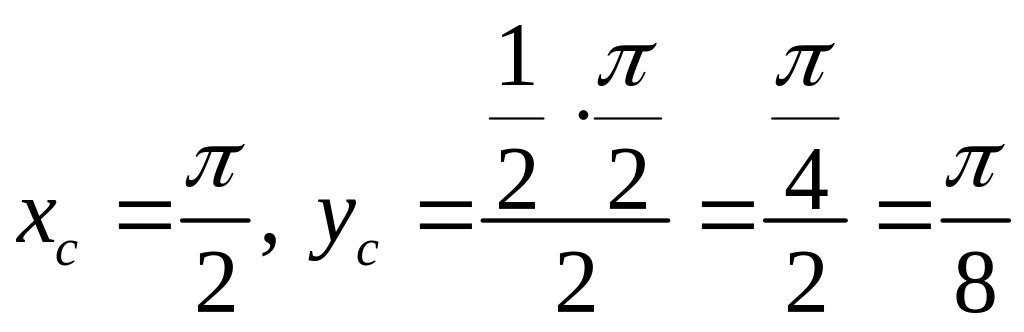 .
.
4. Задания для контрольных и расчетно-графических работ.
I. Решить уравнение. Сделать проверку. Изобразить корни уравнения на комплексной плоскости.
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29. |
2.
4.
6.
8.
10.
12. 14.
16.
18.
20.
22.
24.
26.
28.
30.
|
II. Даны числа
![]() .
Найти:
.
Найти:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() найти, используя
тригонометрическую и показательную
формы числа
найти, используя
тригонометрическую и показательную
формы числа
![]() .
.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]()
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]()
25.
![]()
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
III. Решить уравнение, считая и действительными числами. Сделать проверку.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]()
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]()
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
IV. Разложить многочлен на простейшие множители с действительными коэффициентами.
1. а)
![]() ;
б)
;
б)
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() .
.
3. а)
![]() ;
б)
;
б)
![]() .
.
4. а)
![]() ;
б)
;
б)
![]() .
.
5. а)
![]() ;
б)
;
б)
![]() .
.
6. а)
![]() ;
б)
.
;
б)
.
7. а)
![]() ;
б)
;
б)
![]() .
.
8. а)
![]() ;
б)
;
б)
![]() .
.
9. а)
![]() ;
б)
;
б)
![]() .
.
10. а)
![]() ;
б)
;
б)
![]() .
.
11. а)
![]() ;
б)
;
б)
![]() .
.
12. а)
![]() ;
б)
;
б)
![]() .
.
13. а)
![]() ;
б)
;
б)
![]() .
.
14. а)
![]() ;
б)
;
б)
![]() .
.
15. а)
![]() ;
б)
;
б)
![]() .
.
16. а)
![]() ;
б)
;
б)
![]() .
.
17. а)
![]() ;
б)
;
б)
![]() .
.
18. а)
![]() ;
б)
;
б)
![]() .
.
19. а)
![]() ;
б)
;
б)
![]() .
.
20. а)
![]() ;
б)
;
б)
![]() .
.
21. а)
![]() ;
б)
;
б)
![]() .
.
22. а)
![]() ;
б)
;
б)
![]() .
.
23. а)
![]() ;
б)
;
б)
![]() .
.
24. а)
![]() ;
б)
;
б)
![]() .
.
25. а)
![]() ;
б)
;
б)
![]() .
.
26. а)
;
б)
![]() .
.
27. а)
![]() ;
б)
;
б)
![]() .
.
28. а)
![]() ;
б)
;
б)
![]() .
.
29. а)
![]() ;
б)
;
б)
![]() .
.
30. а)
![]() ;
б)
;
б)
![]() .
.
V. Найти неопределенные интегралы.
В каждом случае записать табличный интеграл и значения входящих в него параметров.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
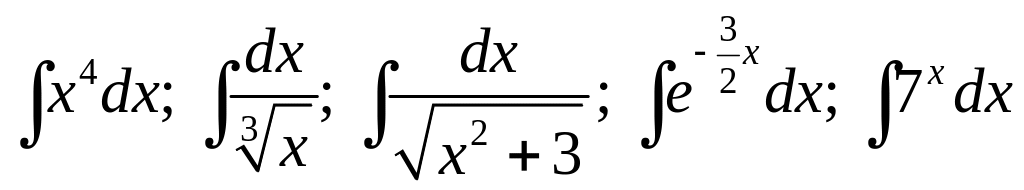 .
.
6.
![]() .
.
7.
![]() .
.
8.
![]()
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
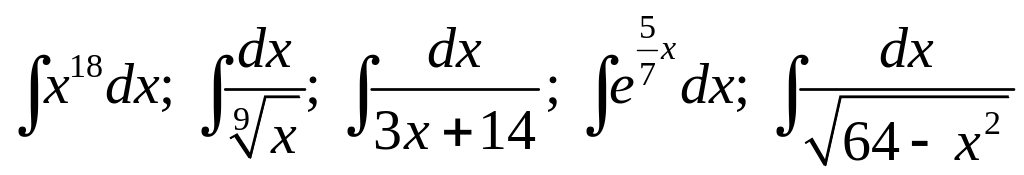 .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
VI. Найти неопределенные интегралы, пользуясь методом подстановки или применяя интегрирование по частям.
1. а)
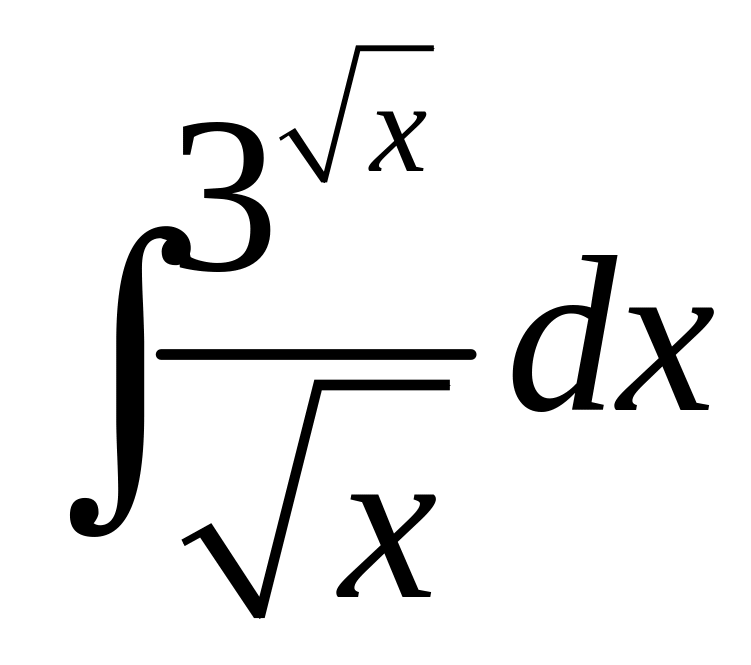 ; б)
; б)
![]() .
.
2. а)
![]() ; б)
; б)
![]() .
.
3. а)
![]() ; б)
; б)
![]() .
.
4. а)
![]() ; б)
; б)
![]() .
.
5. а)
![]() ; б)
; б)
![]() .
.
6. а)
![]() ; б)
; б)
![]() .
.
7. а)
![]() ; б)
; б)
![]() .
.
8. а)
![]() ; б)
; б)
![]() .
.
9. а)
![]() ;
б)
;
б)
![]() .
.
10. а)
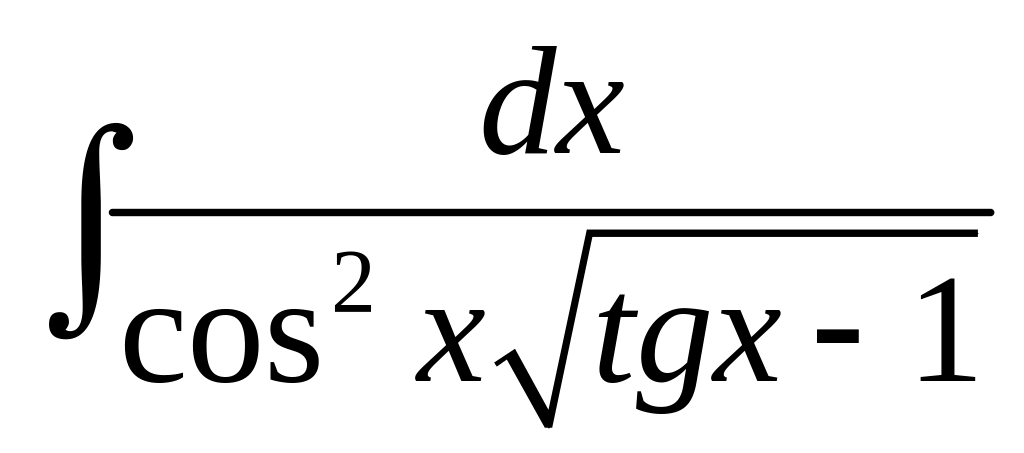 ;
б)
;
б)
![]() .
.
11. а)
![]() ; б)
; б)
![]() .
.
12. а)
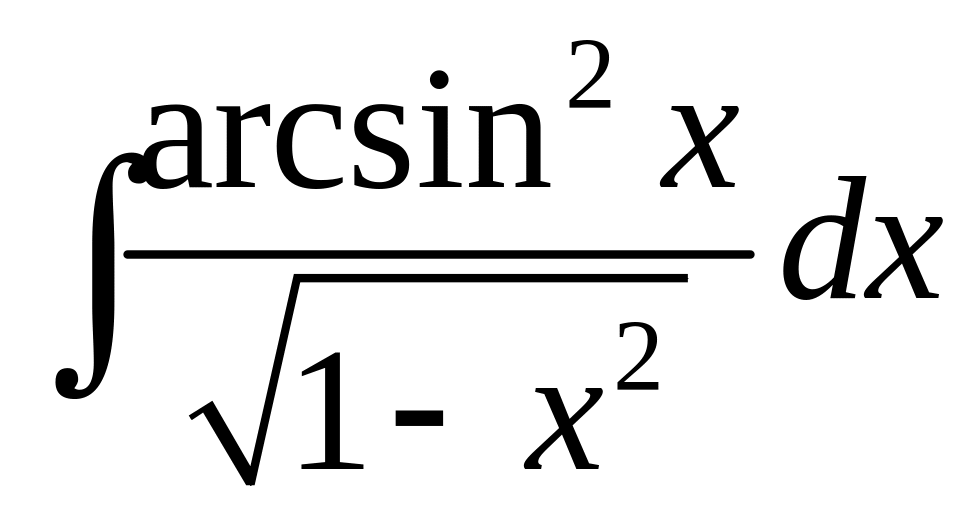 ; б)
; б)
![]() .
.
13. а)
![]() ; б)
; б)
![]() .
.
14. а)
![]() ; б)
; б)
![]() .
.
15. а)
![]() ; б)
; б)
![]() .
.
16. а)
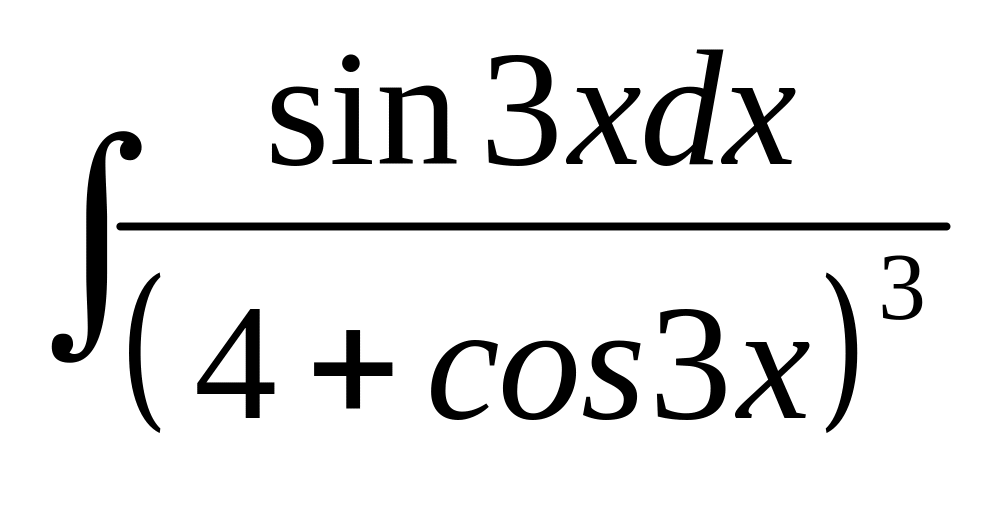 ; б)
; б)
![]() .
.
17. а)
![]() ; б)
; б)
![]() .
.
18. а)
![]() ; б)
; б)
![]() .
.
19. а)
![]() ; б)
; б)
![]() .
.
20. а)
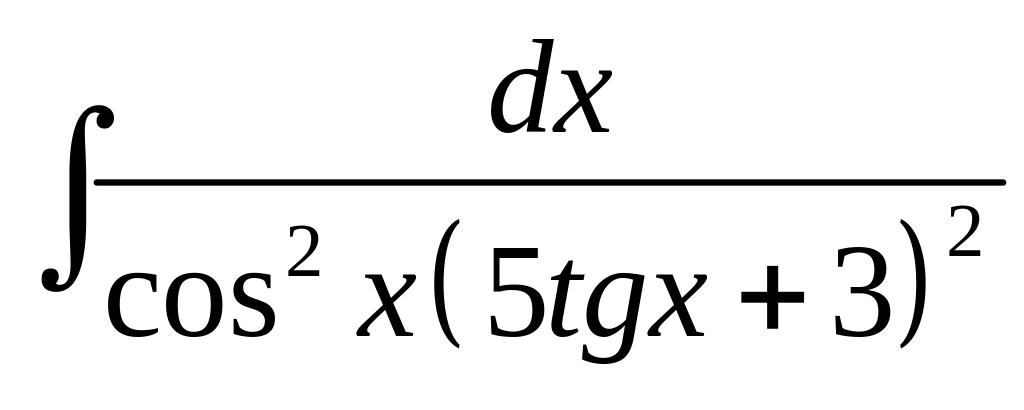 ; б)
; б)
![]() .
.
21. а)
![]() ; б)
; б)
![]() .
.
22. а)
![]() ; б)
; б)
![]() .
.
23. а)
![]() ; б)
; б)
![]() .
.
24. а)
![]() ; б)
; б)
![]() .
.
25. а)
![]() ; б)
; б)
![]() .
.
26. а)
![]() ; б)
; б)
![]() .
.
27. а)
![]() ; б)
; б)
![]() .
.
28. а)
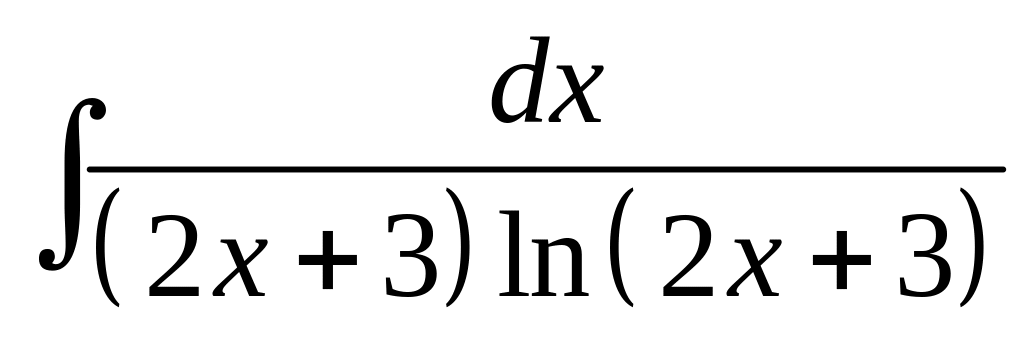 ; б)
; б)
![]() .
.
29. а)
![]() ; б)
; б)
![]() .
.
30. а)
![]() ; б)
.
; б)
.
VII. Найти интегралы от рациональных дробей.
1. а)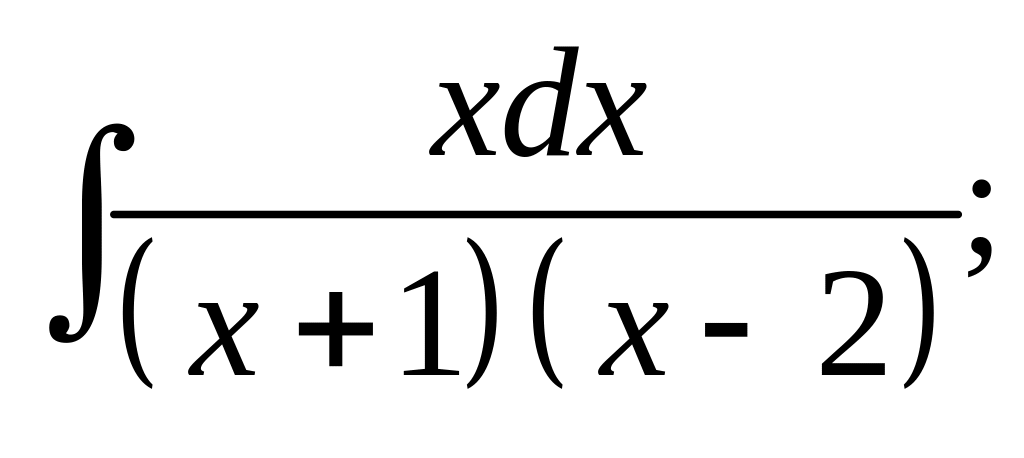 б)
б)
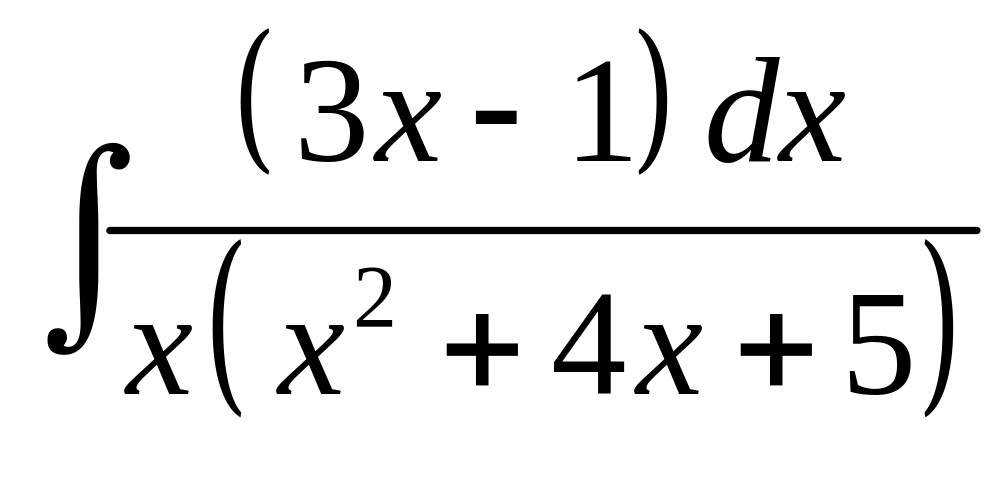 .
.
2. а)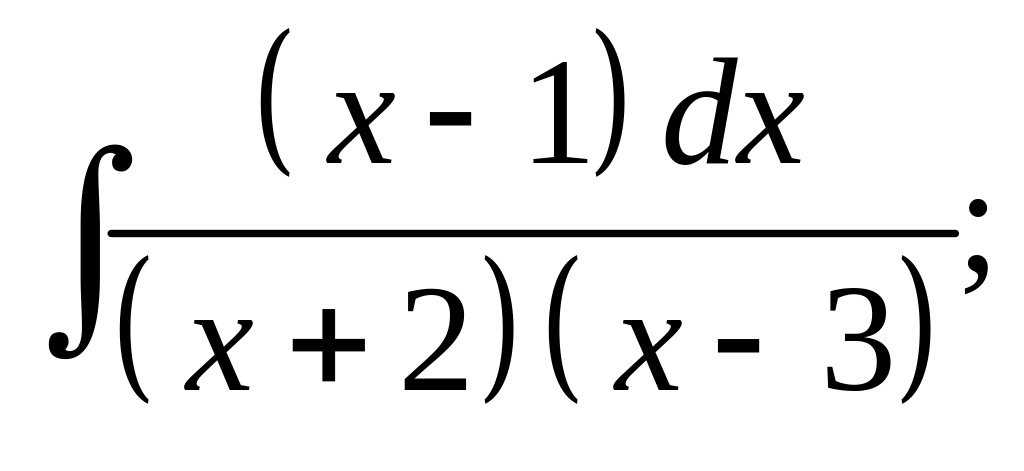 б)
б)
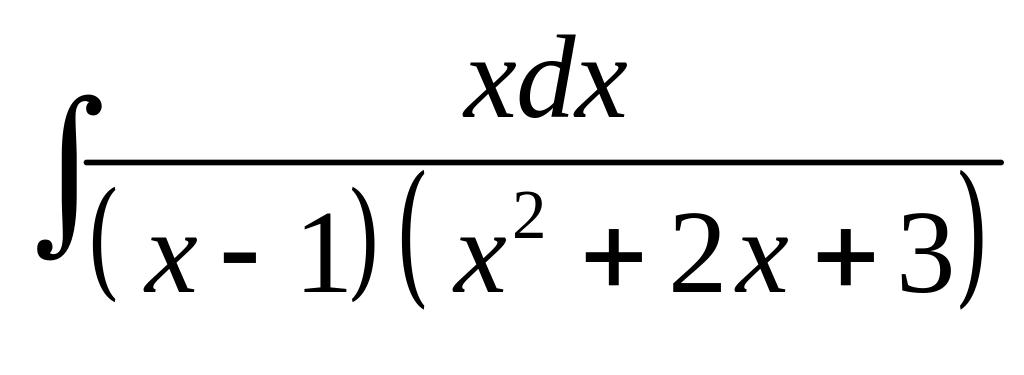 .
.
3. а)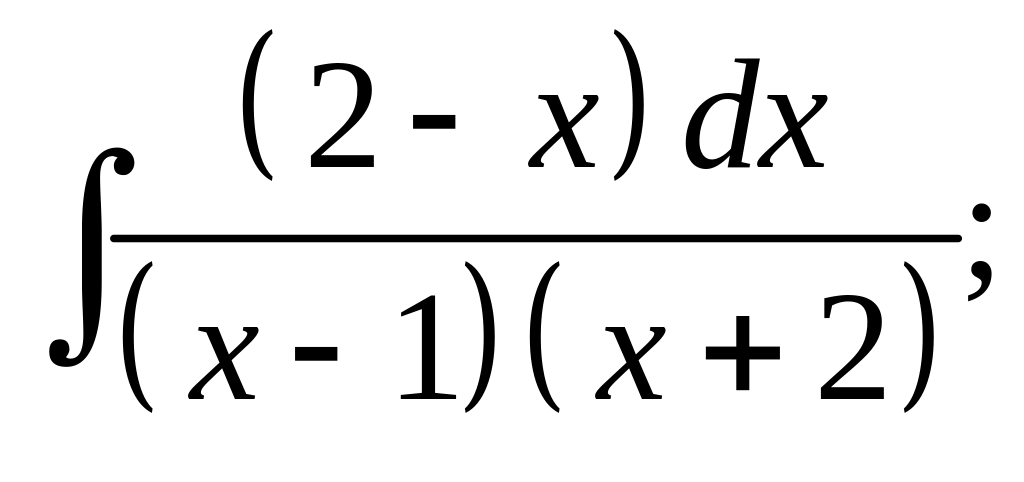 б)
б)
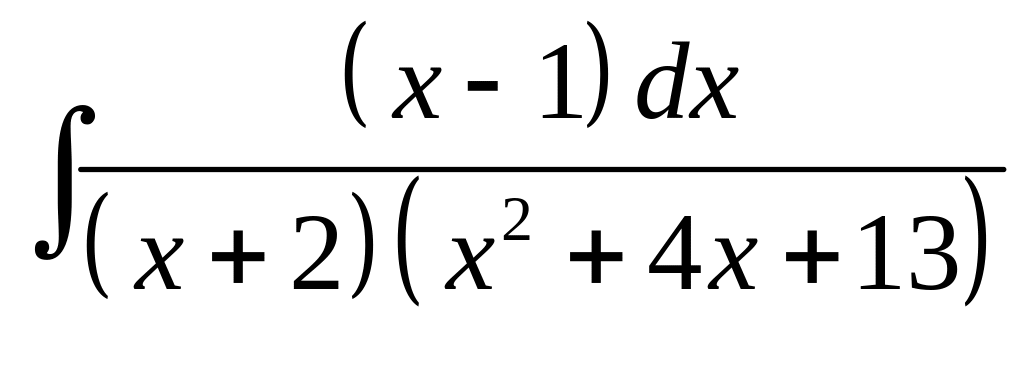 .
.
4. а)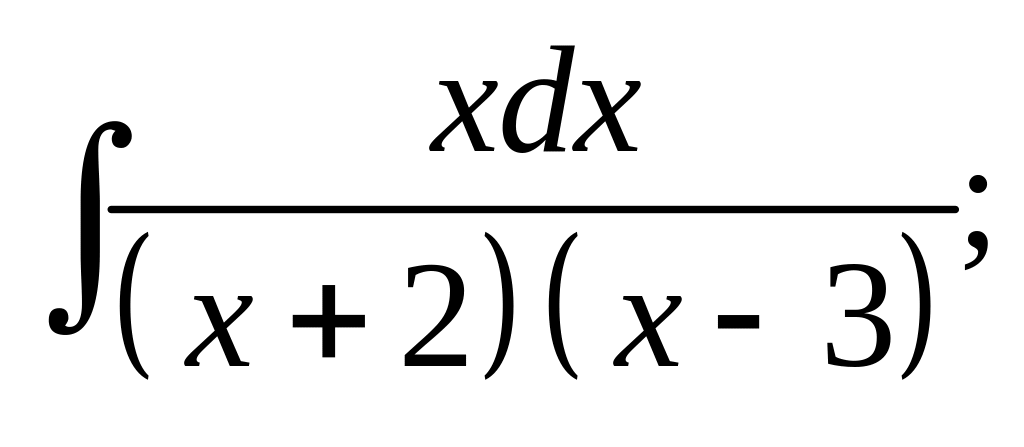 б)
б)
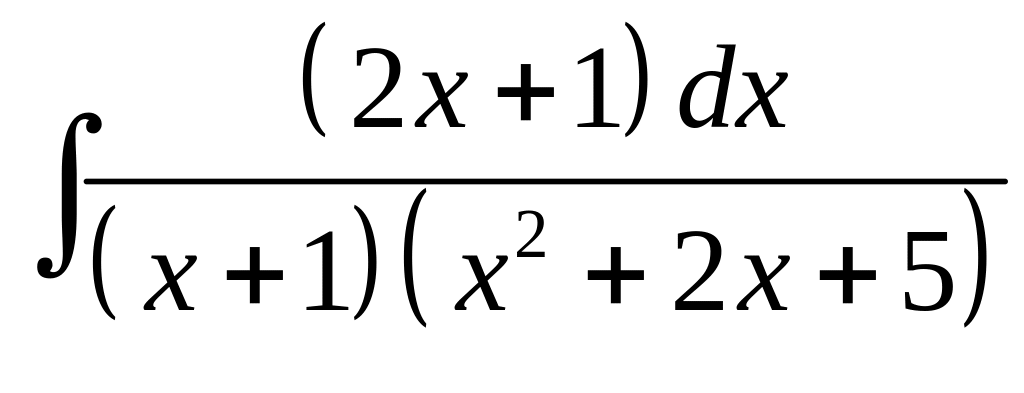 .
.
5. а)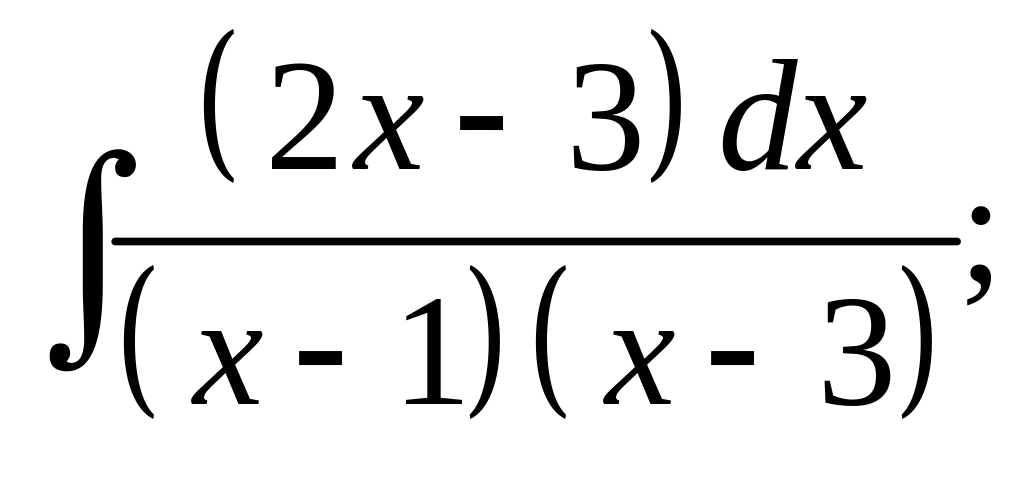 б)
б)
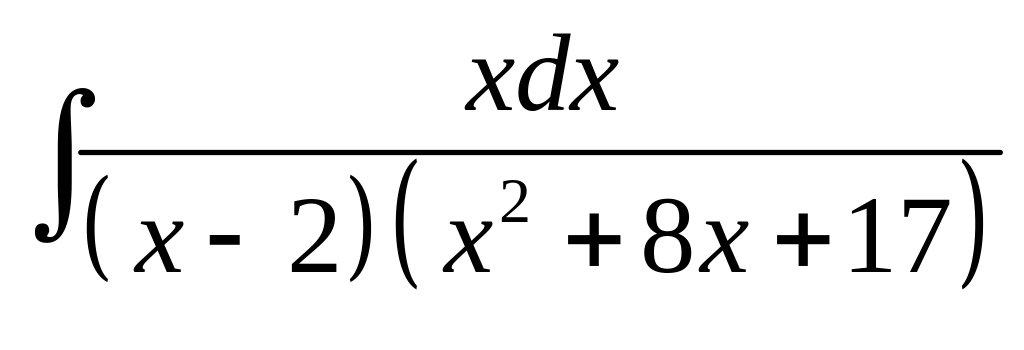 .
.
6. а)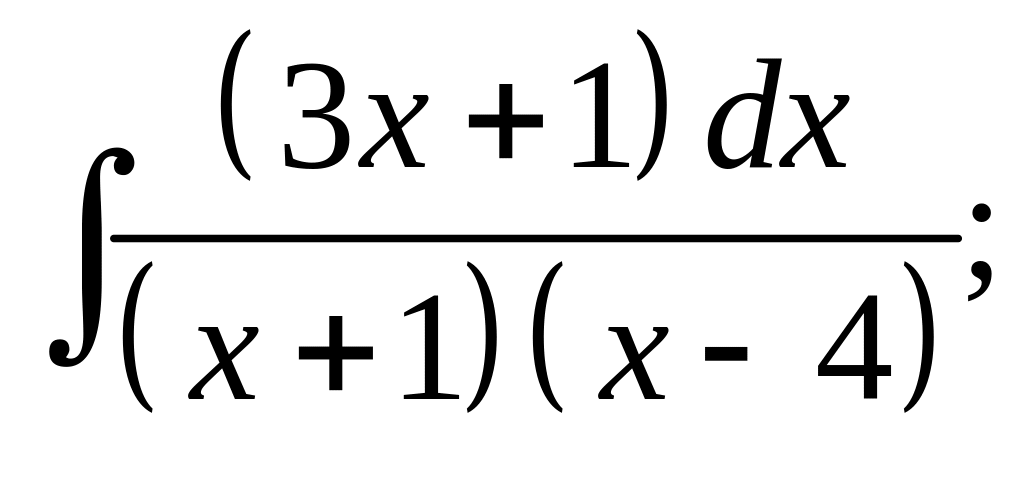 б)
б)
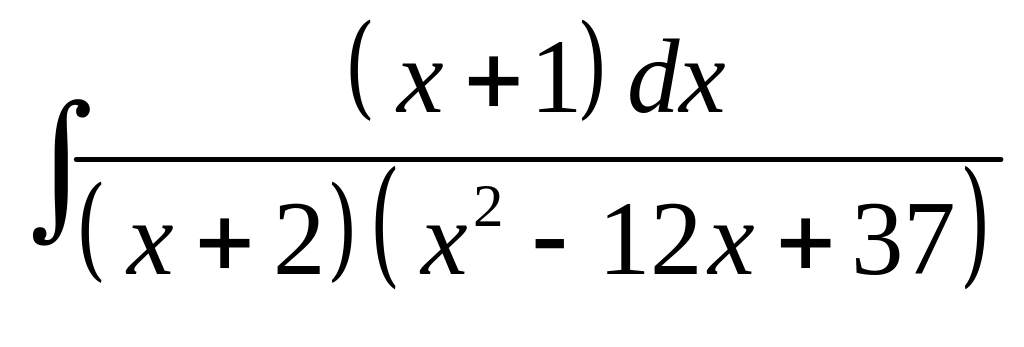 .
.
7. а)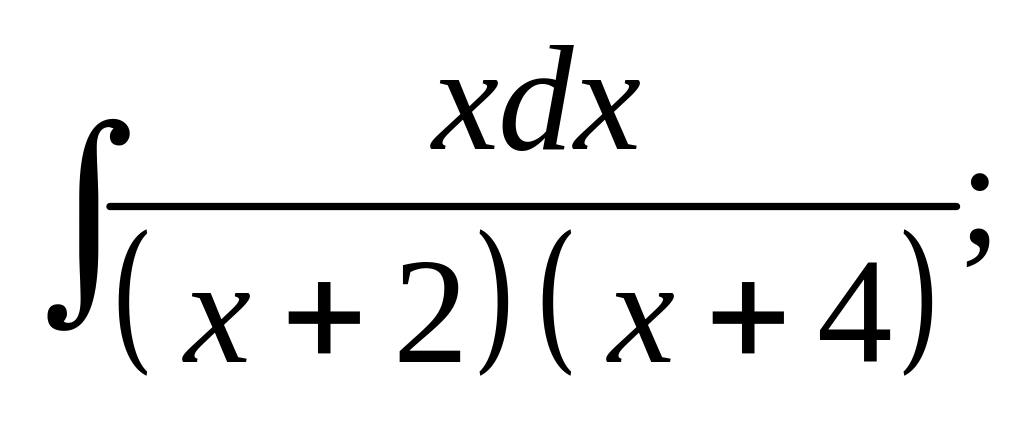 б)
б)
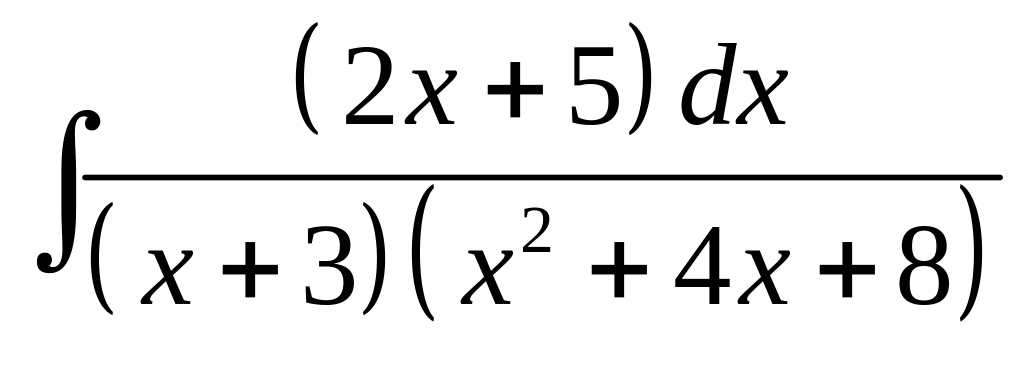 .
.
8. а)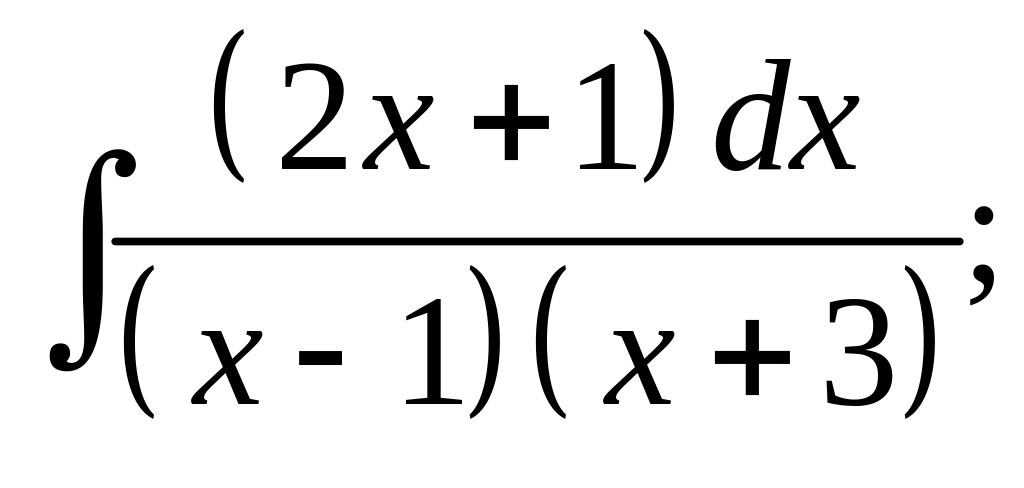 б)
б)
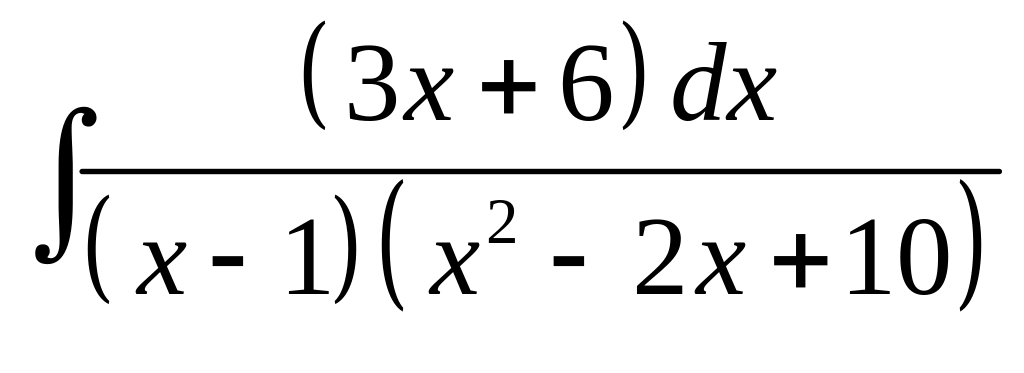 .
.
9. а)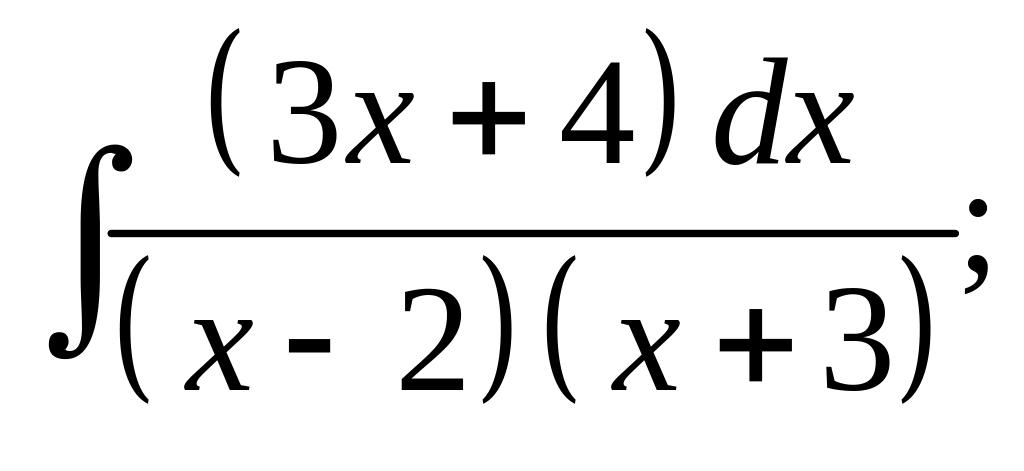 б)
б)
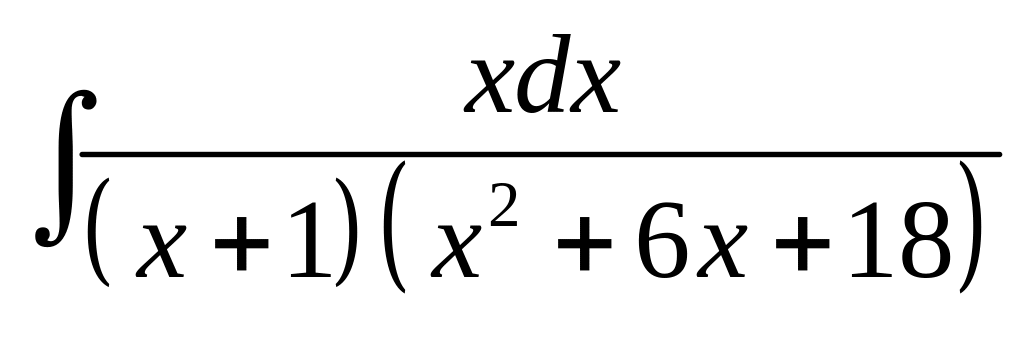 .
.
10. а)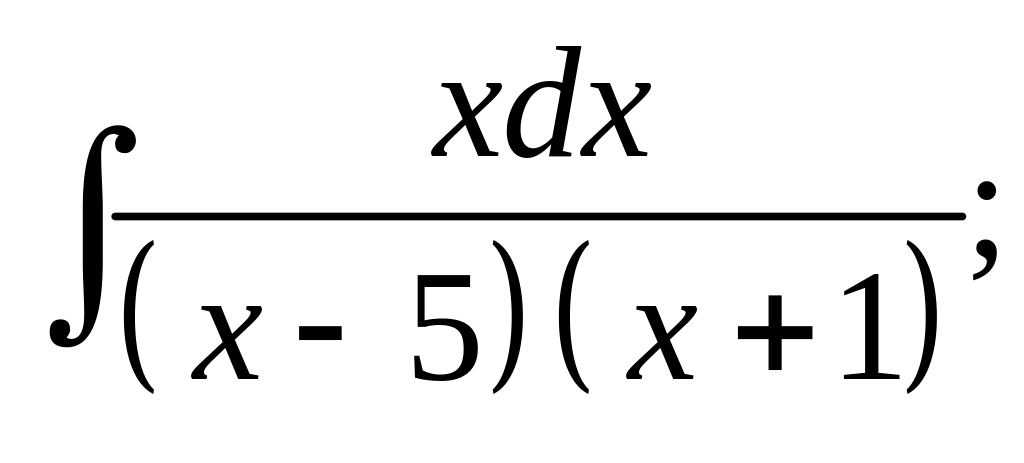 б)
б)
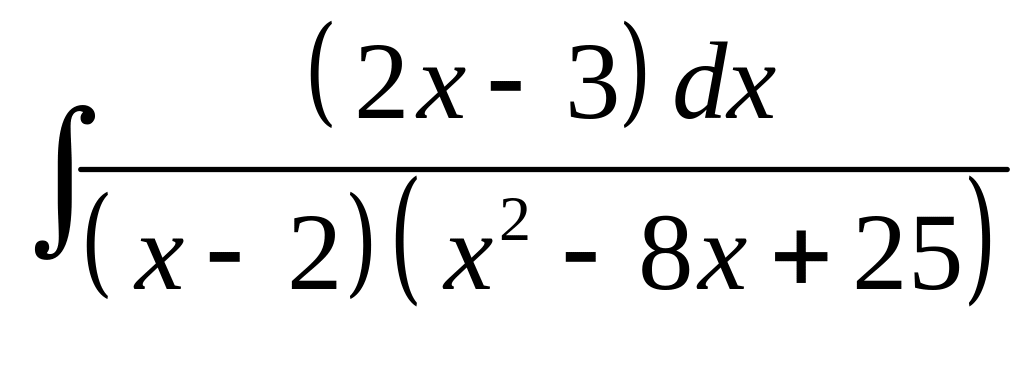 .
.
11. а)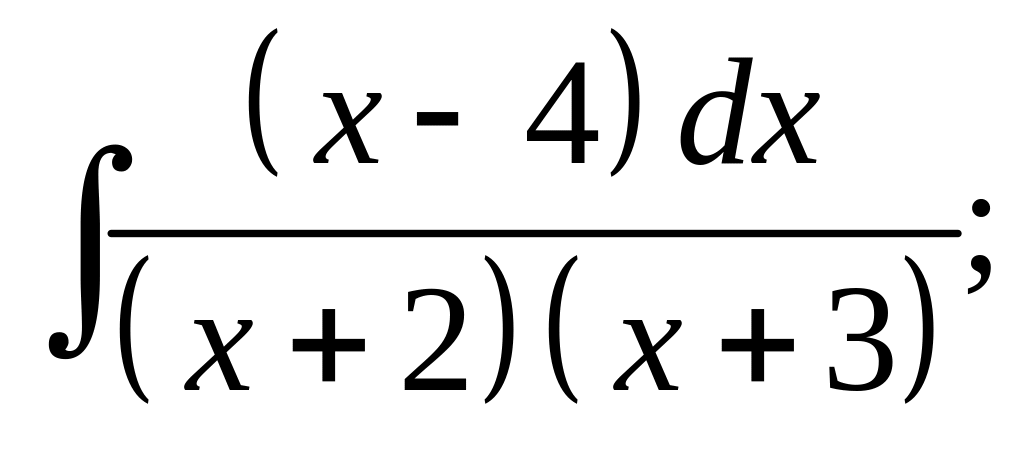 б)
б)
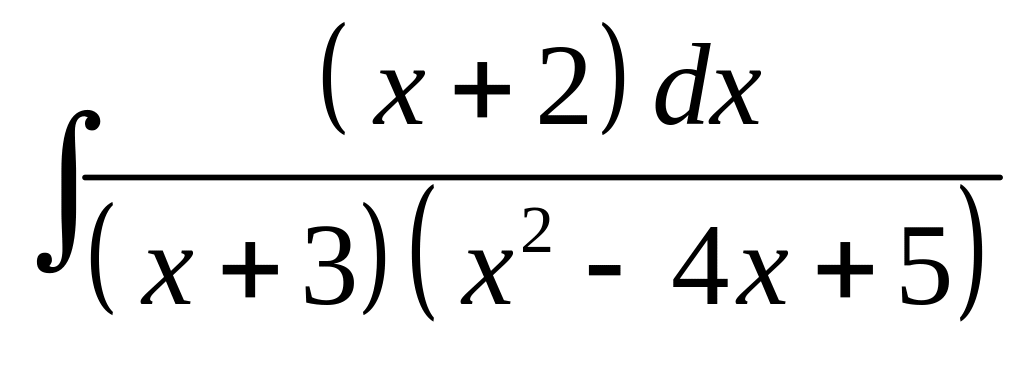 .
.
12. а)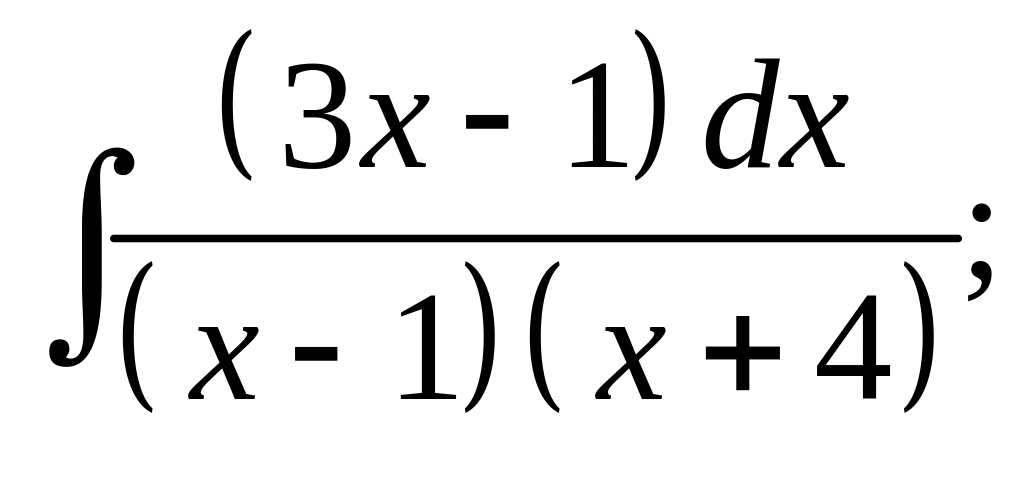 б)
б)
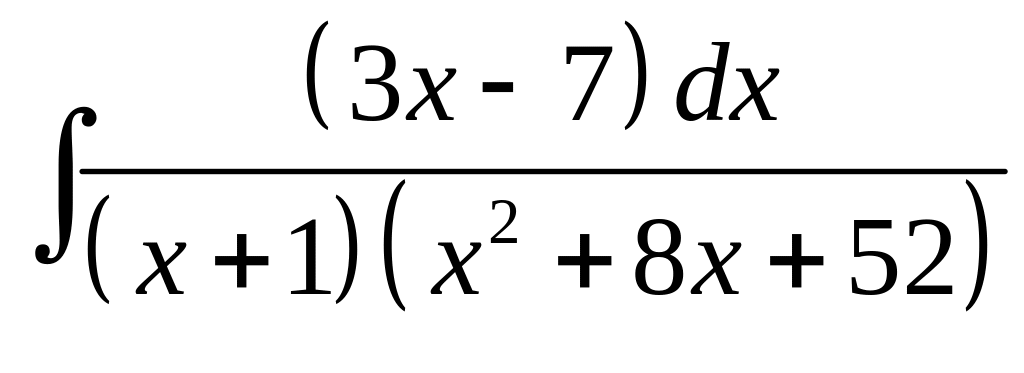 .
.
13. а)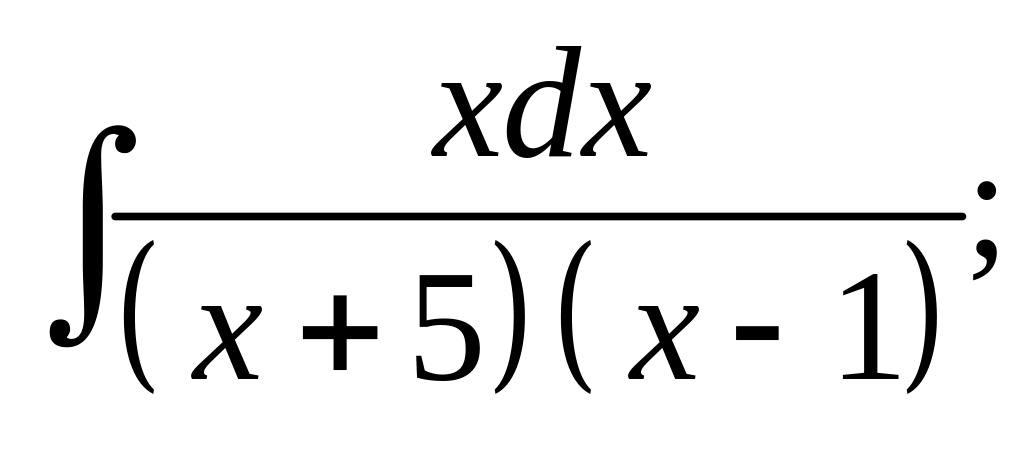 б)
б)
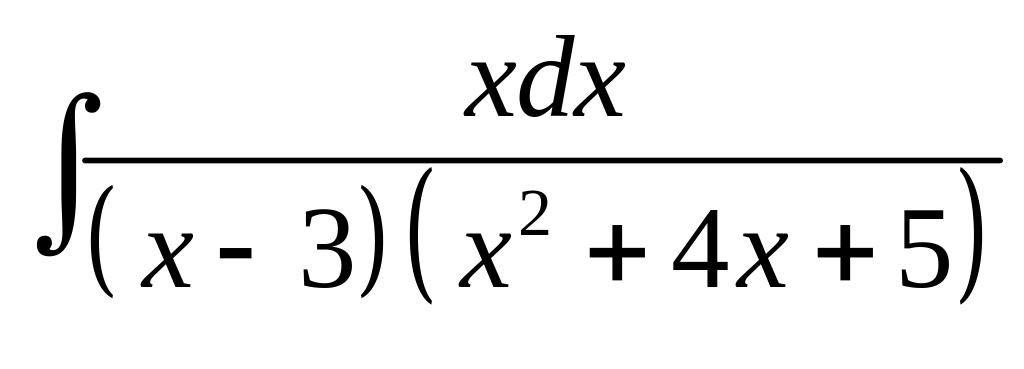 .
.
14. а)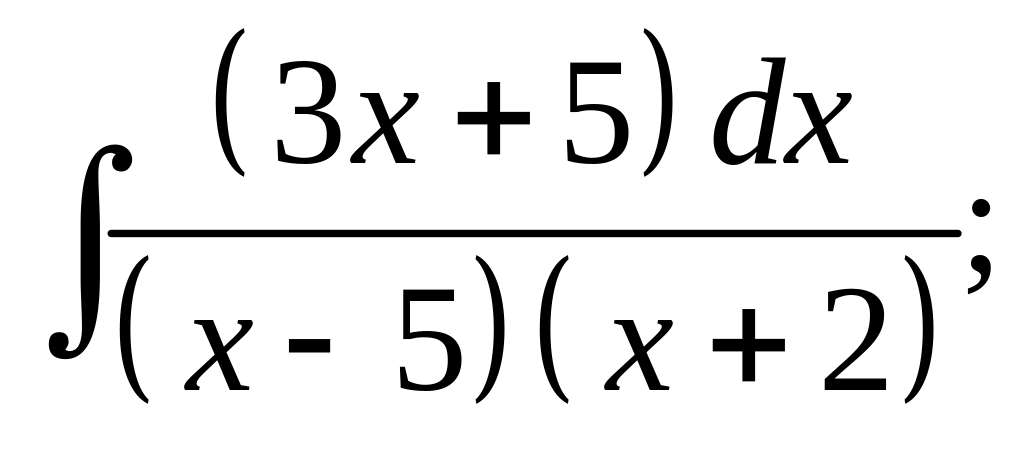 б)
б)
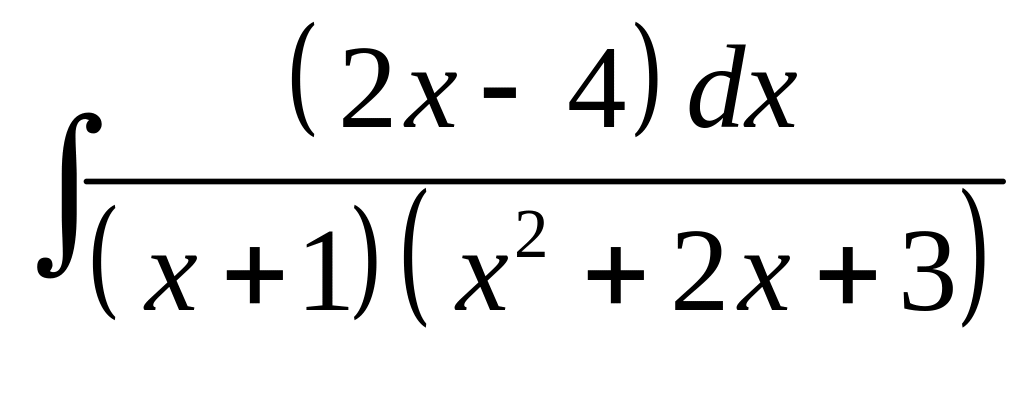 .
.
15. а)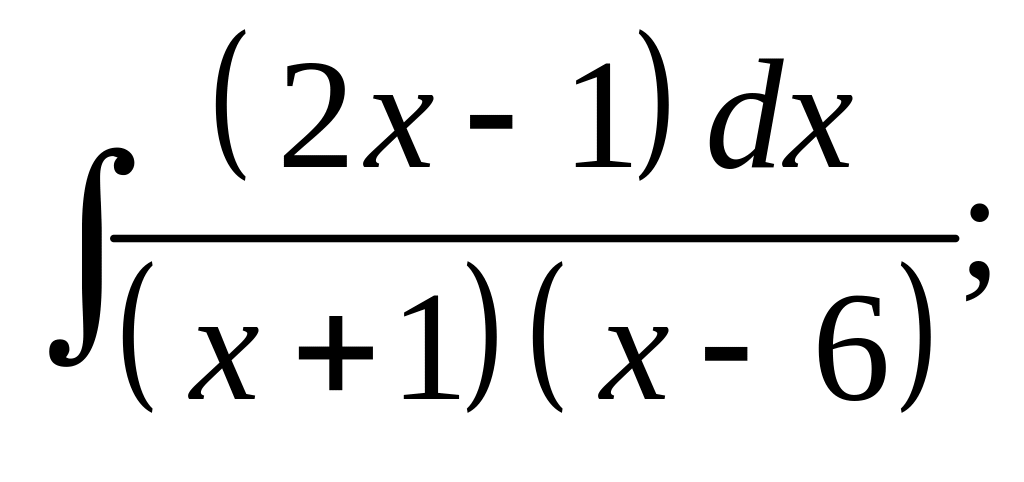 б)
б)
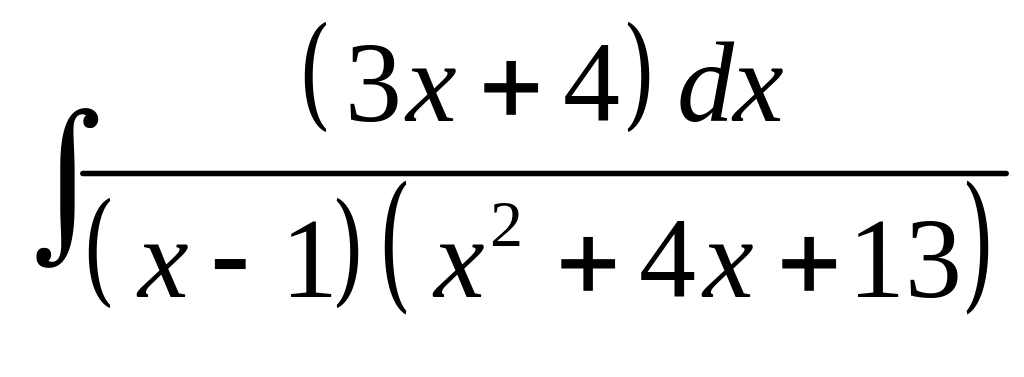 .
.
16. а)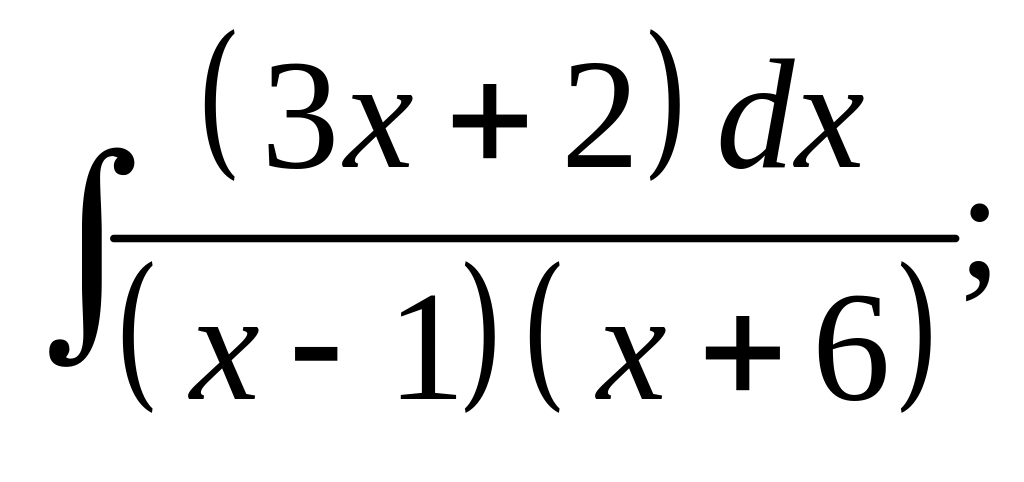 б)
б)
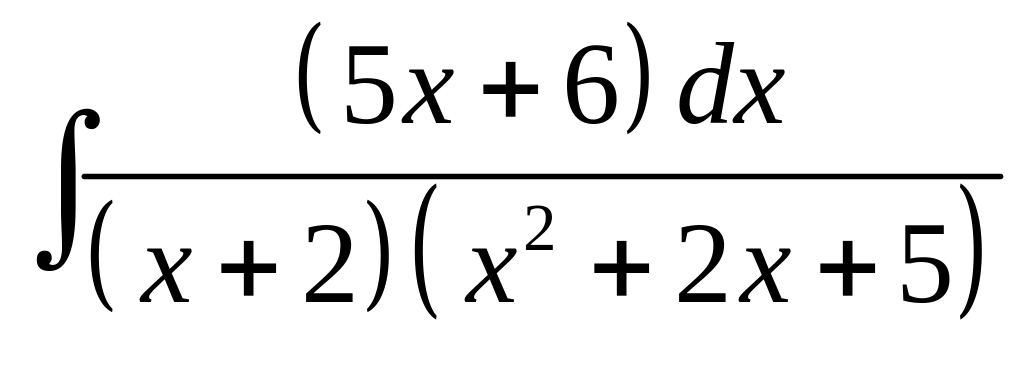 .
.
17. а)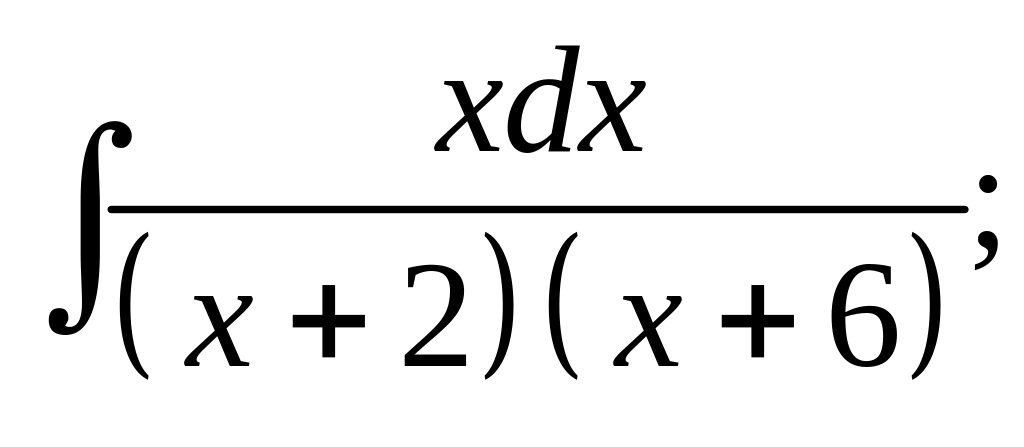 б)
б)
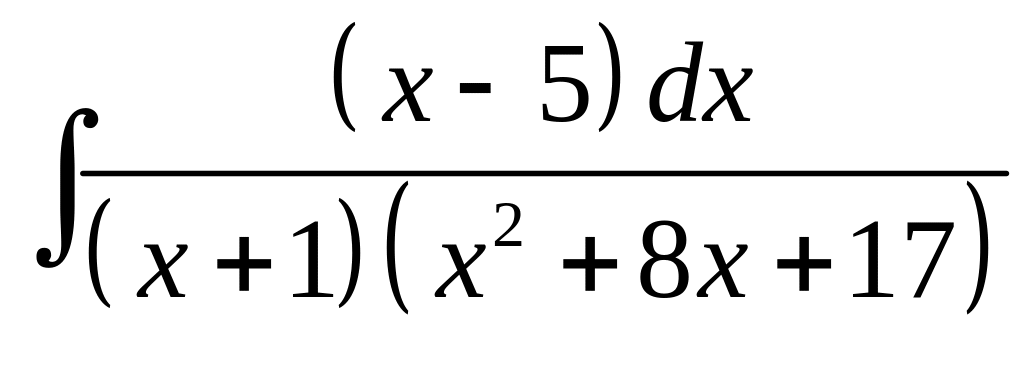 .
.
18. а)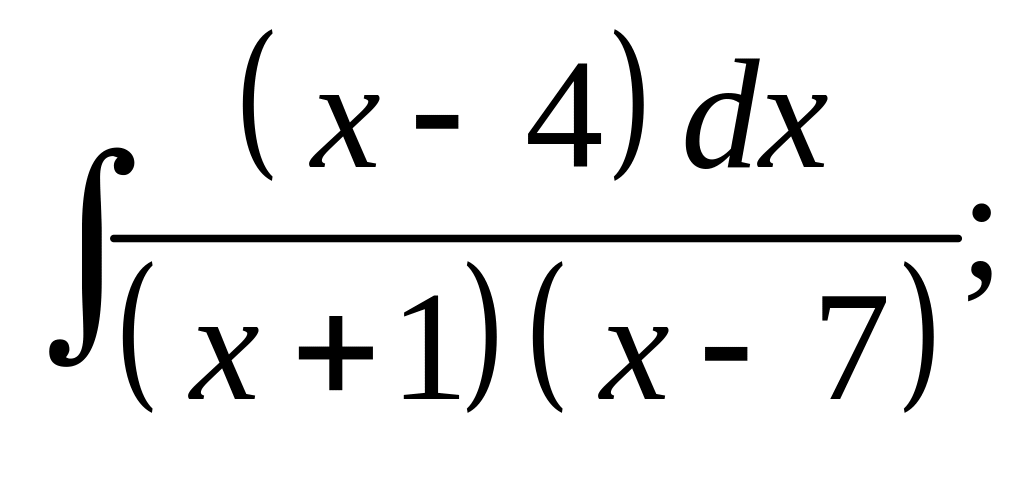 б)
б)
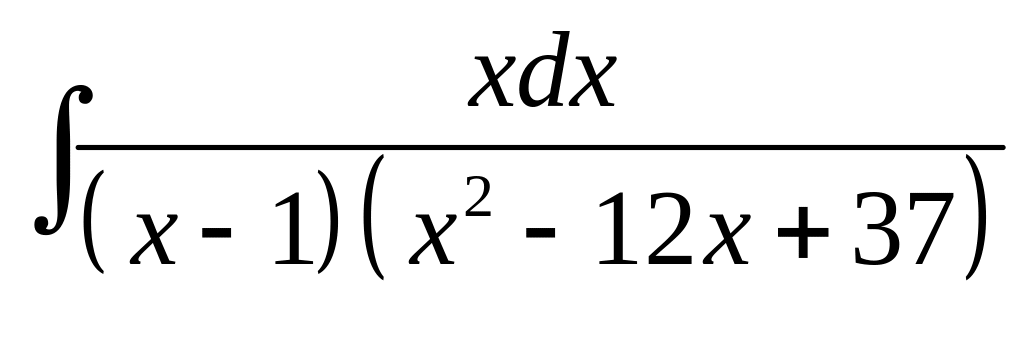 .
.
19. а)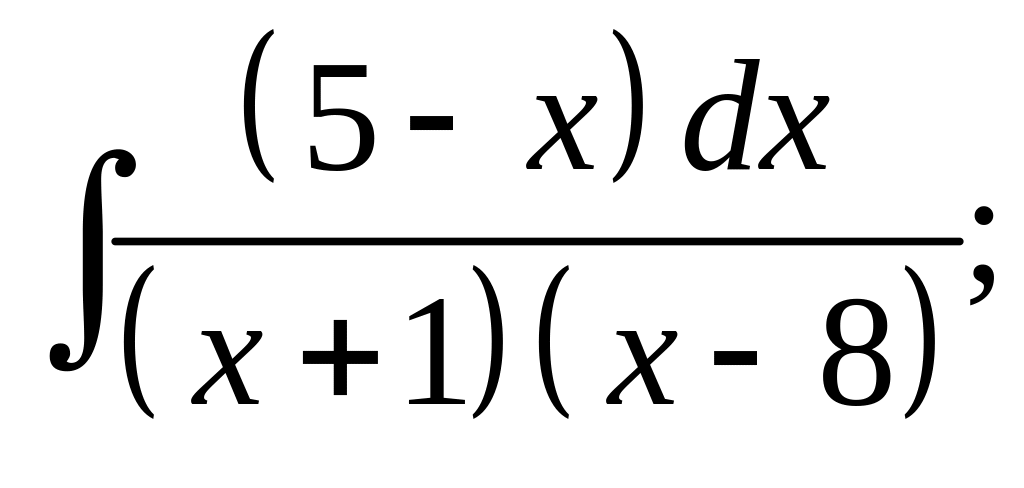 б)
б)
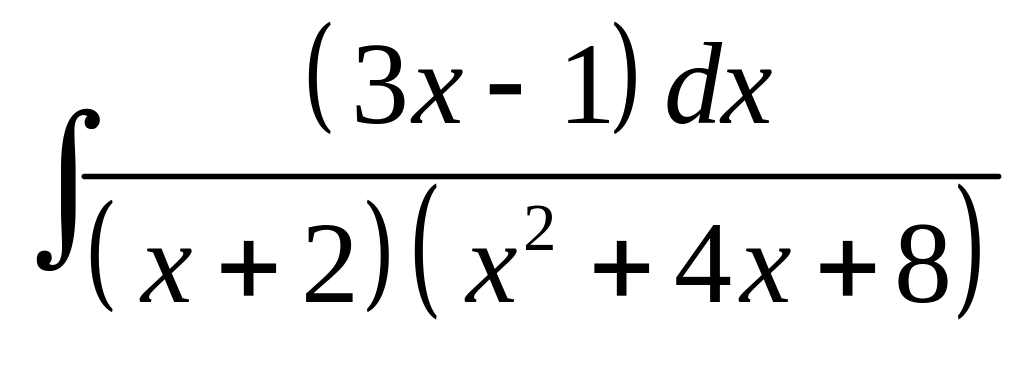 .
.
20. а)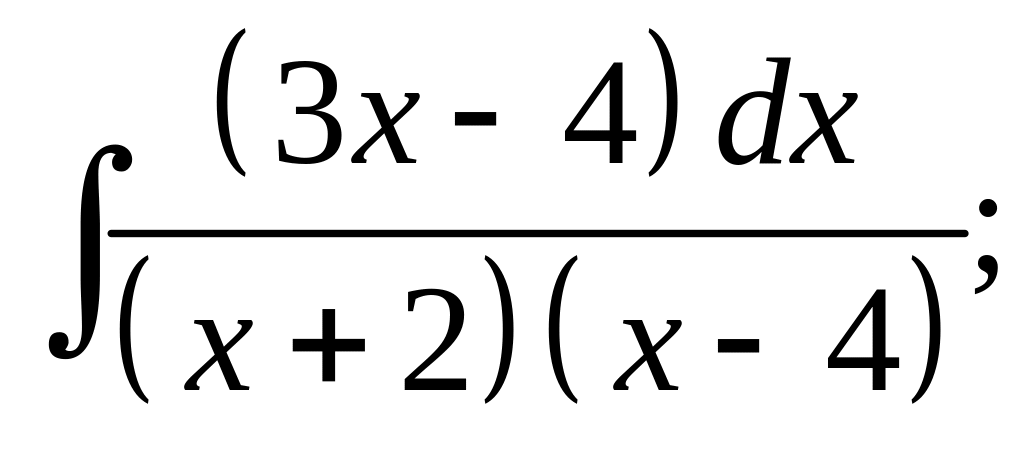 б)
б)
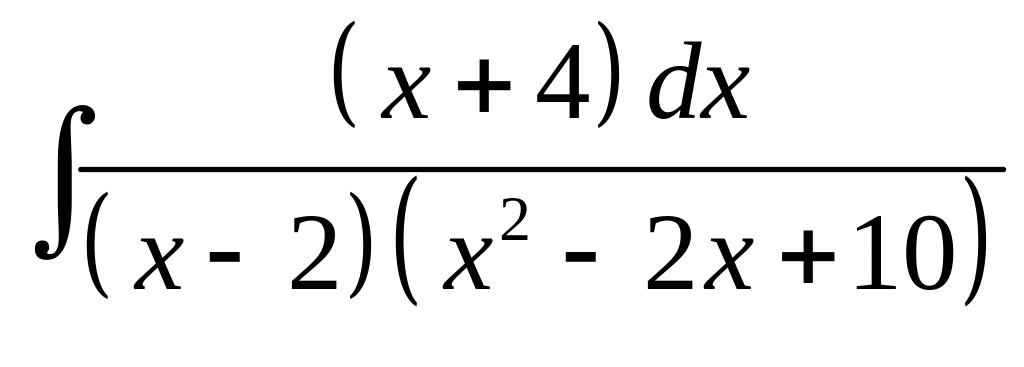 .
.
21. а)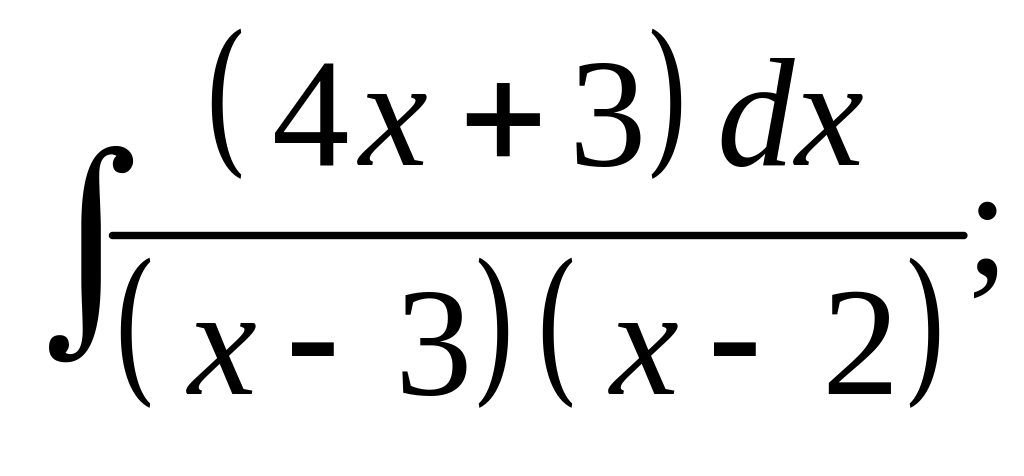 б)
б)
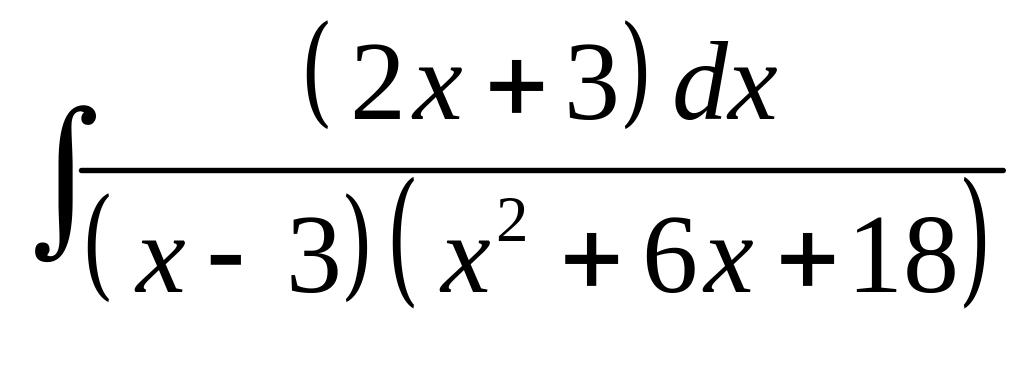 .
.
22. а)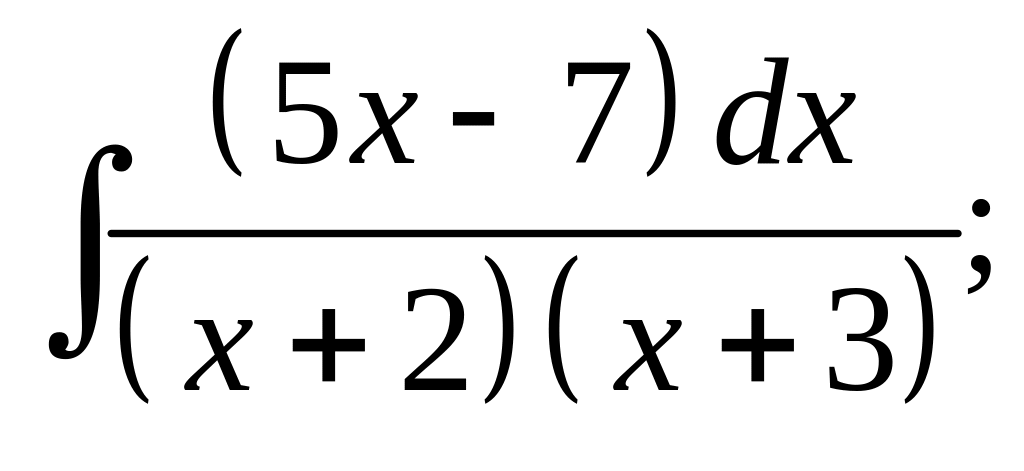 б)
б)
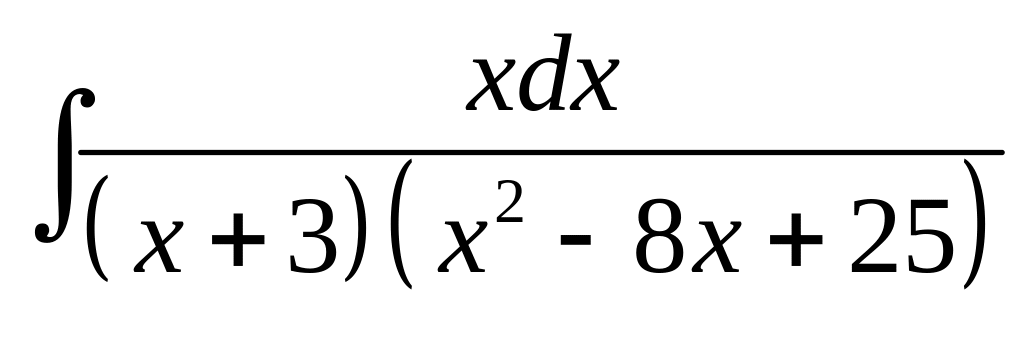 .
.
23. а)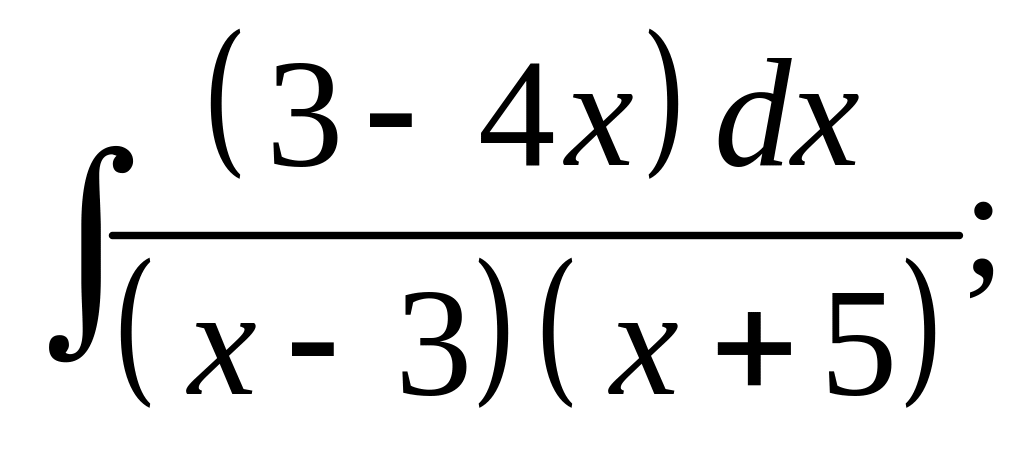 б)
б)
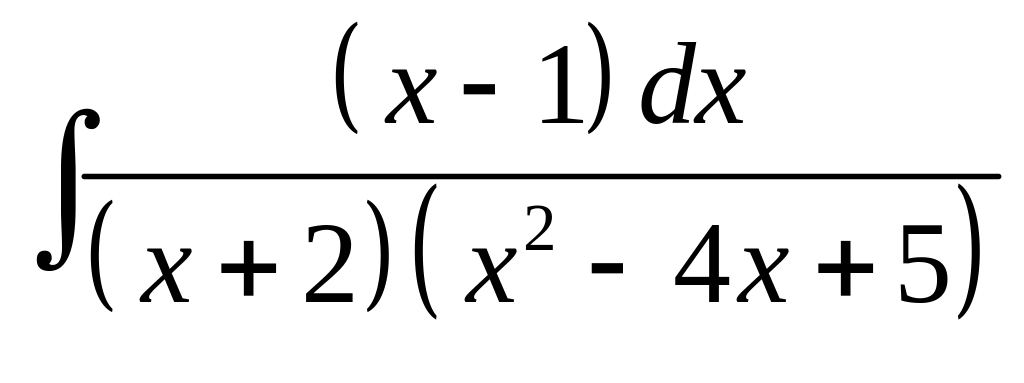 .
.
24. а)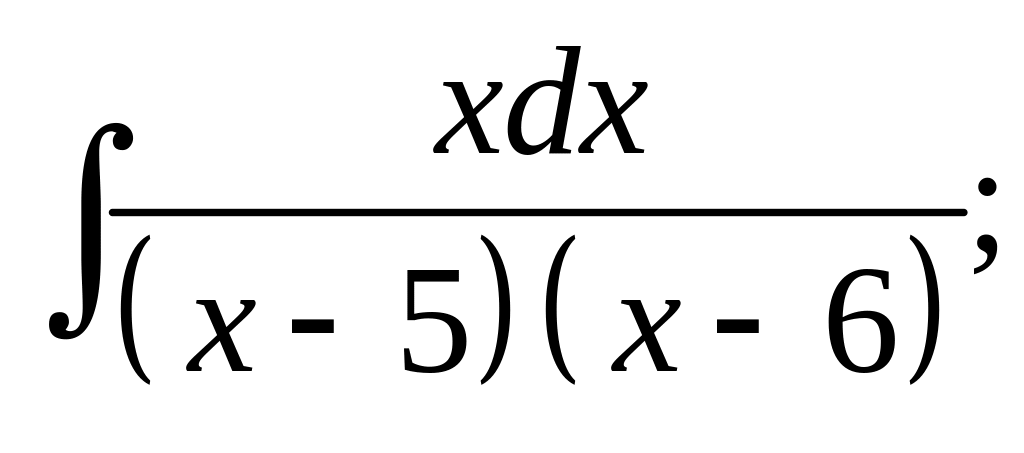 б)
б)
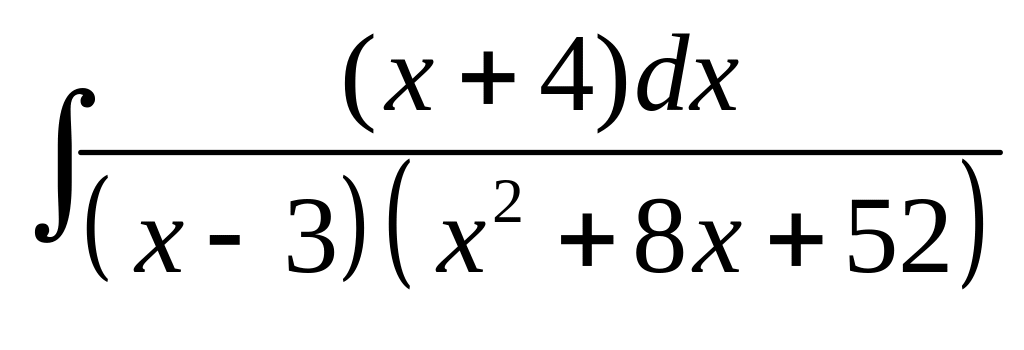 .
.
25. а)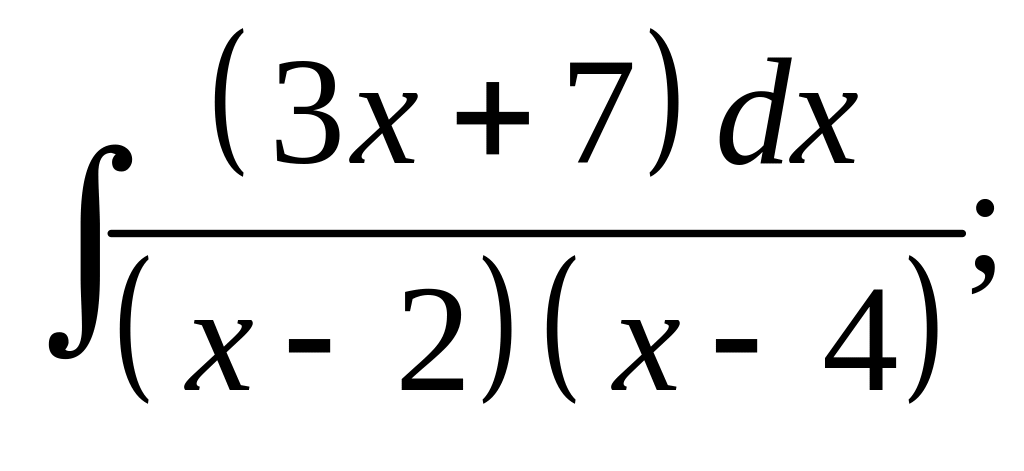 б)
б)
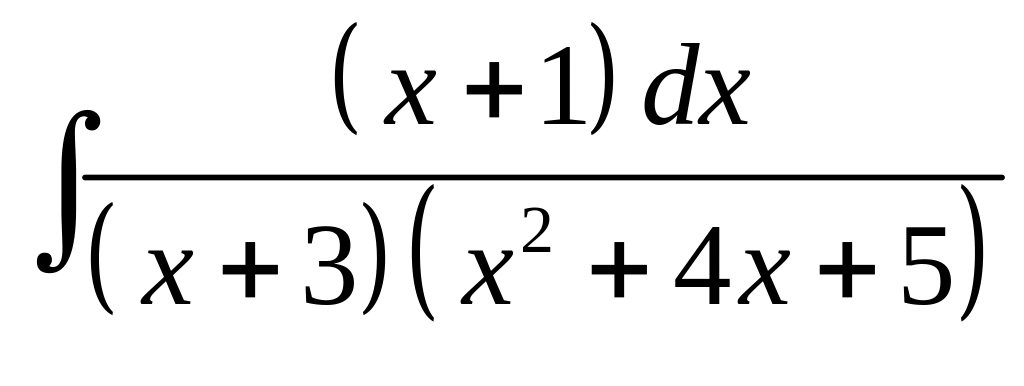 .
.
26. а)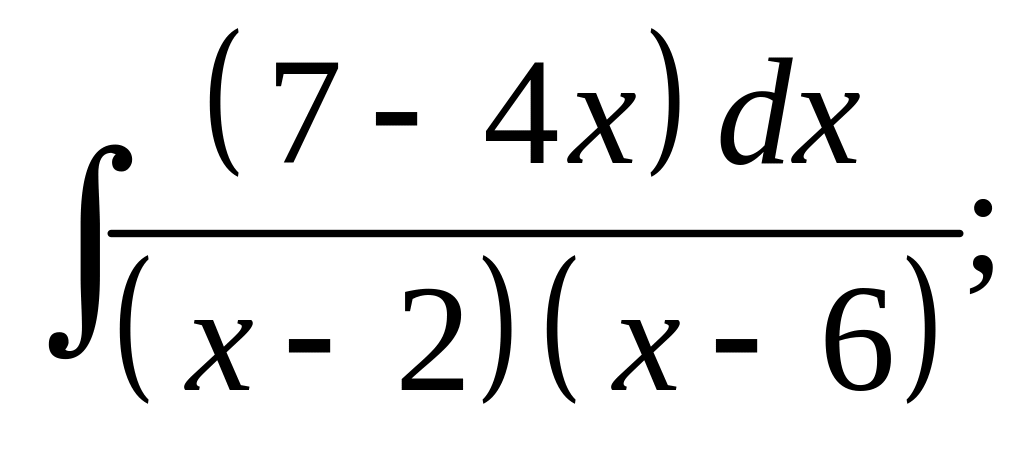 б)
.
б)
.
27. а)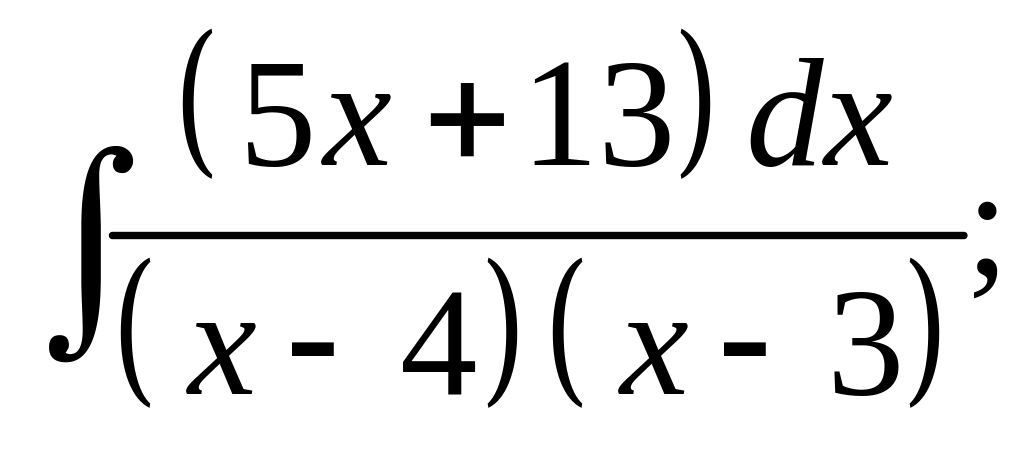 б)
б)
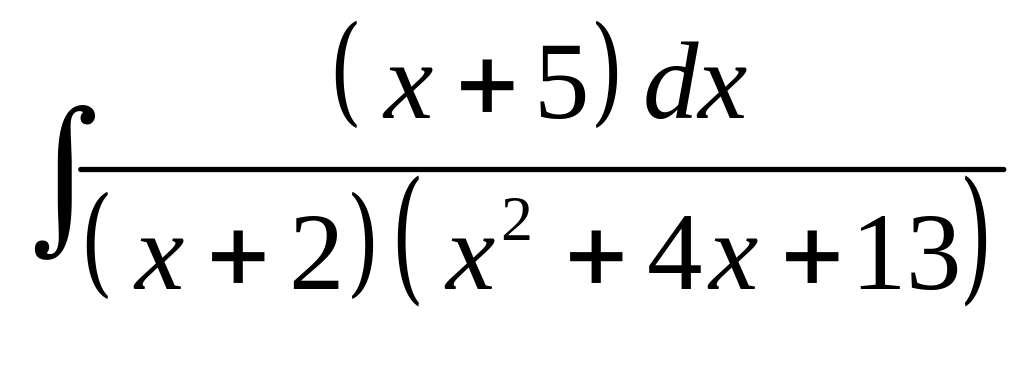 .
.
28. а)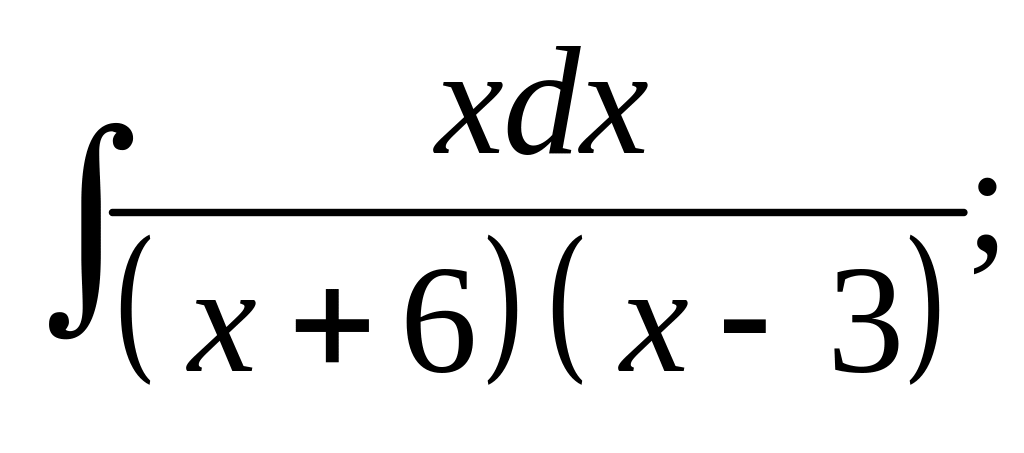 б)
б)
 .
.
29. а)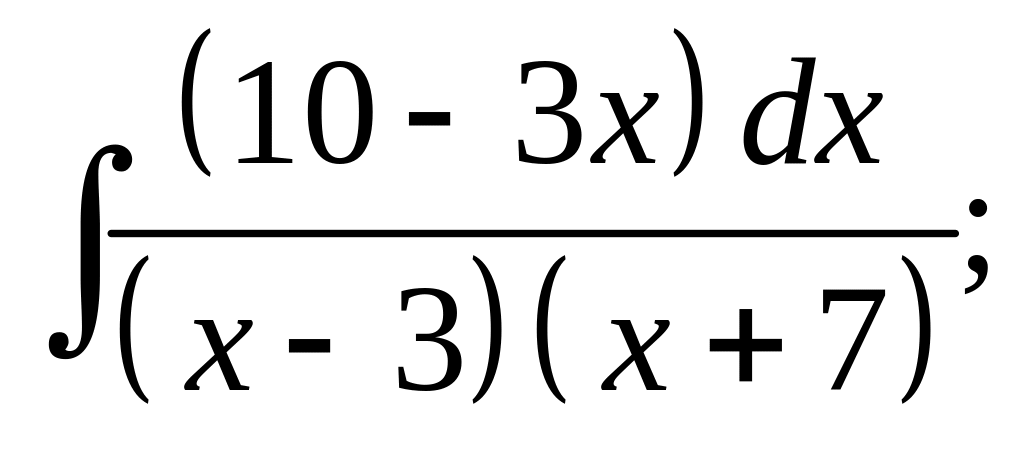 б)
б)
 .
.
30. а)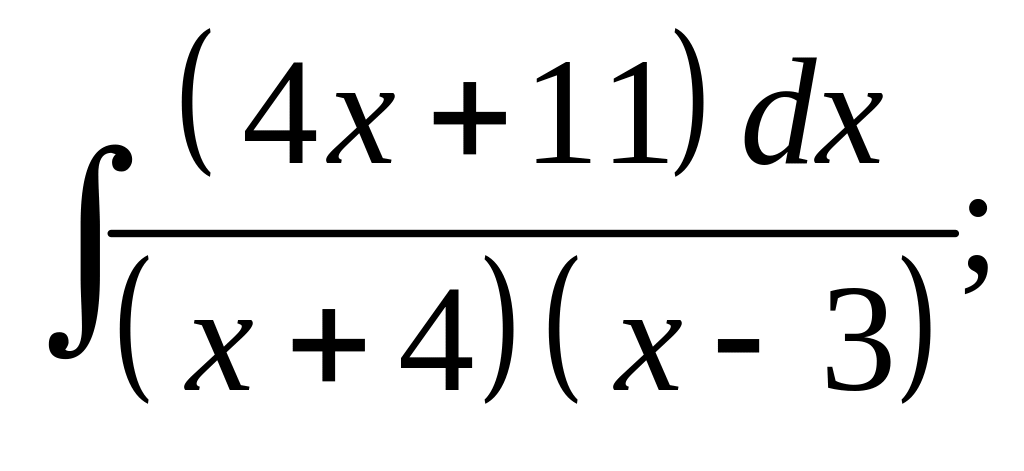 б)
б)
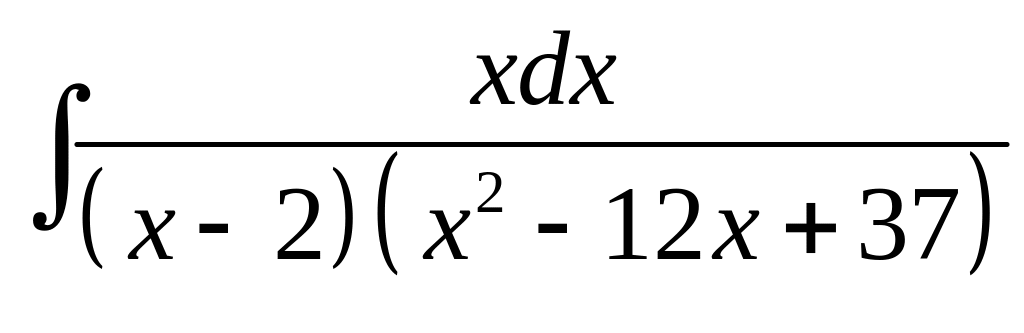 .
.
VIII. Найти неопределенные интегралы от выражений, содержащих тригонометрические функции.
1. а)
![]() ;
б)
;
б)
![]() .
.
2. а)
; б)
![]() .
.
3. а)
![]() ; б)
; б)
![]() .
.
4. а)
![]() ;
б)
;
б)
![]() .
.
5. а)
![]() ;
б)
;
б)
![]() .
.
6. а)
![]() ;
б)
;
б)
![]() .
.
7. а)
![]() ;
б)
;
б)
![]() .
.
8. а)
![]() ;
б)
;
б)
![]() .
.
9. а)
![]() ;
б)
;
б)
![]() .
.
10. а)
![]() ;
б)
;
б)
![]() .
.
11. а)
![]() ;
б)
;
б)
![]() .
.
12. а)
![]() ;
б)
;
б)
![]() .
.
13. а)
![]() ;
б)
;
б)
![]() .
.
14. а)
![]() ;
б)
;
б)
![]() .
.
15. а)
![]() ;
б)
;
б)
![]() .
.
16. а)
![]() ;
б)
;
б)
![]() .
.
17. а)
![]() ;
б)
;
б)
![]() .
.
18. а)
![]() ;
б)
;
б)
![]() .
.
19. а)
![]() ;
б)
;
б)
![]() .
.
20. а)
![]() ;
б)
;
б)
![]() .
.
21. а)
![]() ;
б)
;
б)
![]() .
.
22. а)
![]() ;
б)
;
б)
![]() .
.
23. а)
![]() ;
б)
;
б)
![]() .
.
24. а)
![]() ;
б)
.
;
б)
.
25. а)
![]() ;
б)
;
б)
![]() .
.
26. а)
![]() ;
б)
;
б)
![]() .
.
27. а)
![]() ;
б)
;
б)
![]() .
.
28. а)
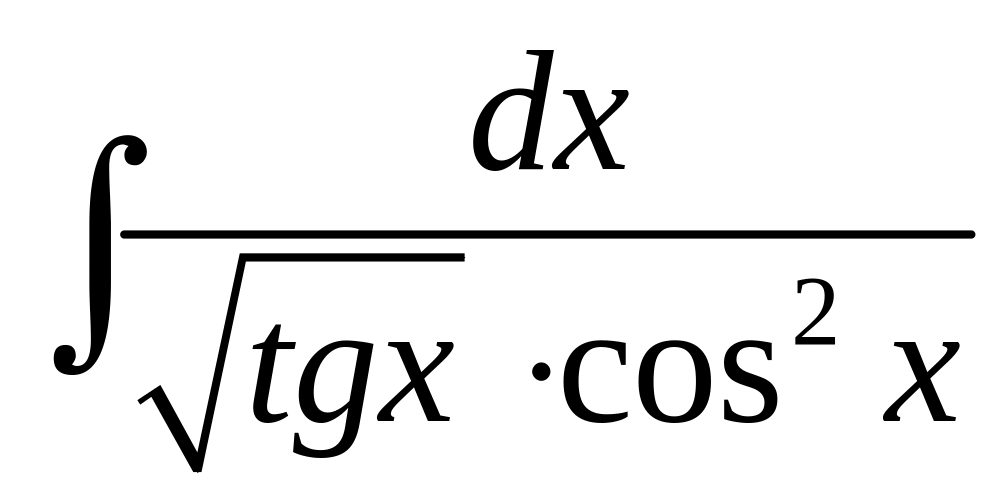 ;
б)
;
б)
![]() .
.
29. а)
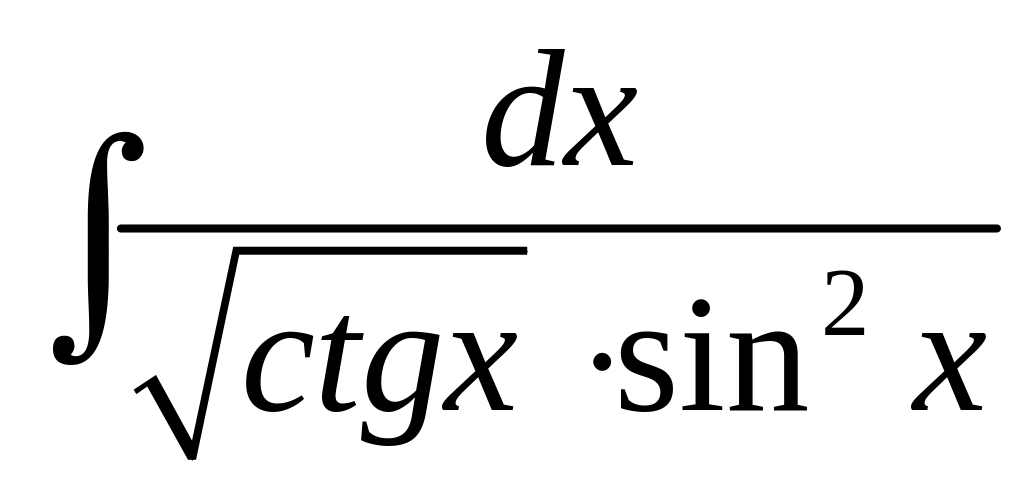 ;
б)
;
б)
![]() .
.
30. а)
![]() ;
б)
;
б)
![]() .
.
IX. Вычислить определенные интегралы.
а)
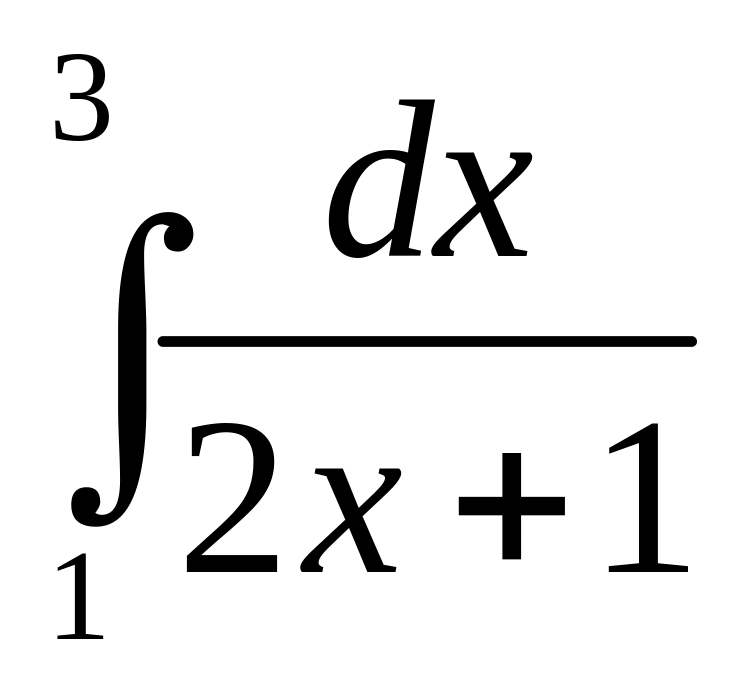 ;
б)
;
б)
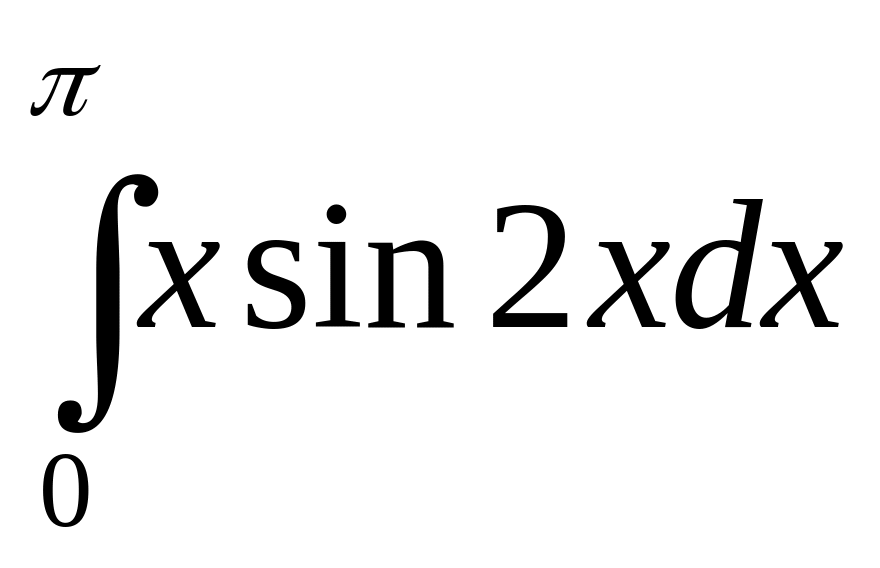 ;
в)
;
в)
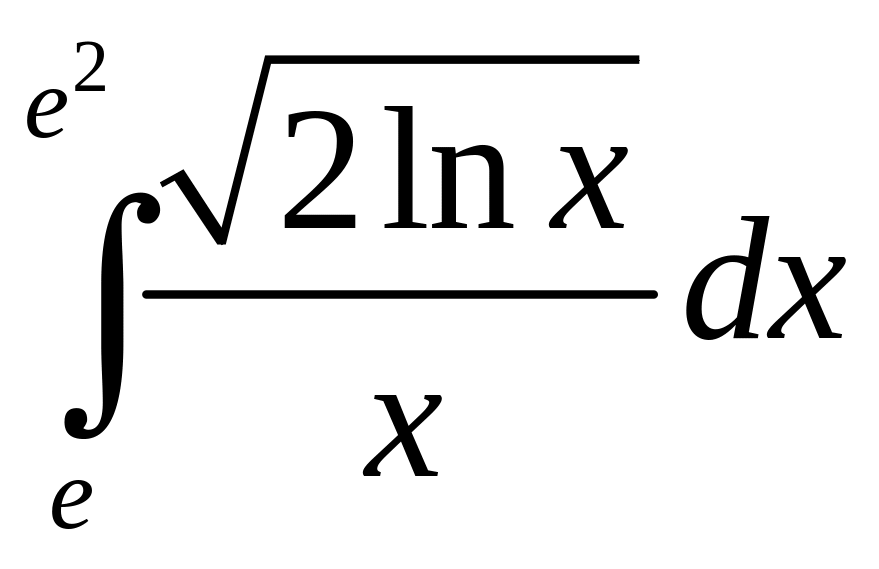 .
.а)
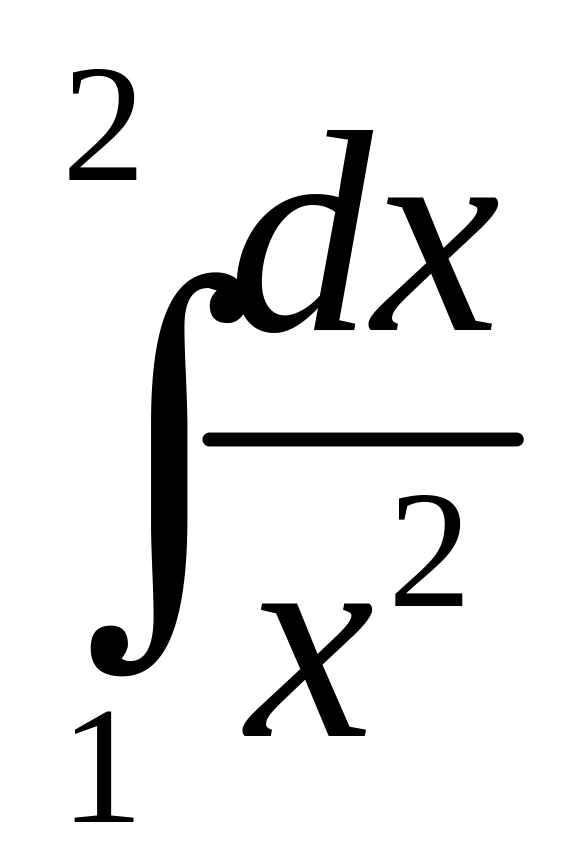 ;
б)
;
б)
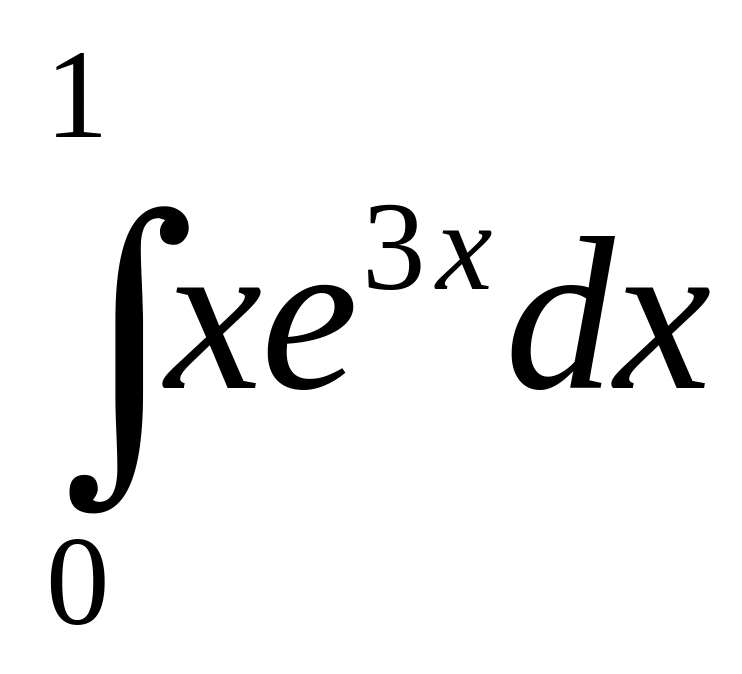 ;
в)
;
в)
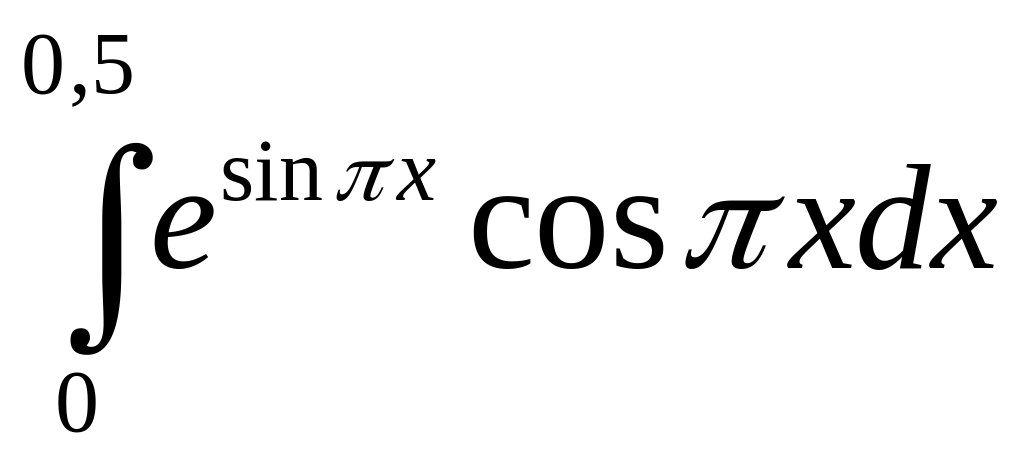 .
.а)
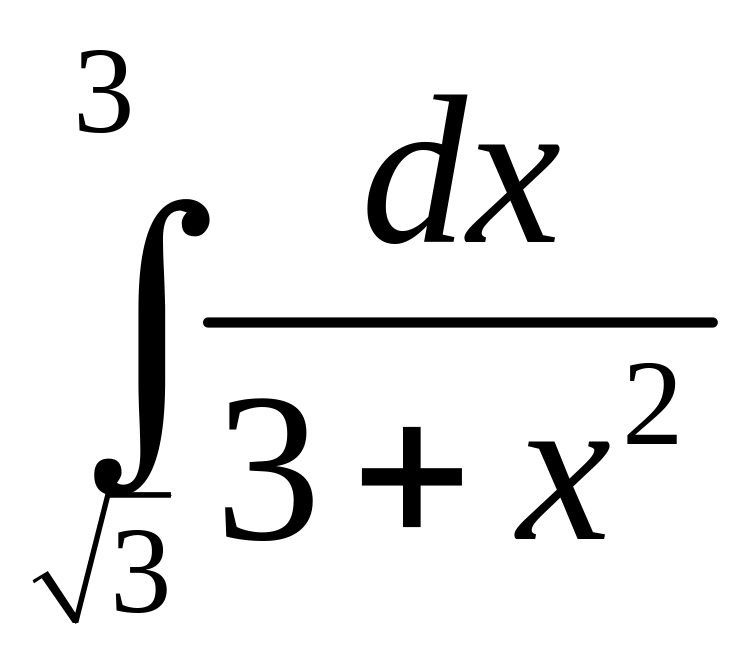 ;
б)
;
б)
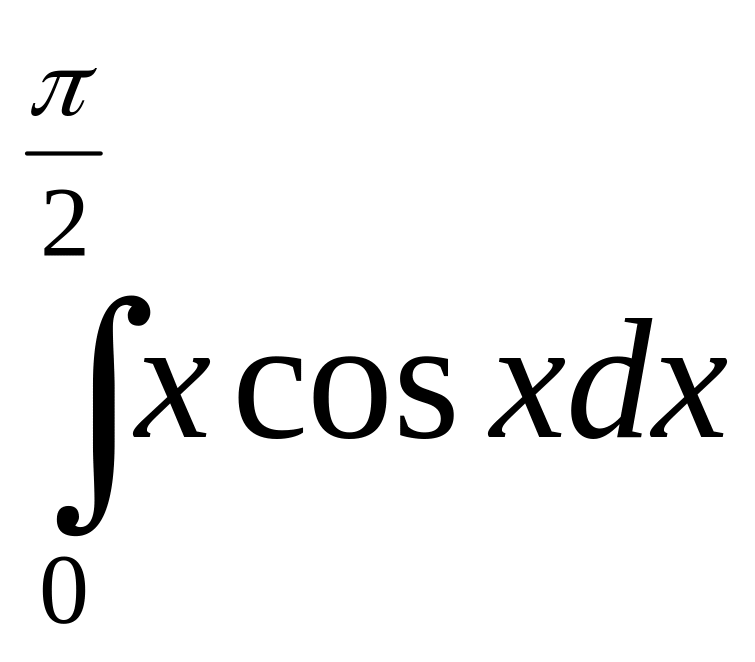 ;
в)
;
в)
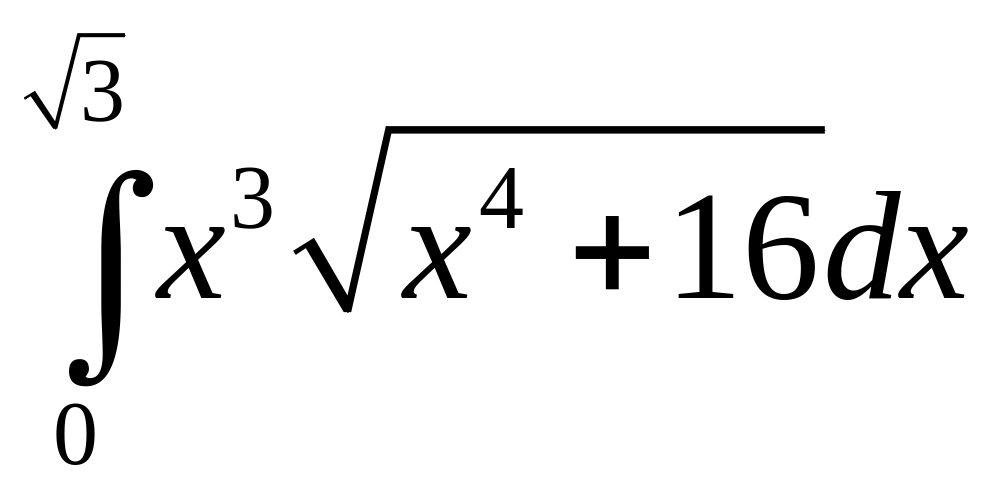 .
.а)
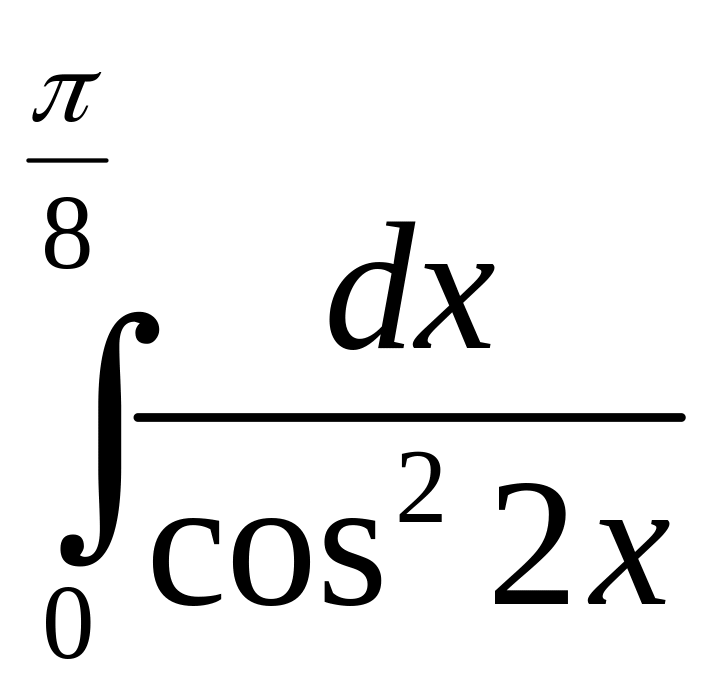 ;
б)
;
б)
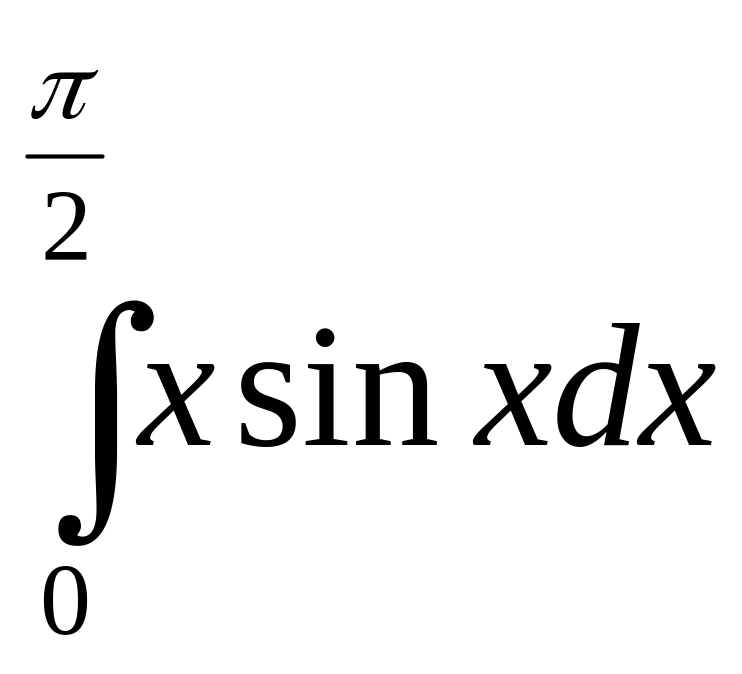 ;
в)
;
в)
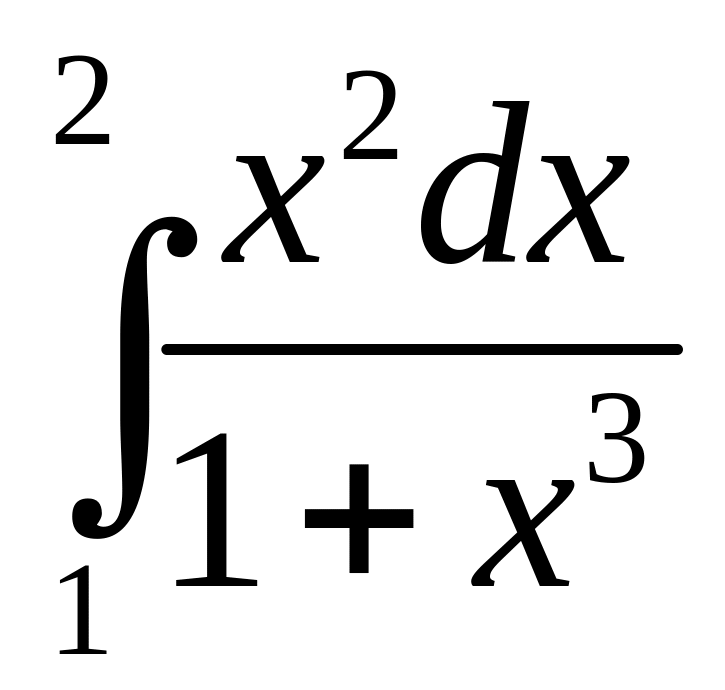 .
.а)
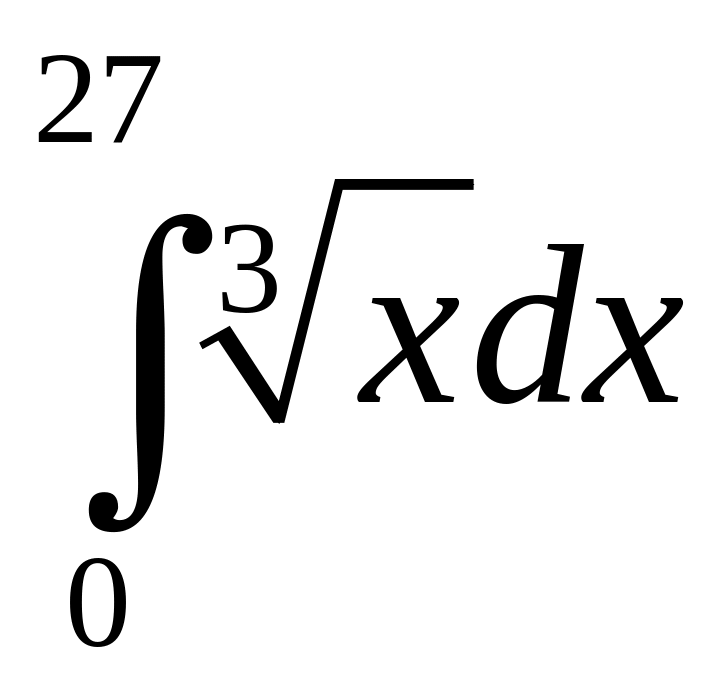 ;
б)
;
б)
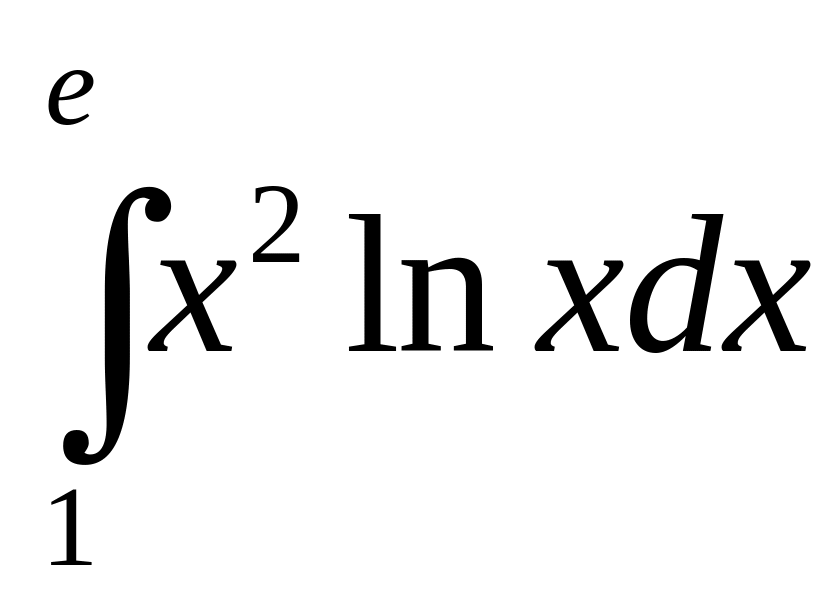 ;
в)
;
в)
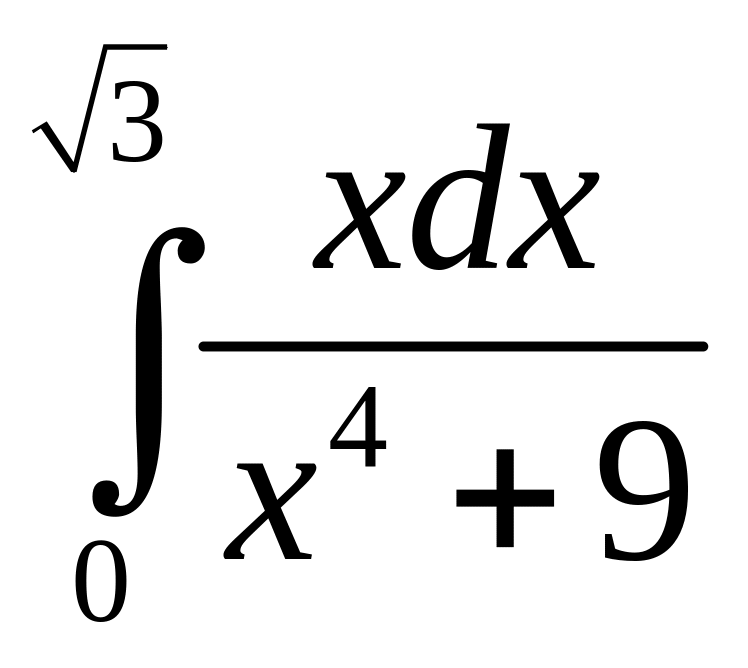 .
.а)
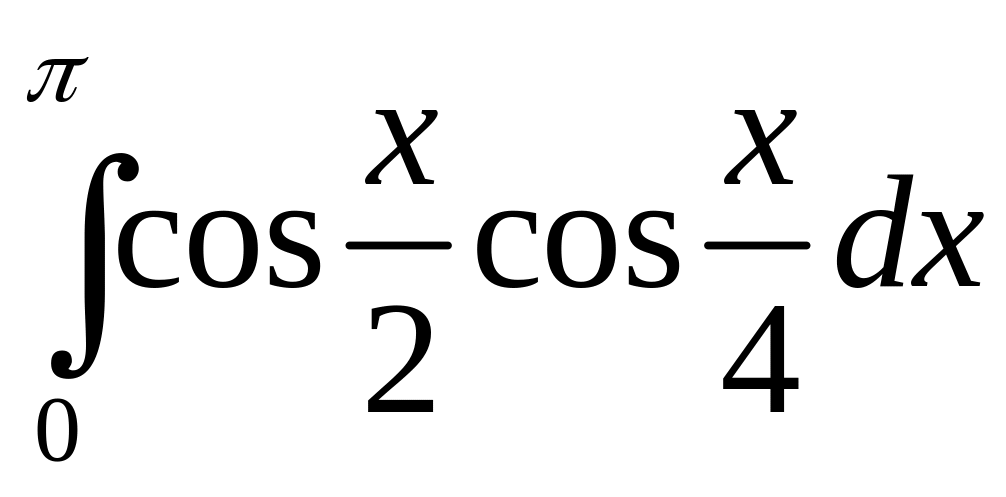 ;
б)
;
б)
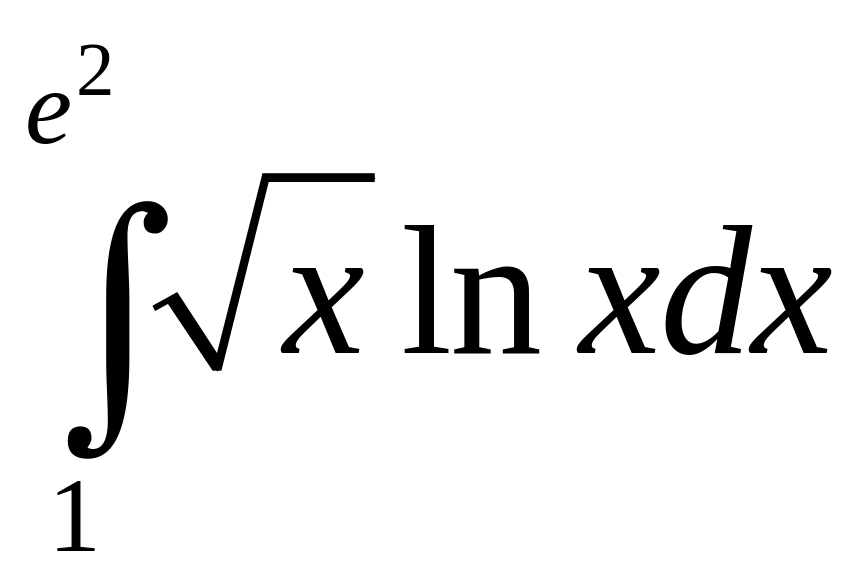 ;
в)
;
в)
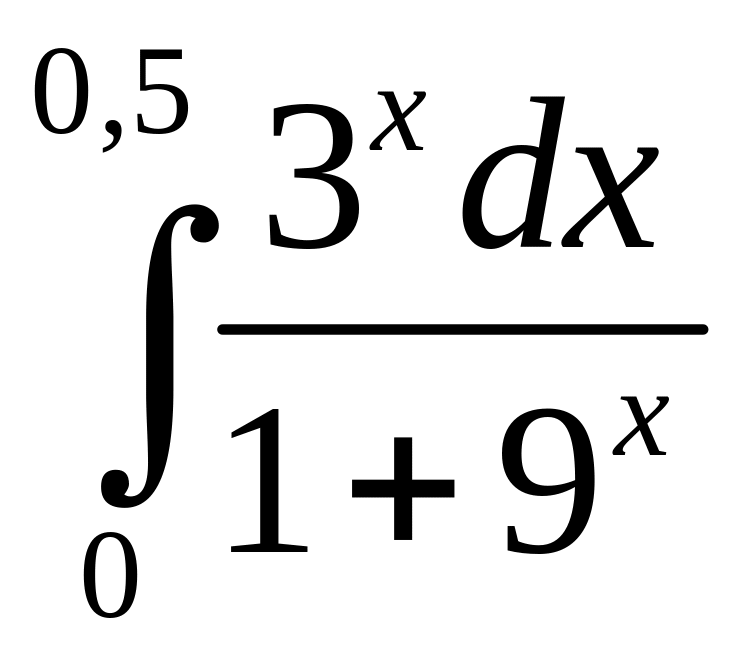 .
.а)
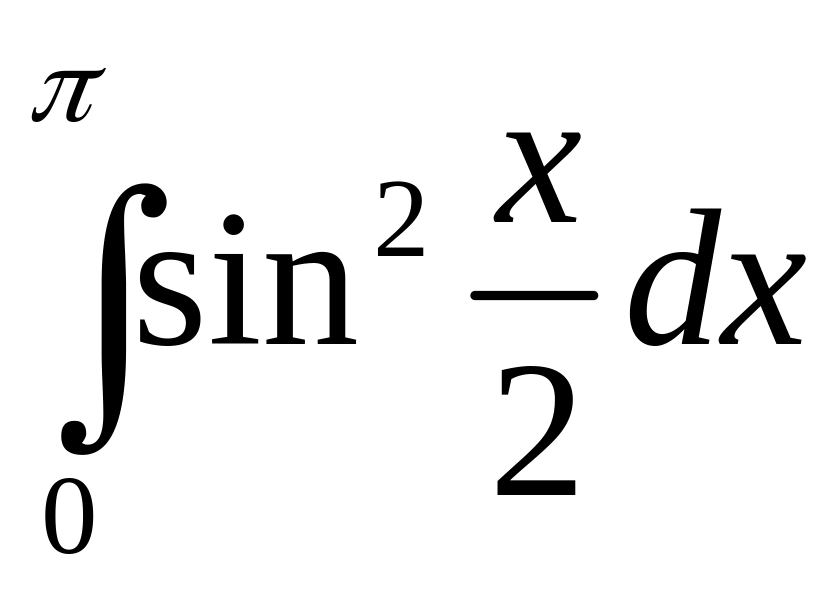 ;
б)
;
б)
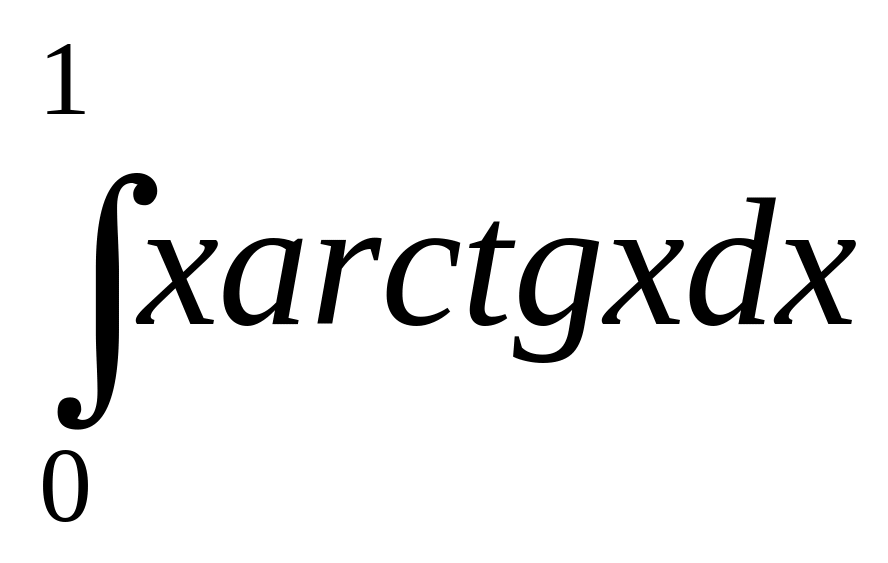 ;
в)
;
в)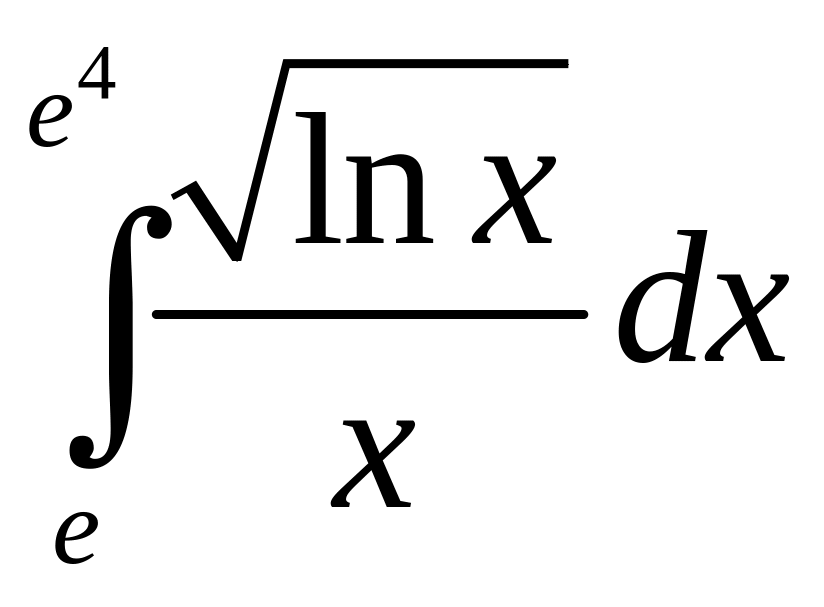 .
.а)
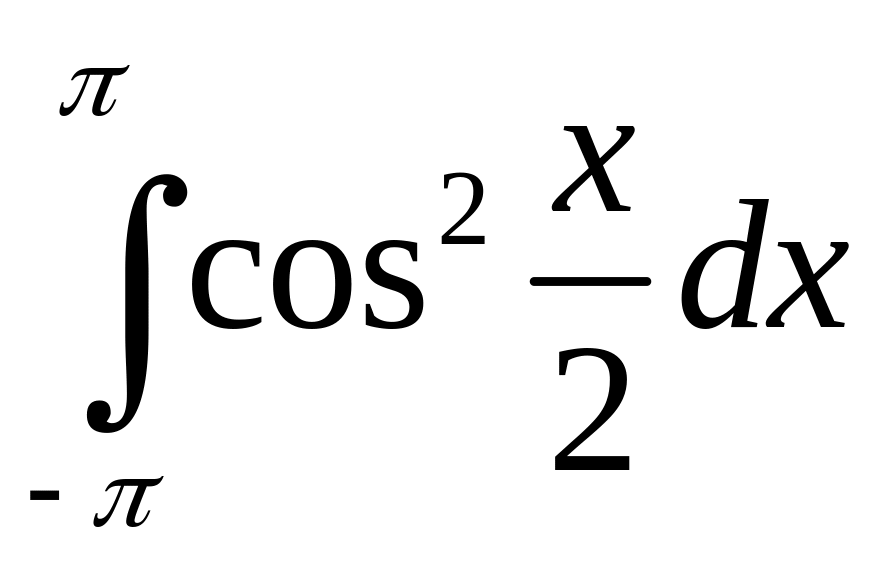 ;
б)
;
б)
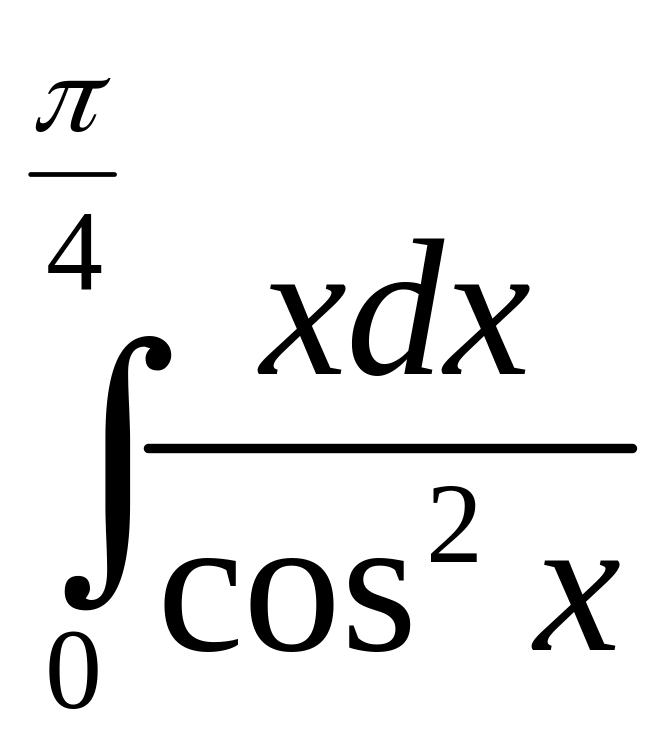 ;
в)
;
в)
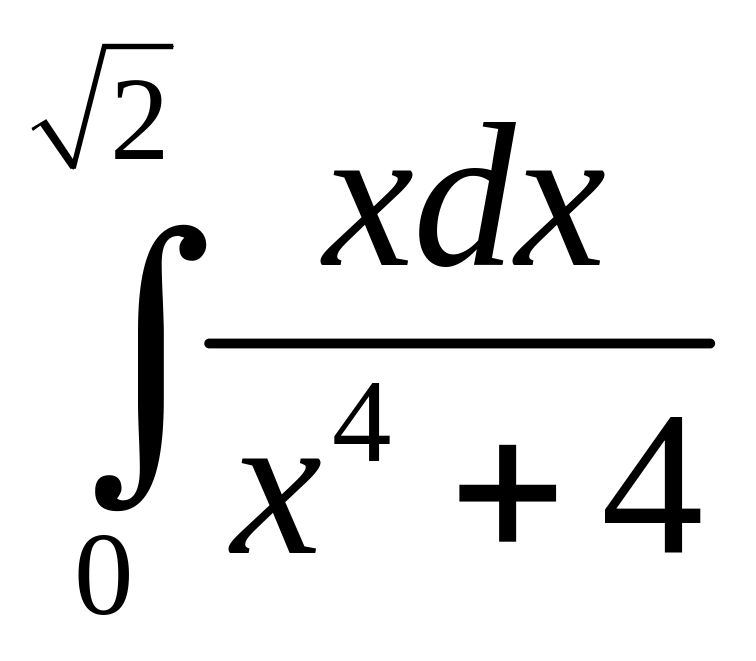 .
.а)
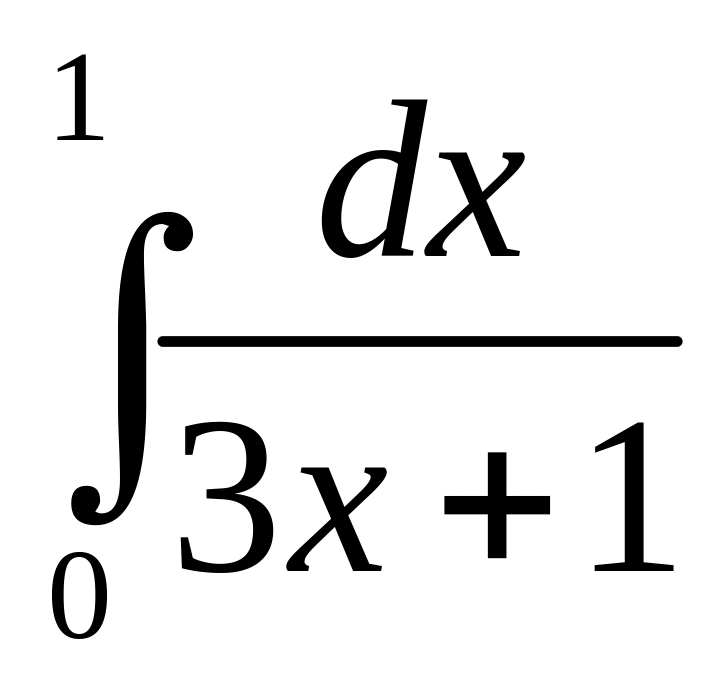 ;
б)
;
б)
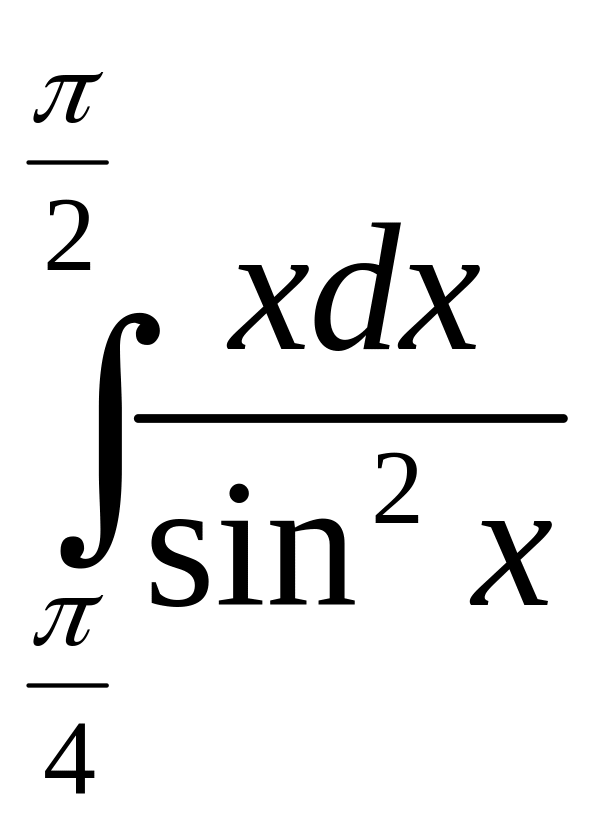 ;
в)
;
в)
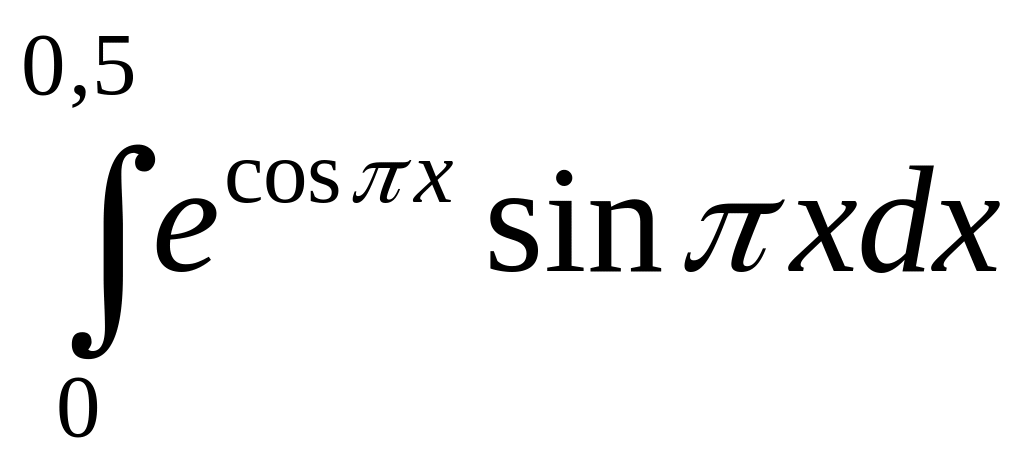 .
.а)
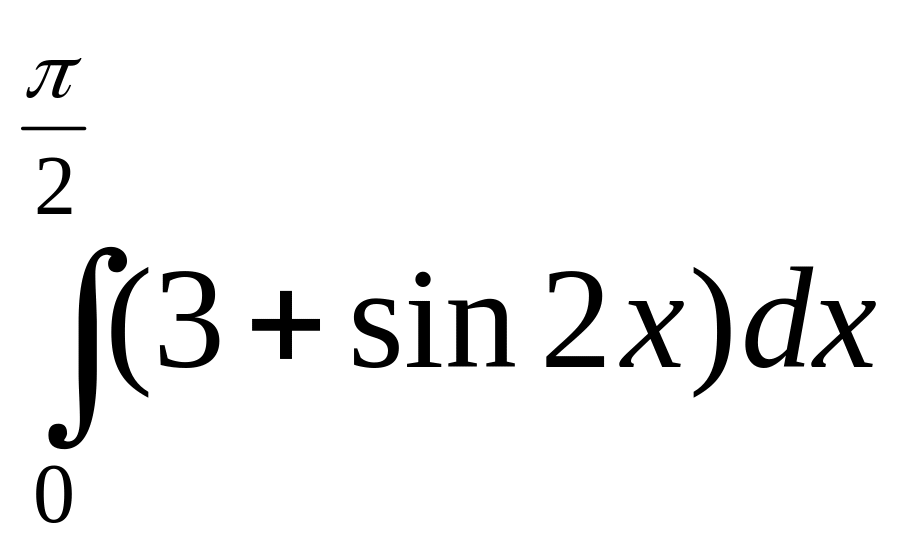 ;
б)
;
б)
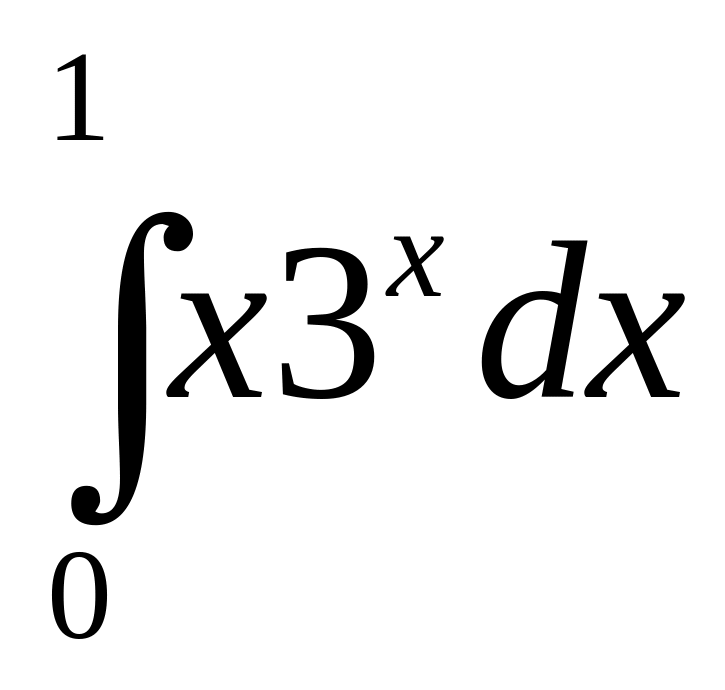 ;
в)
;
в)
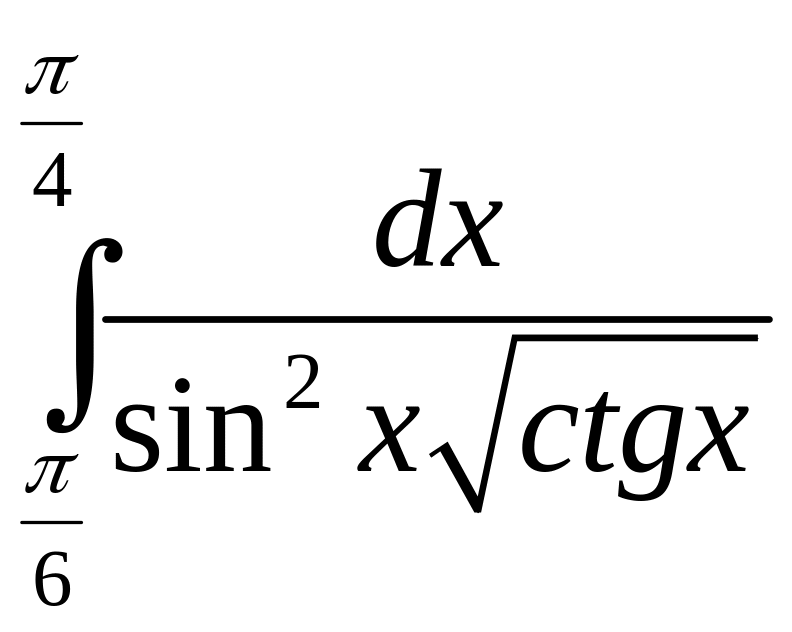 .
.а)
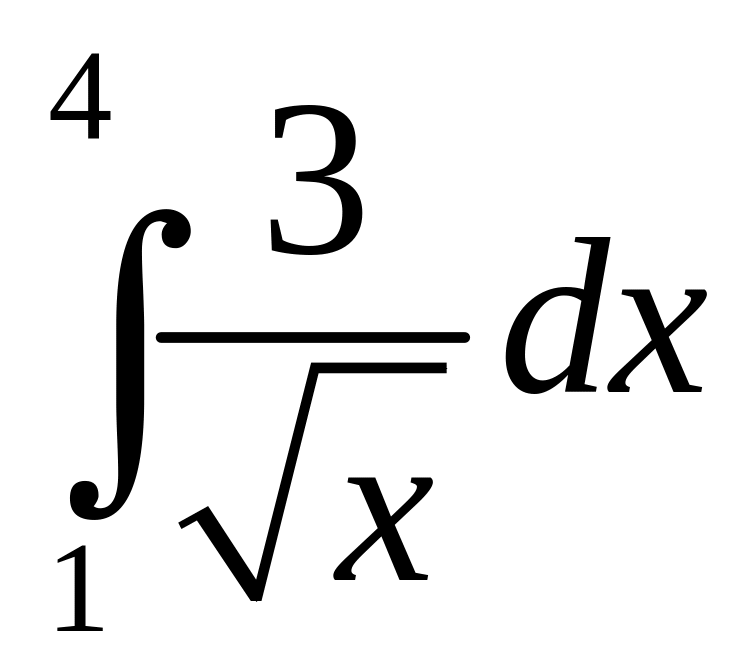 ;
б)
;
б)
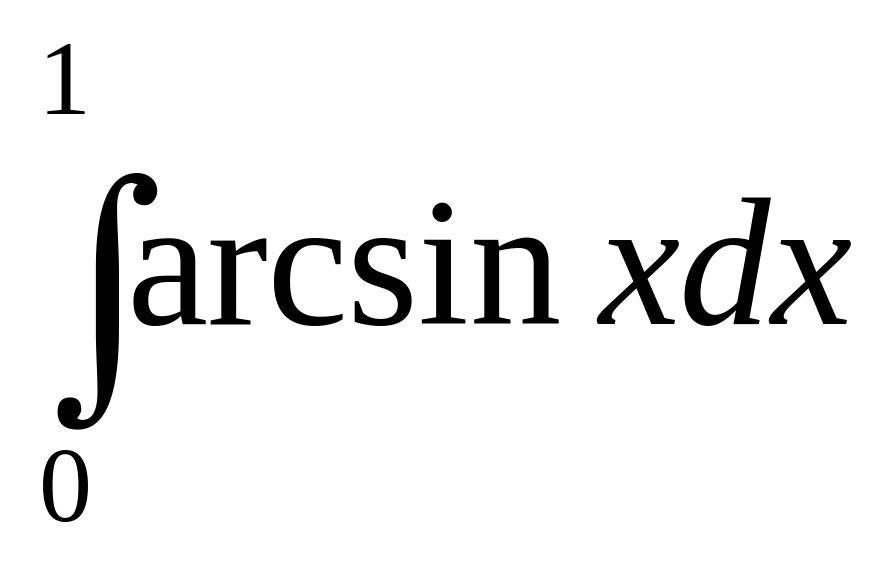 ;
в)
;
в)
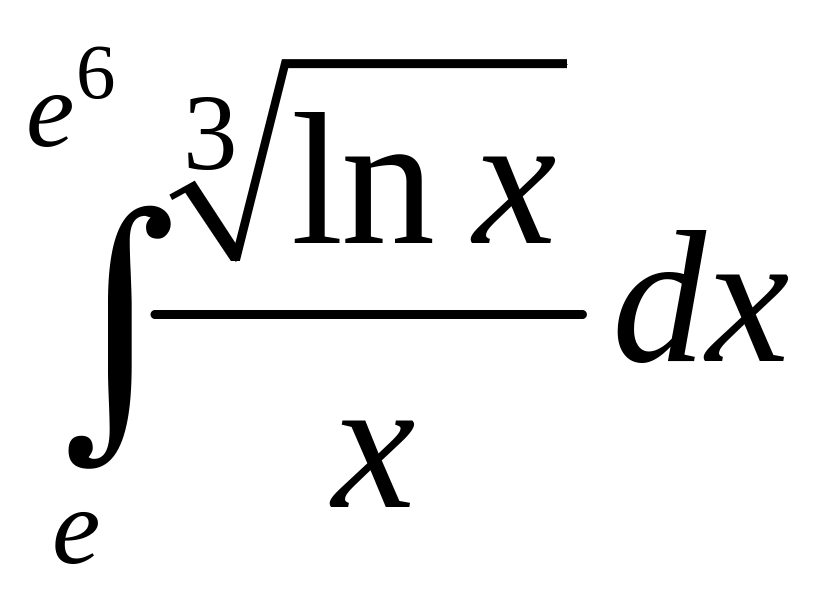 .
.а)
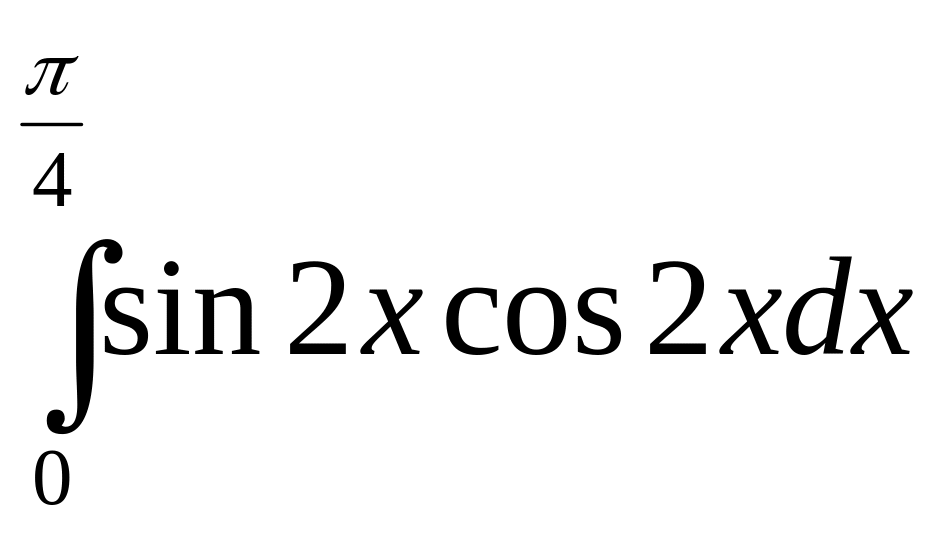 ;
б)
;
б)
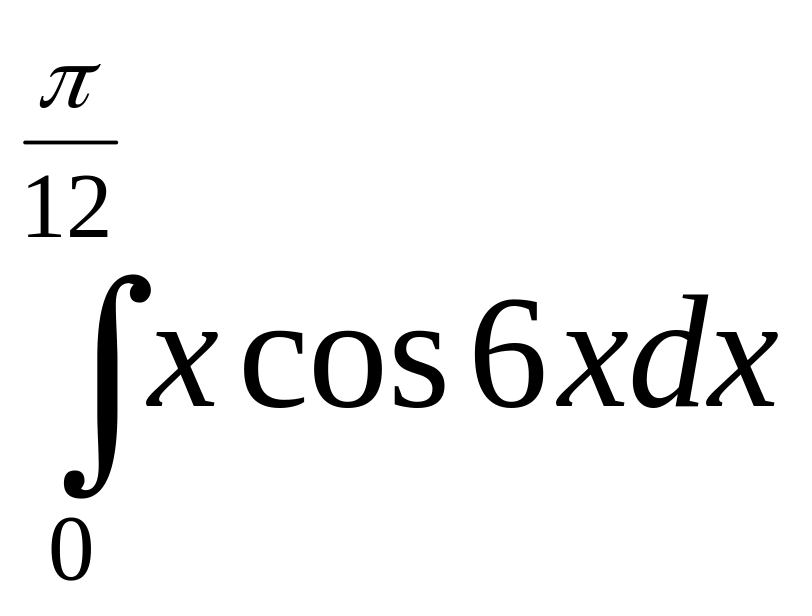 ;
в)
;
в)
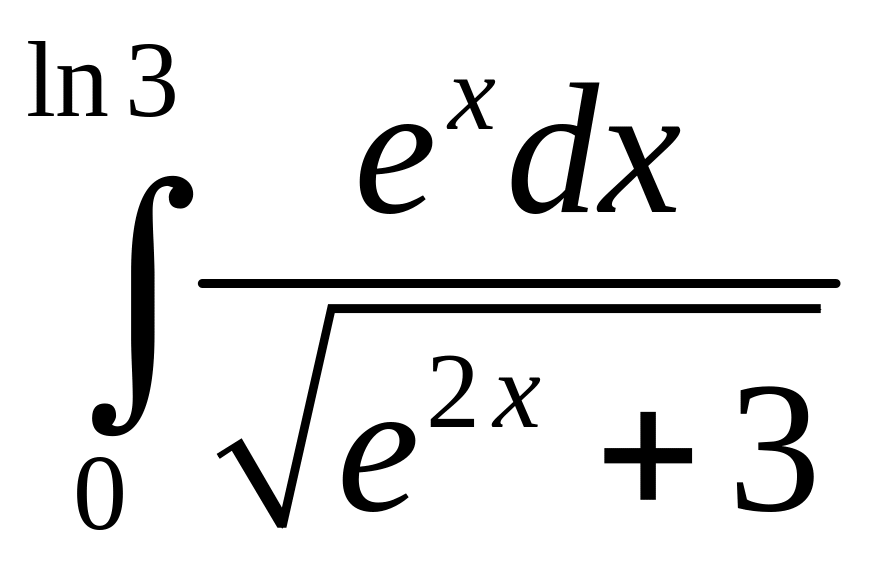 .
.а)
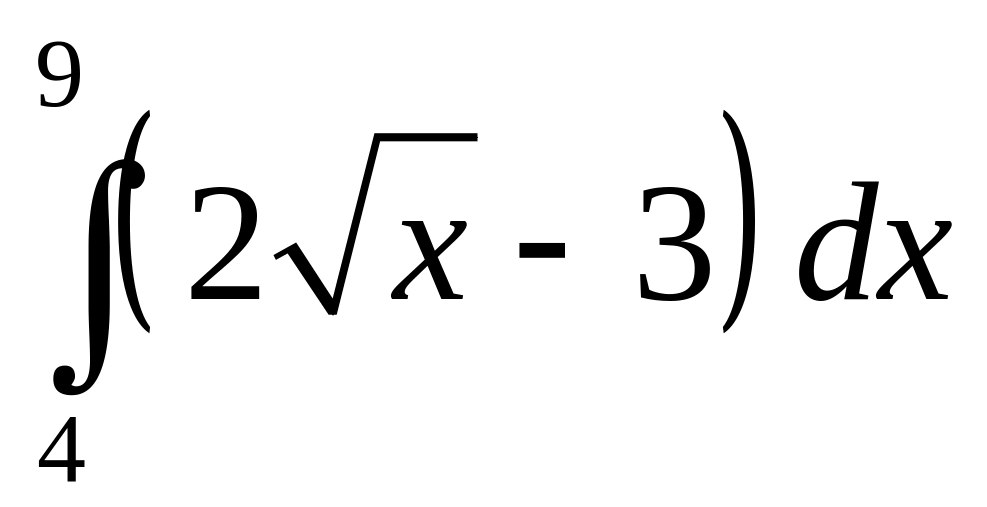 ;
б)
;
б)
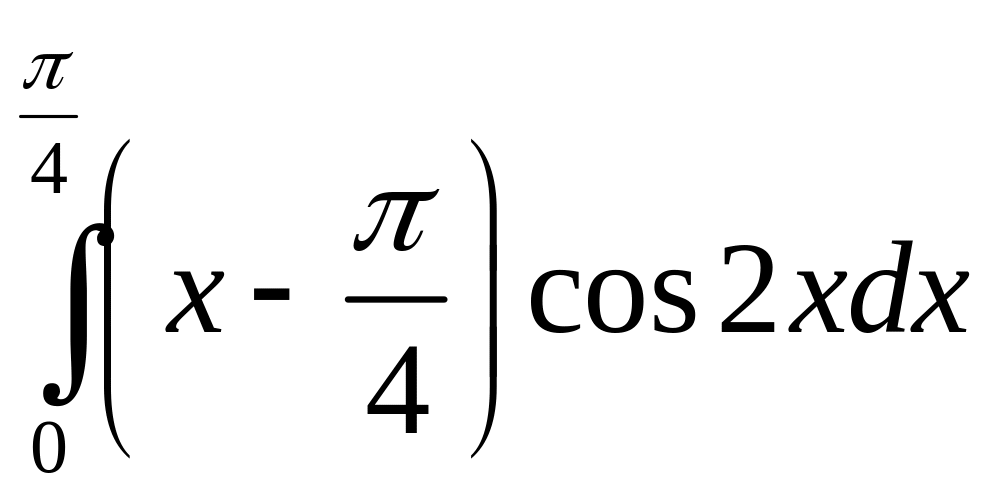 ;
в)
;
в)
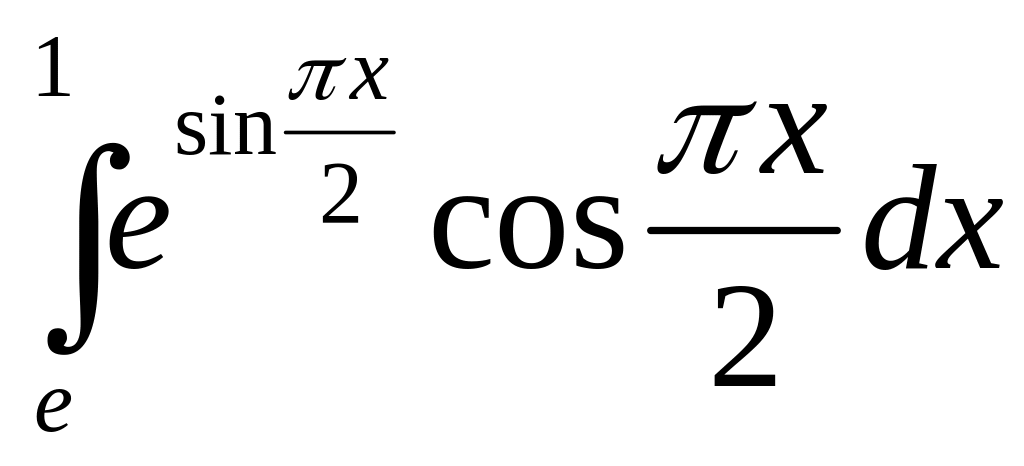 .
.а)
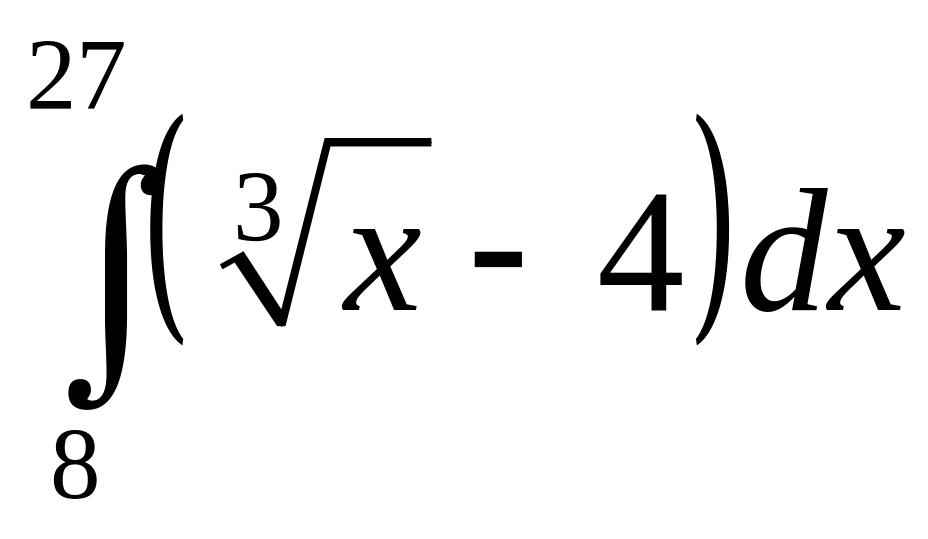 ;
б)
;
б)
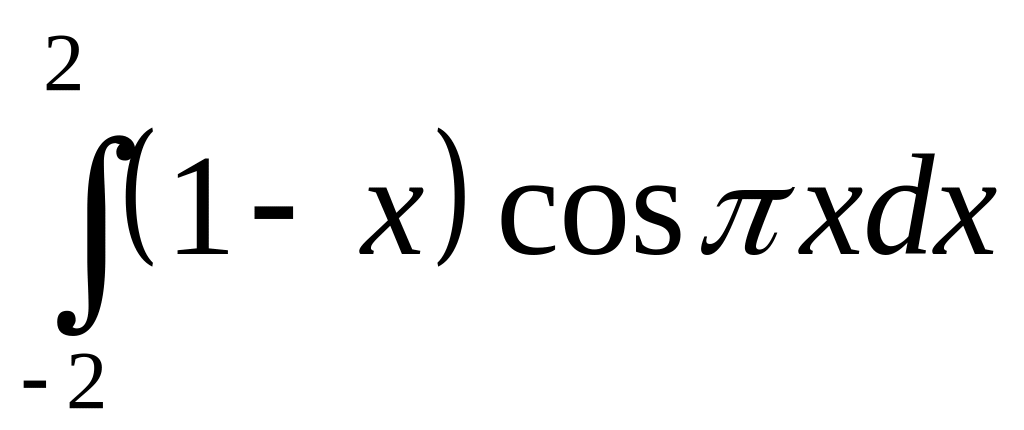 ;
в)
;
в)
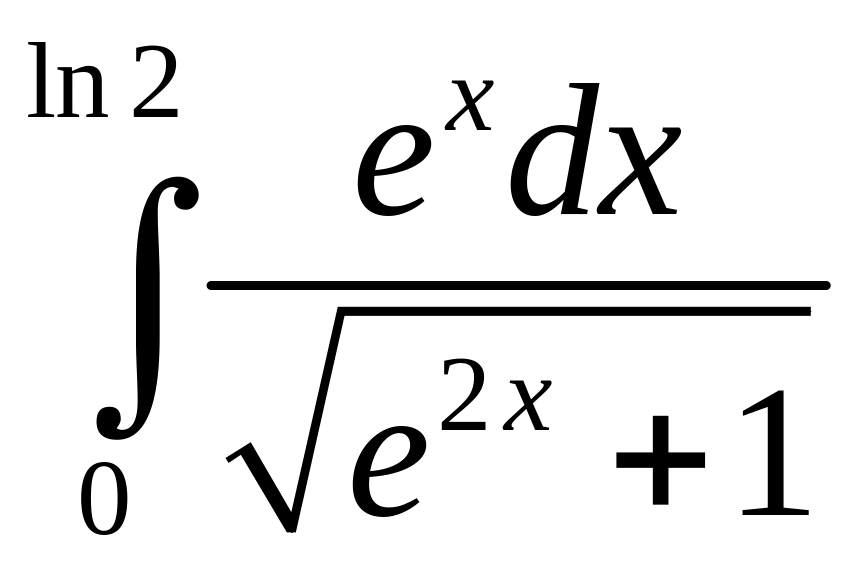 .
.а)
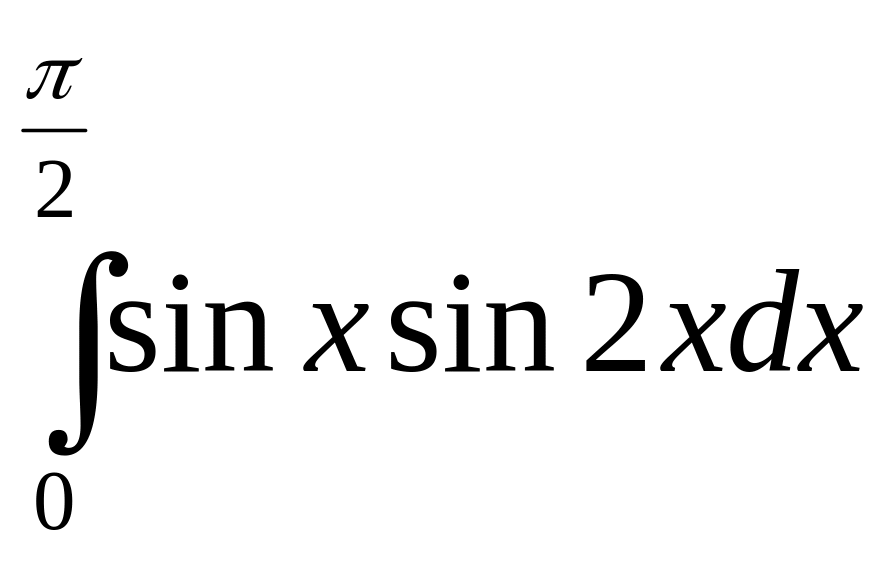 ;
б)
;
б)
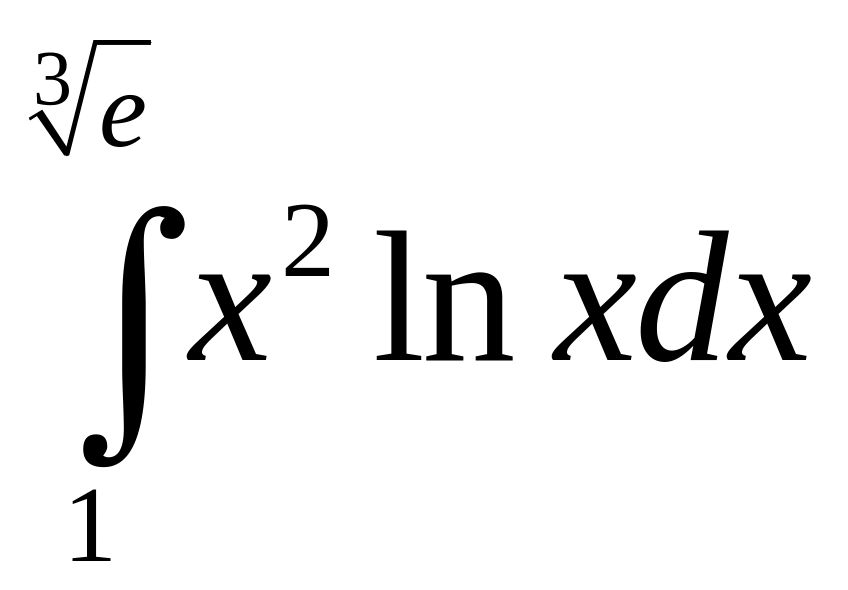 ;
в)
;
в)
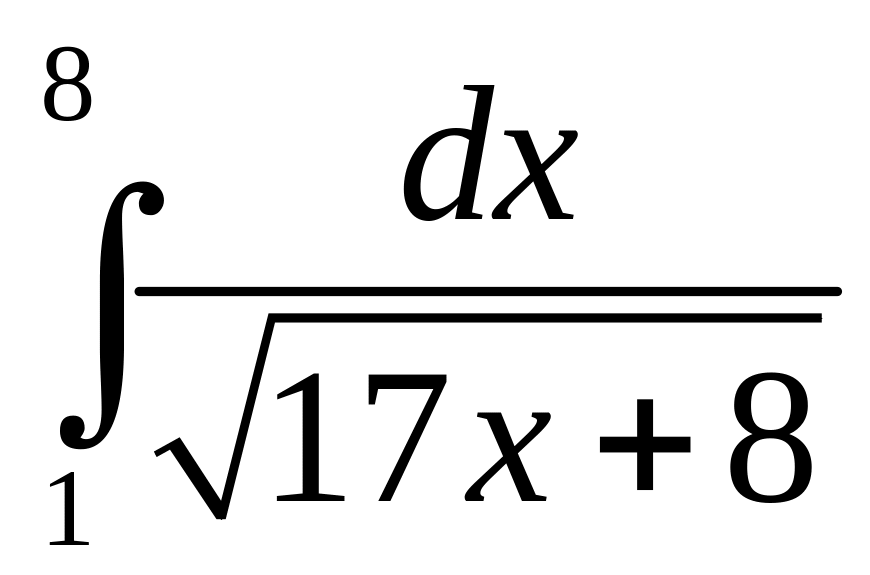 .
.а)
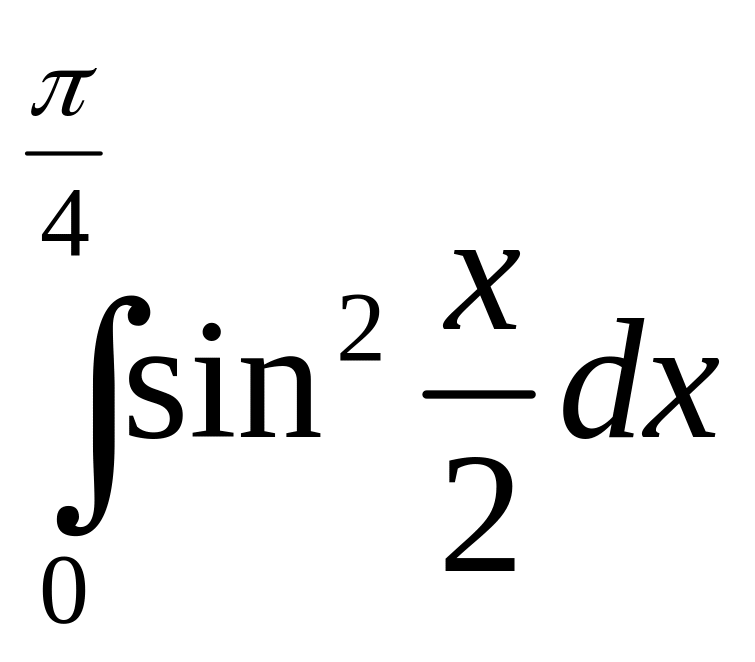 ;
б)
;
б)
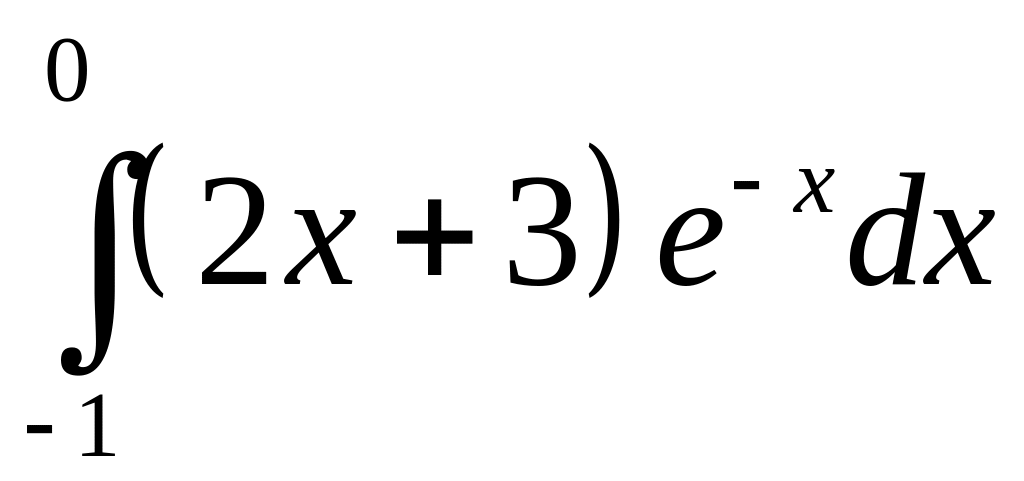 ;
в)
;
в)
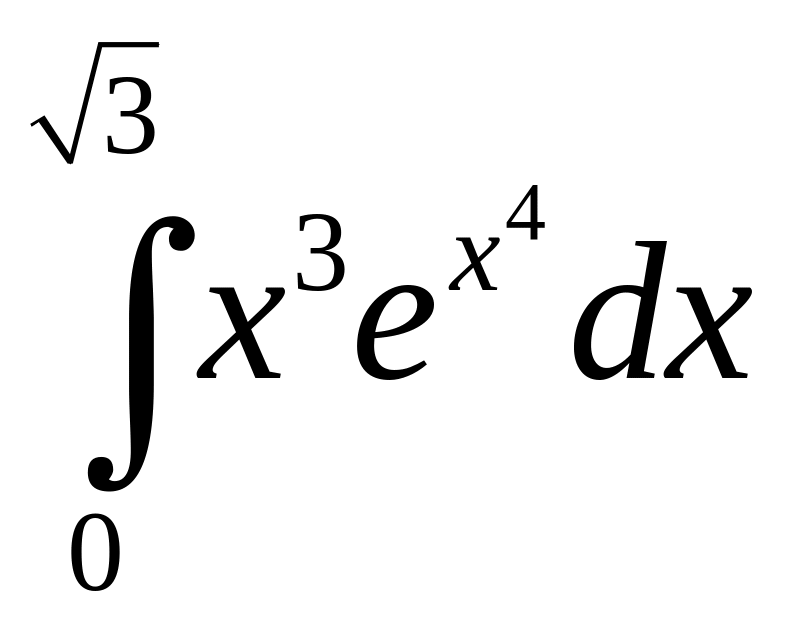 .
.а)
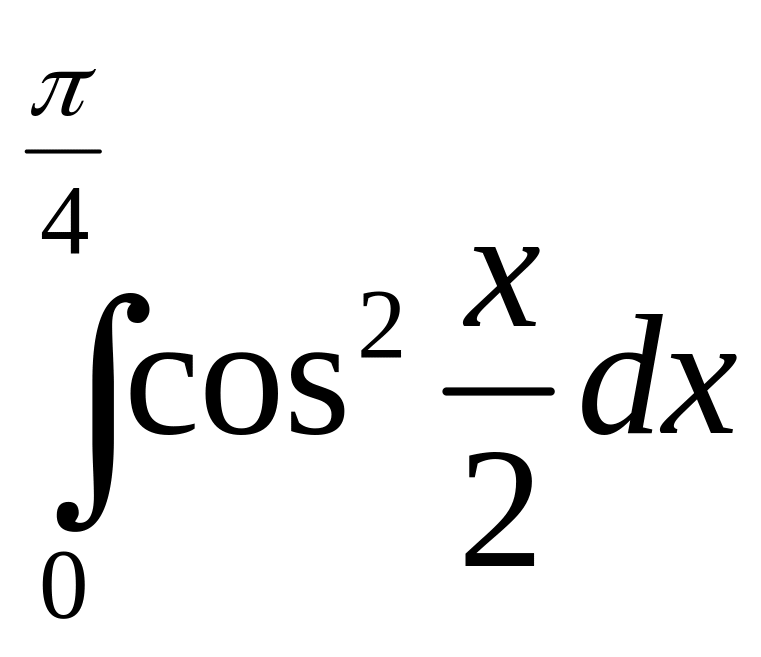 ;
б)
;
б)
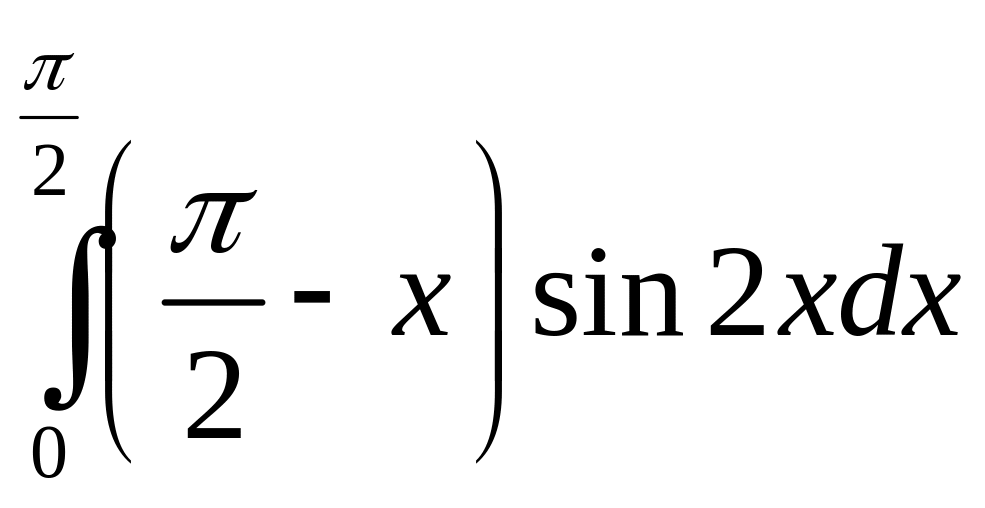 ;
в)
;
в)
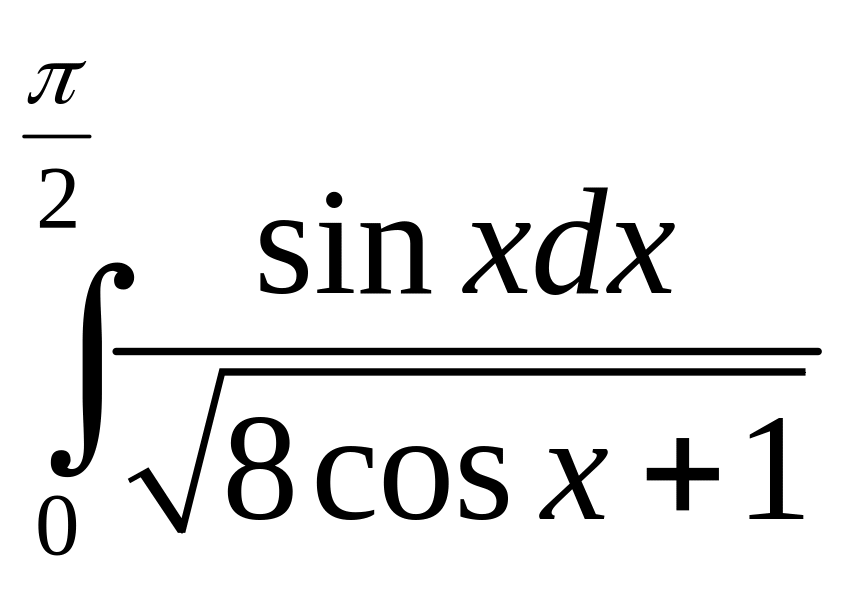 .
.а)
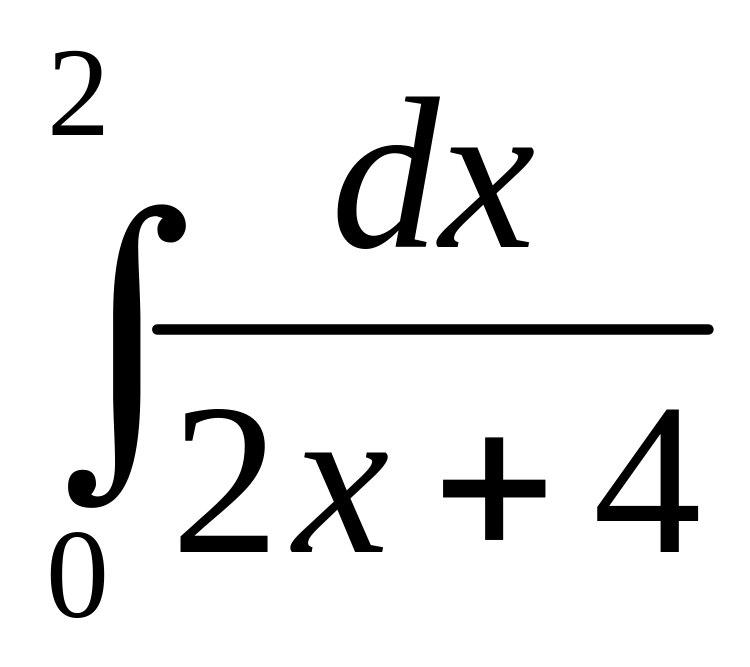 ;
б)
;
б)
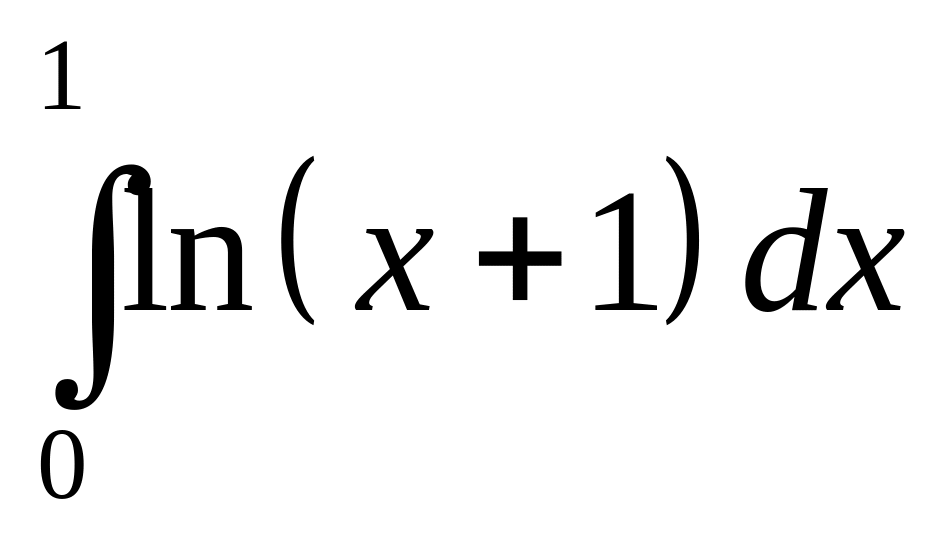 ;
в)
;
в)
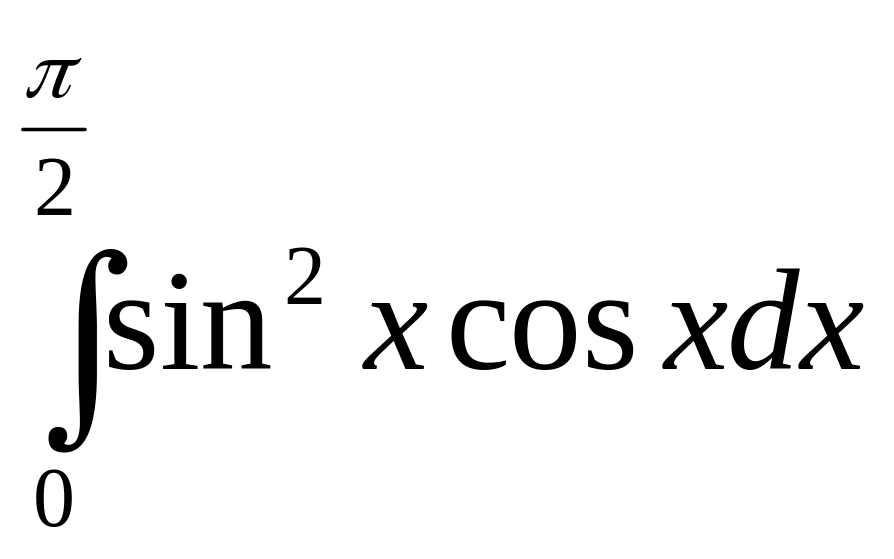 .
.а)
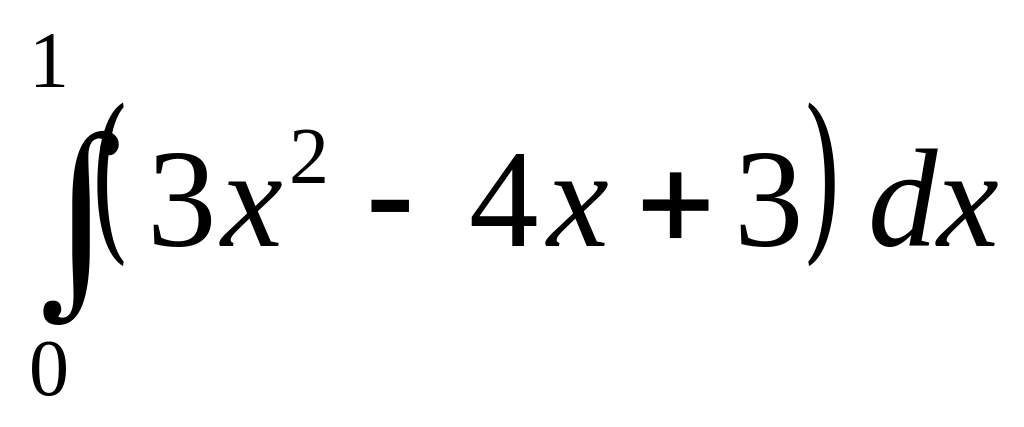 ;
б)
;
б)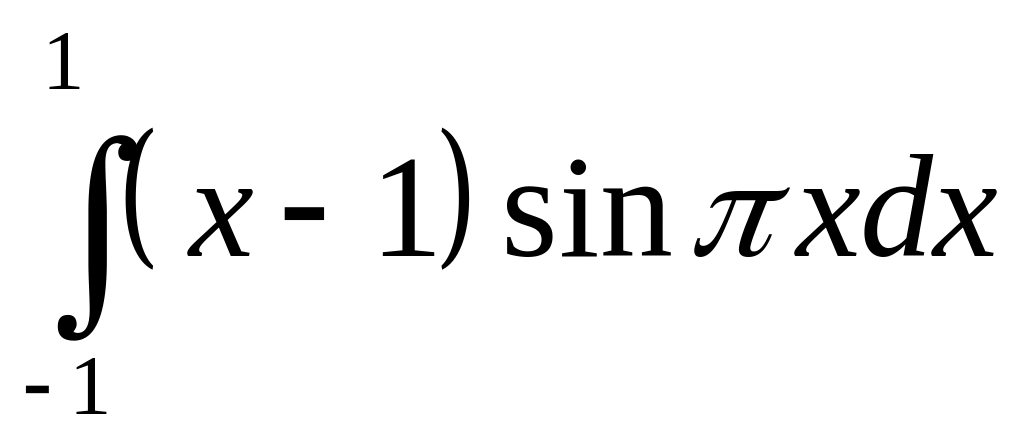 ;
в)
;
в)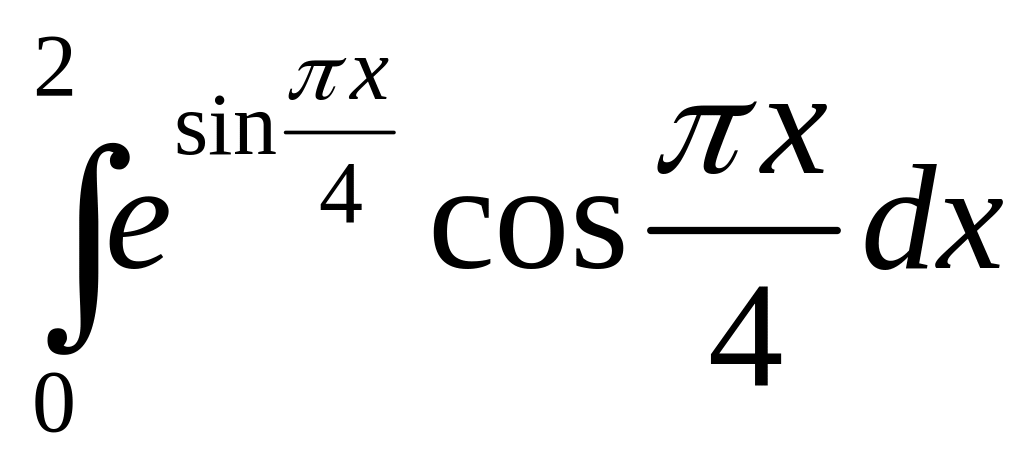 .
.а)
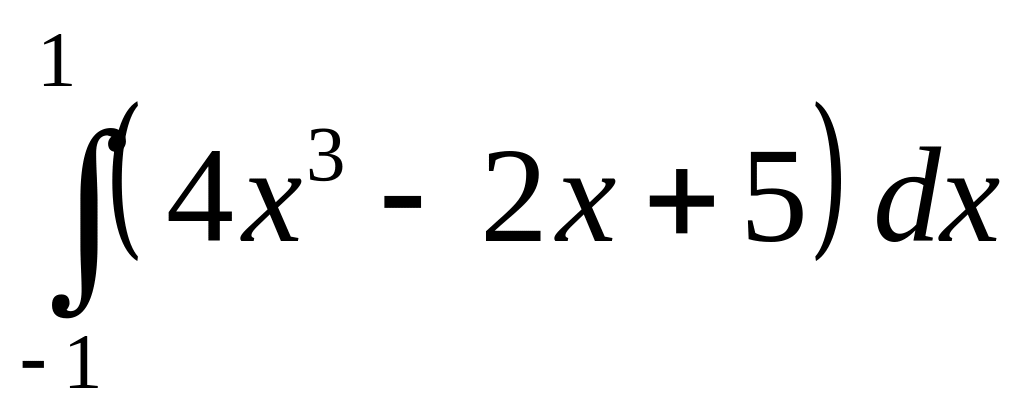 ;
б)
;
б)
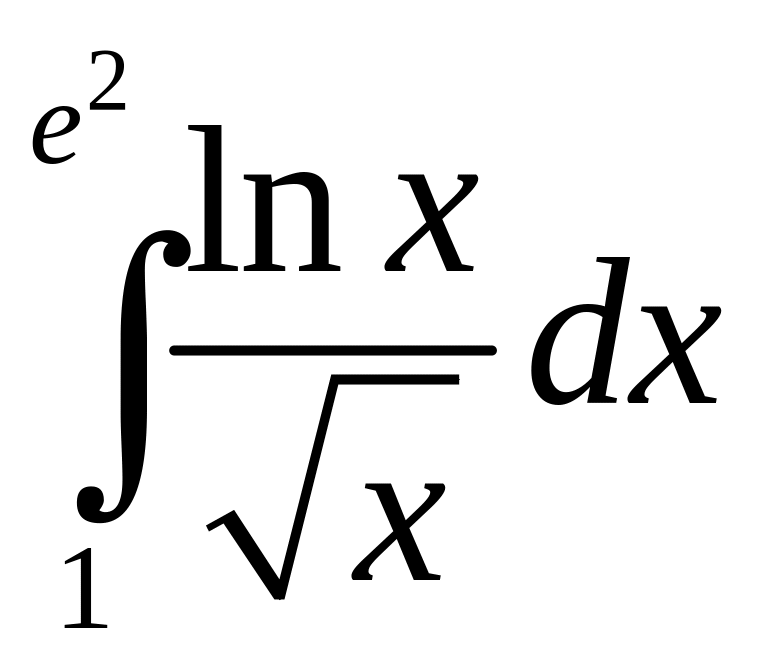 ;
в)
;
в)
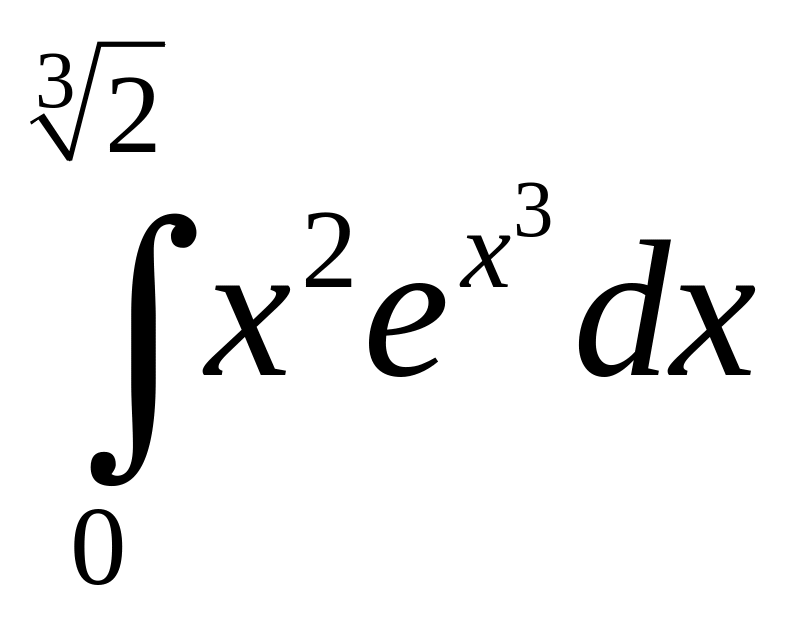 .
.а)
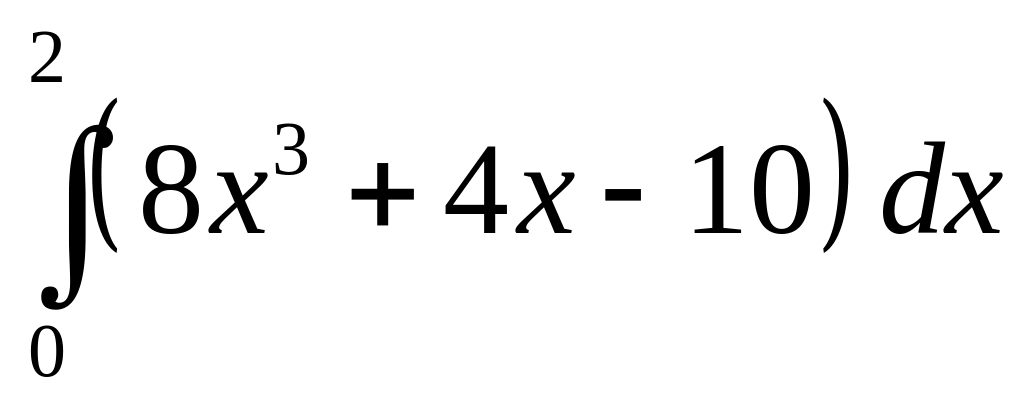 ;
б)
;
б)
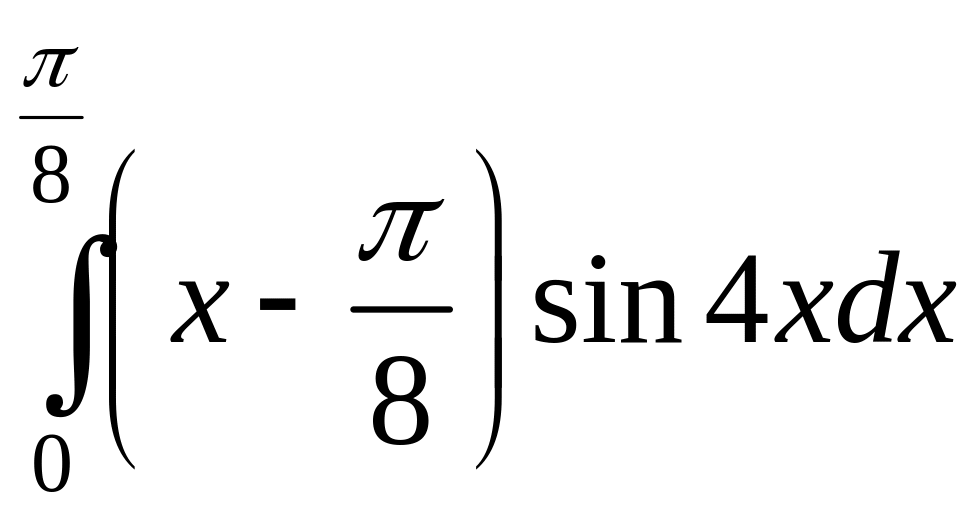 ;
в)
;
в)
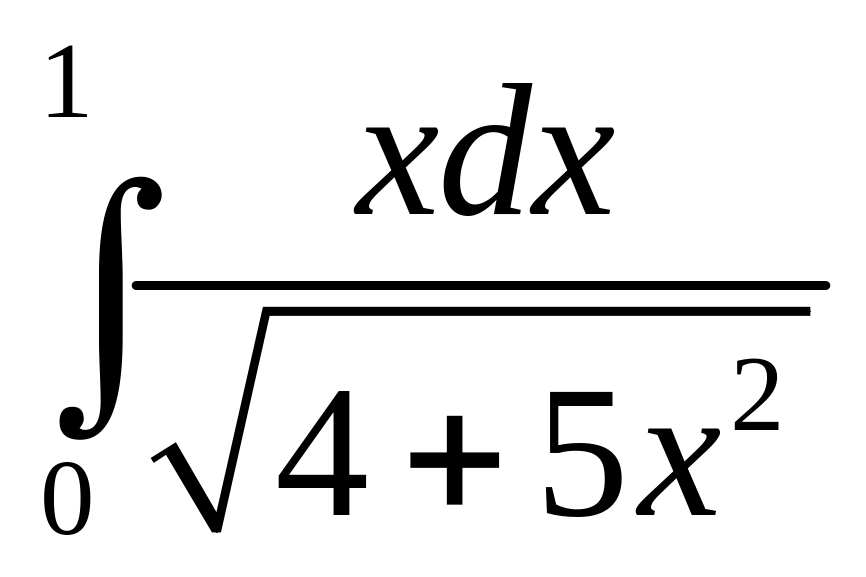 .
.а)
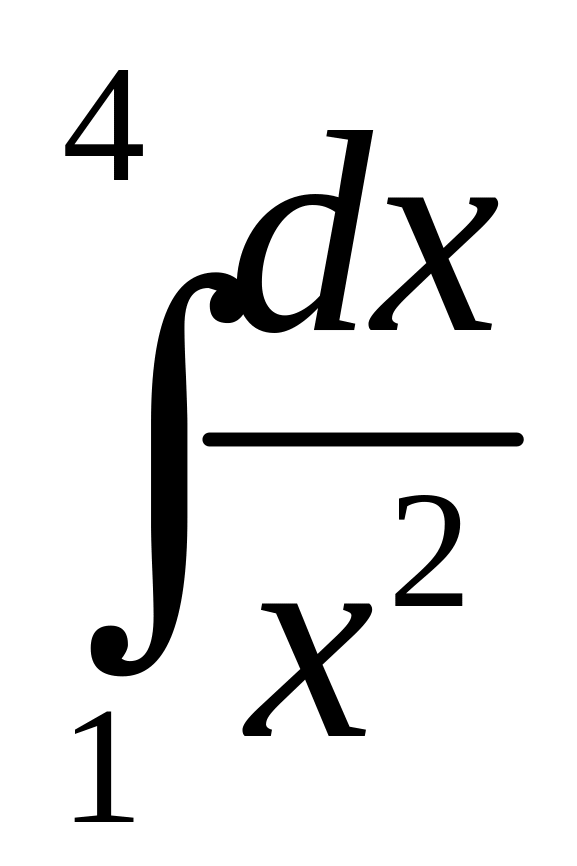 ;
б)
;
в)
;
б)
;
в)
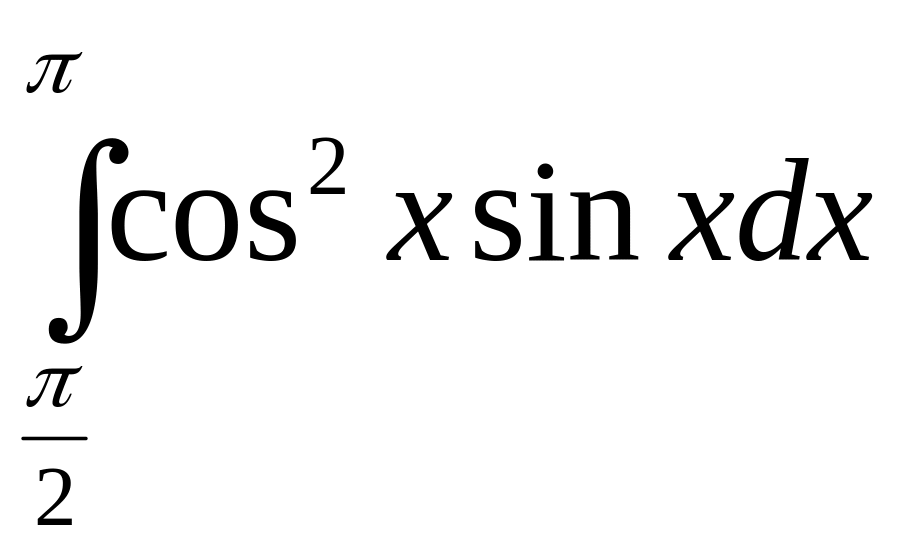 .
.а)
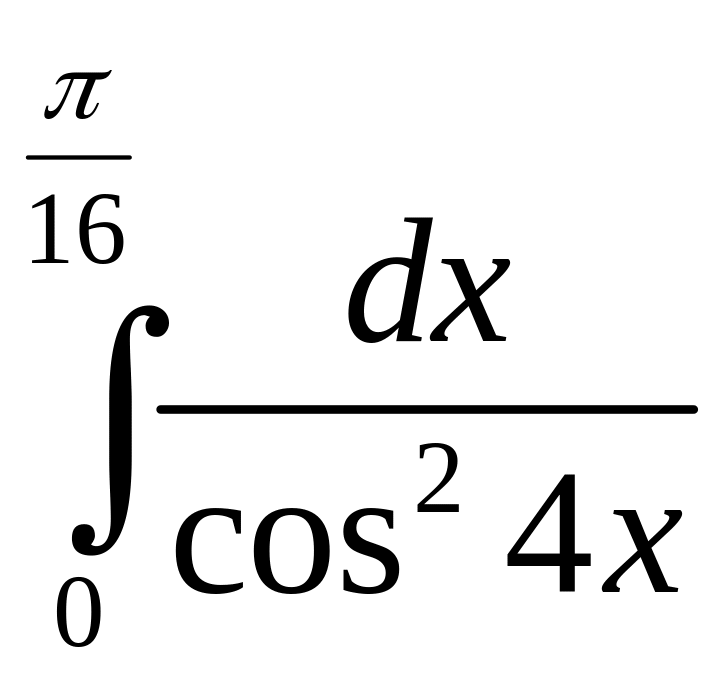 ;
б)
;
в)
;
б)
;
в)
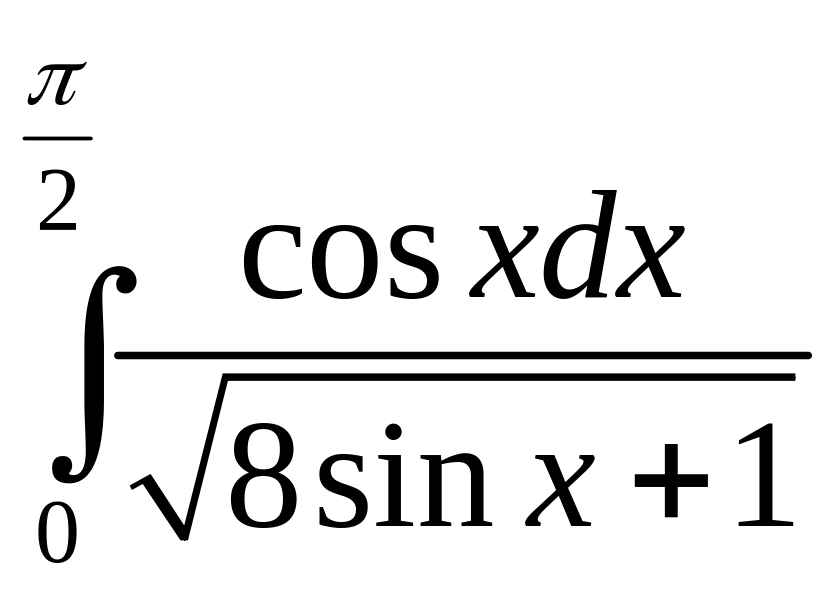 .
.а)
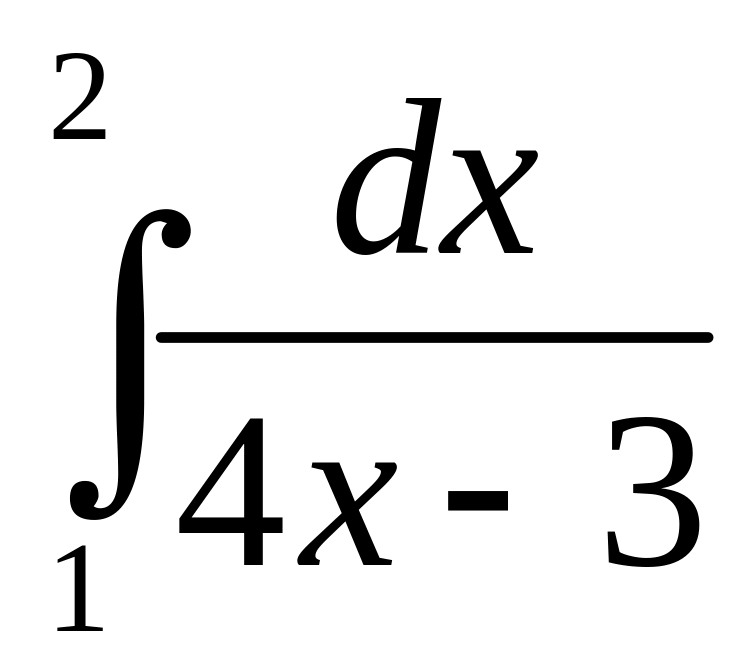 ;
б)
;
б)
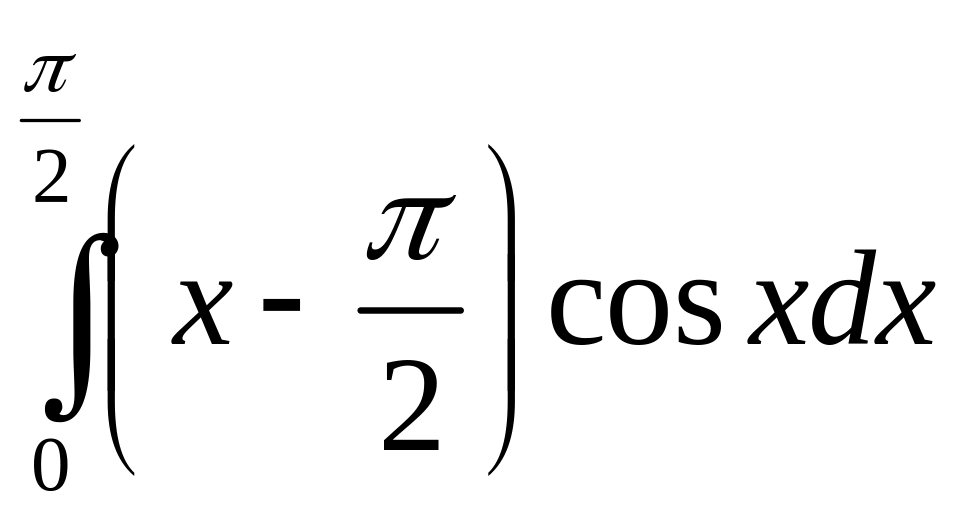 ;
в)
;
в)
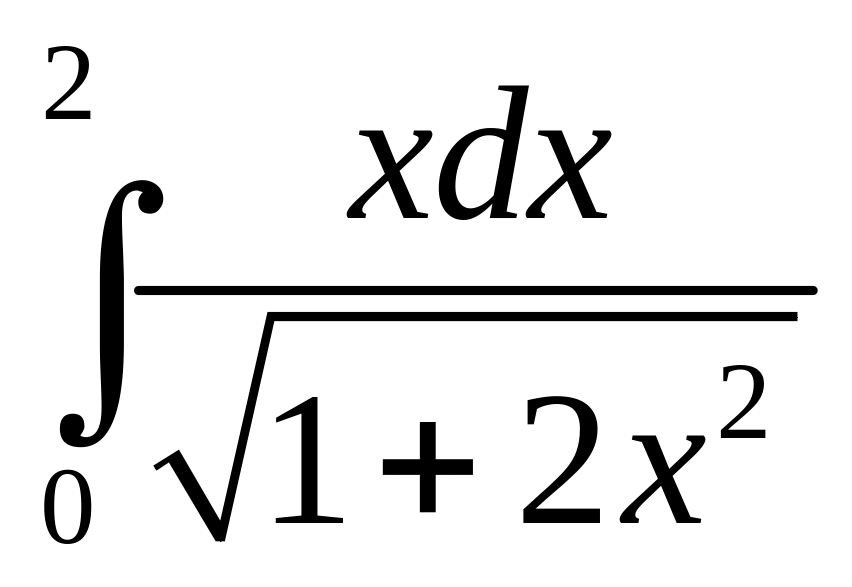 .
.а)
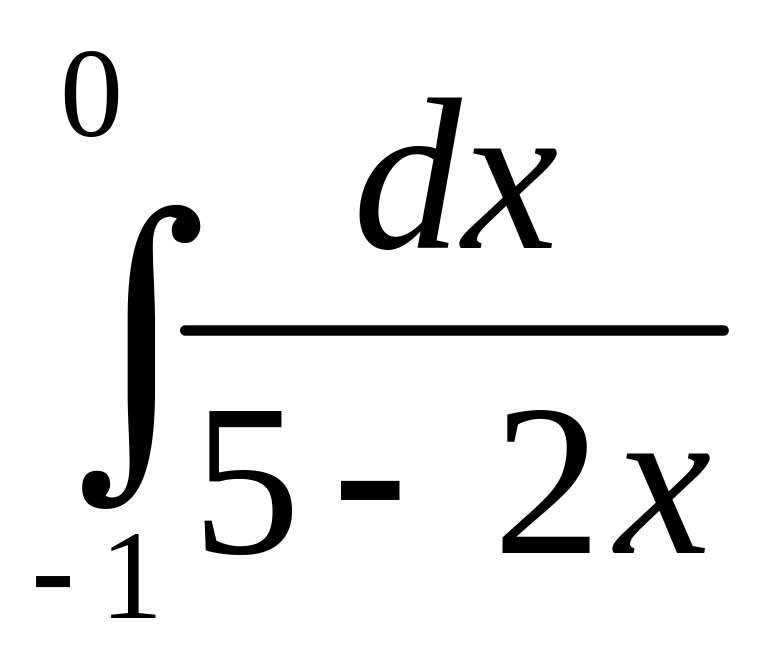 ;
б)
;
б)
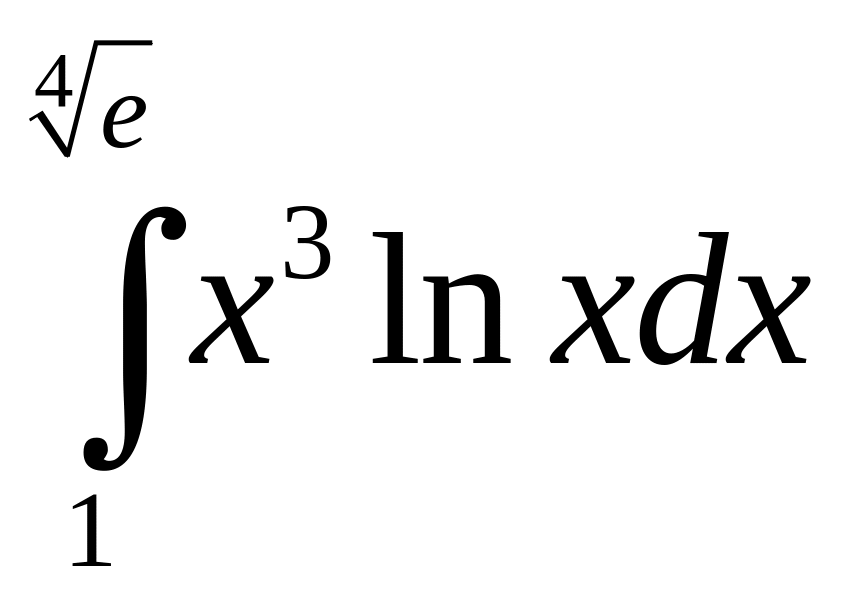 ;
в)
;
в)
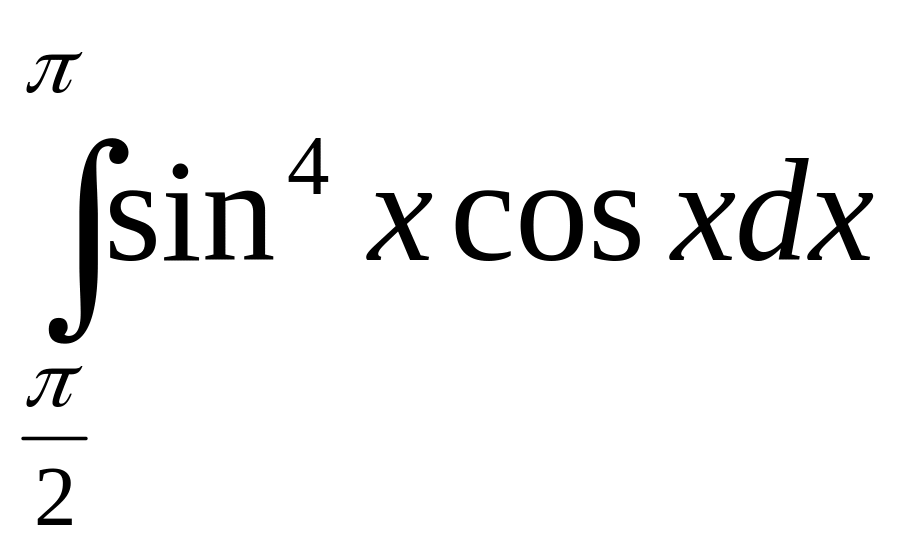 .
.а)
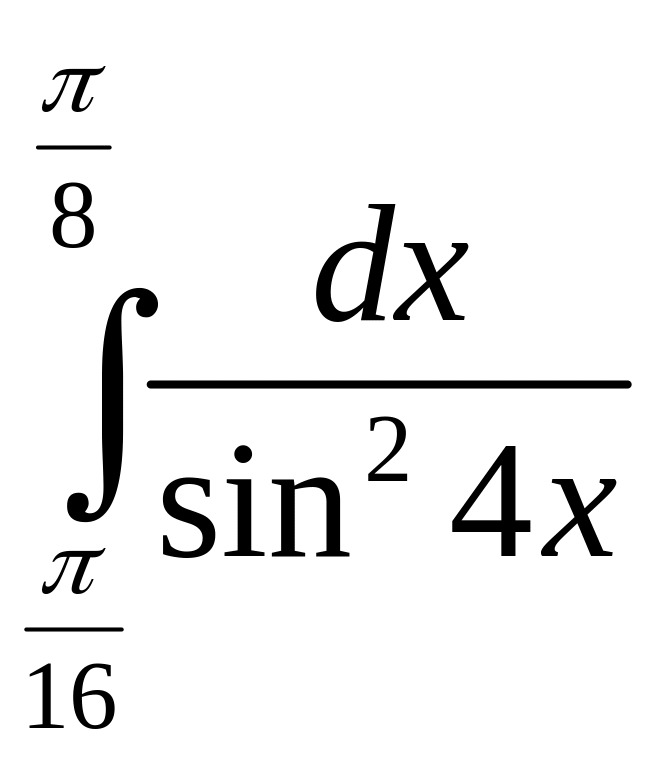 ;
б)
;
б)
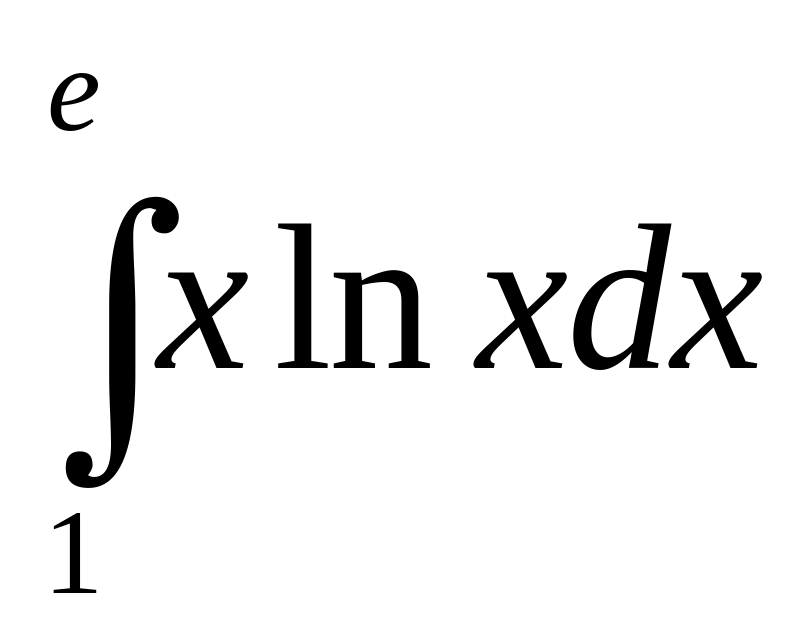 ;
в)
;
в)
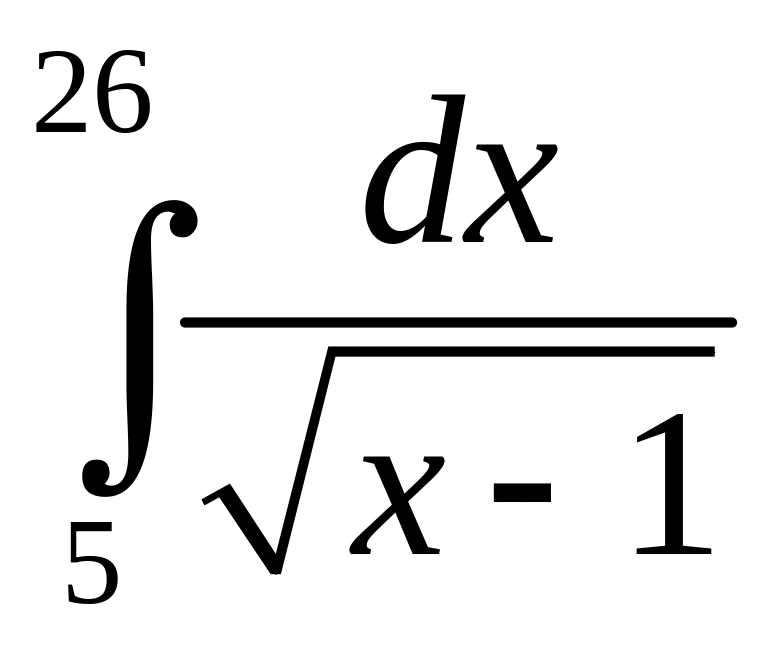 .
.а)
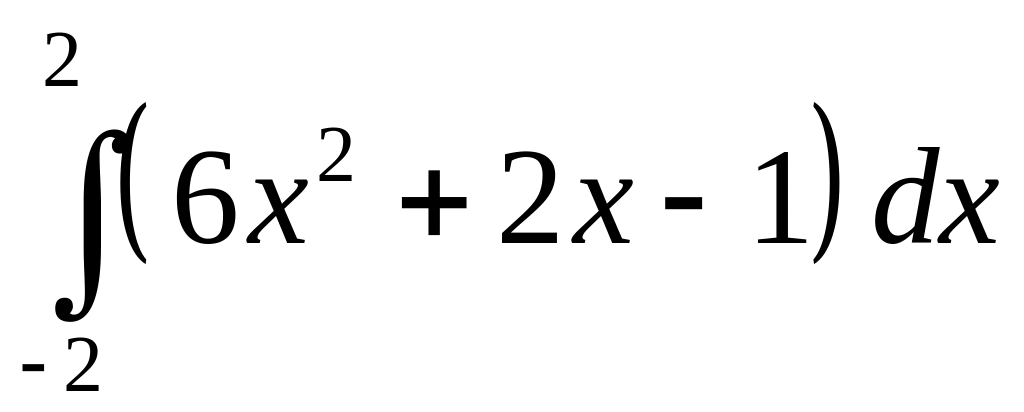 ;
б)
;
б)
 ;
в)
;
в)
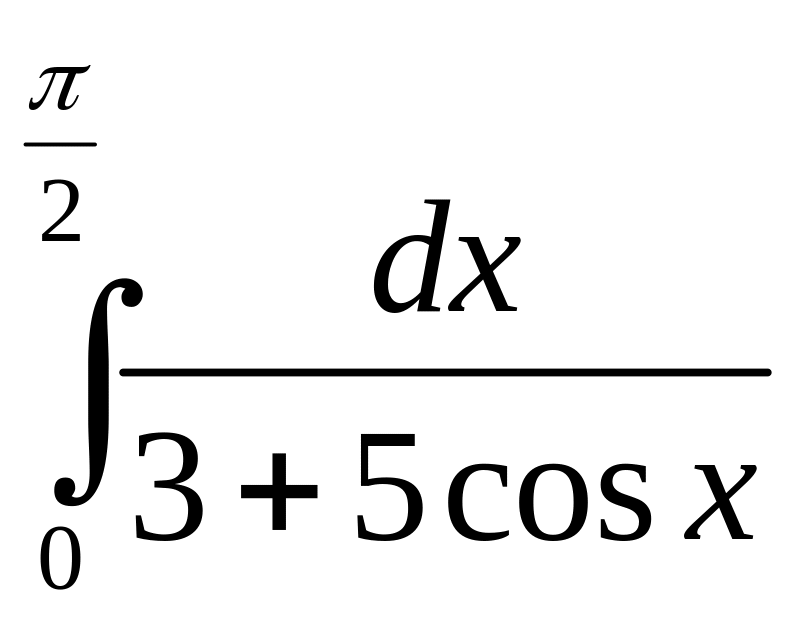 .
.а)
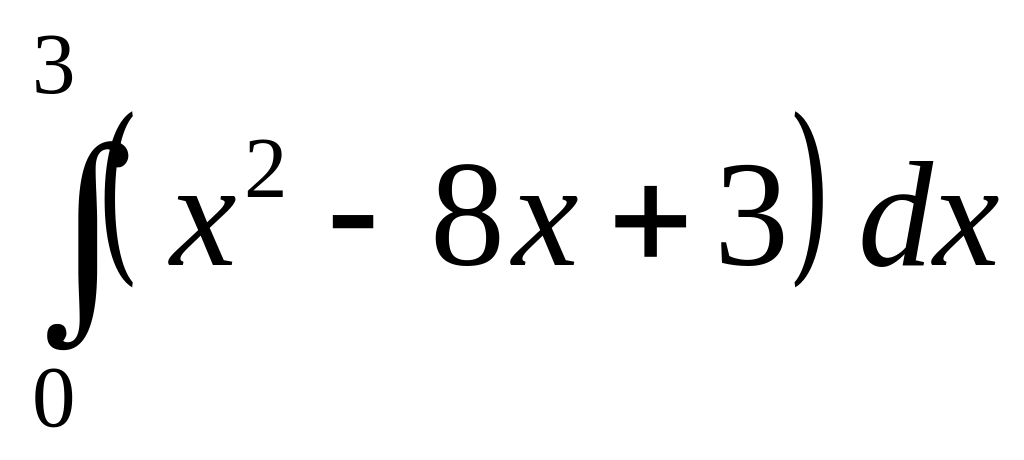 ;
б)
;
б)
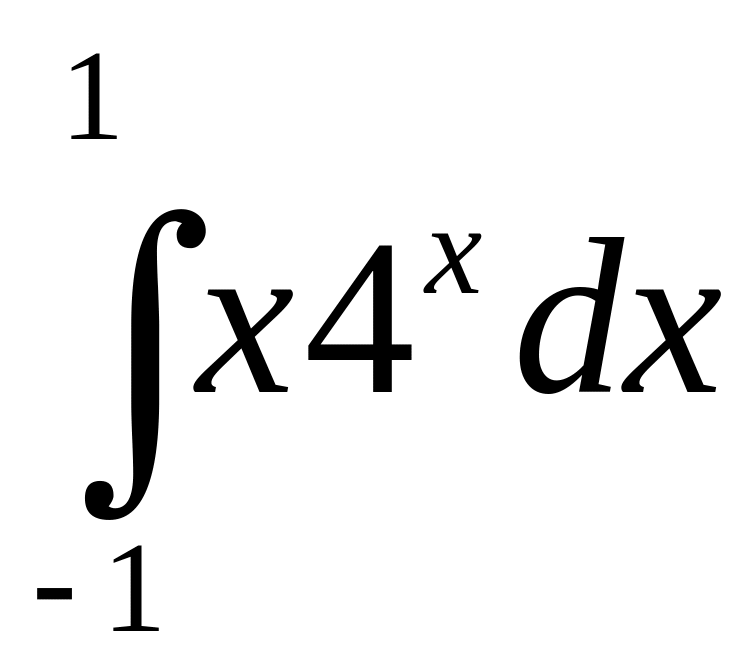 ;
в)
;
в)
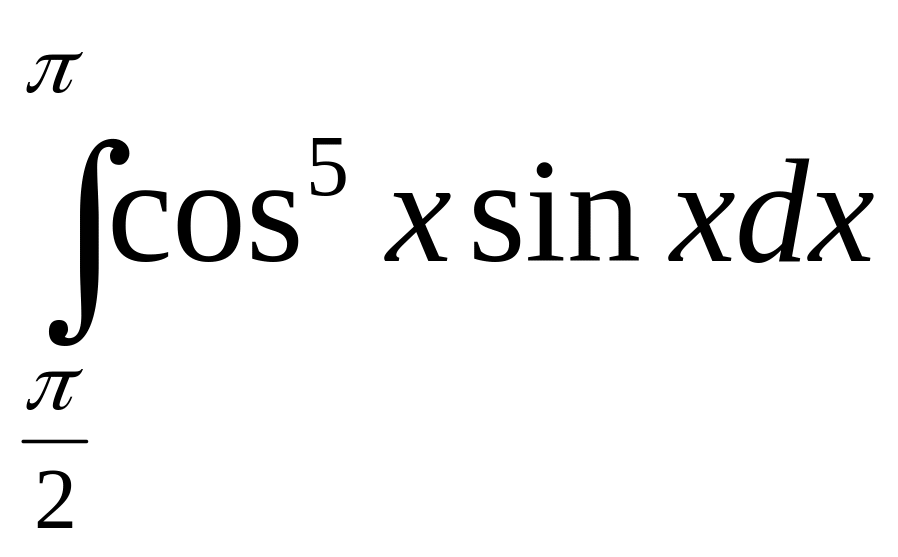 .
.а)
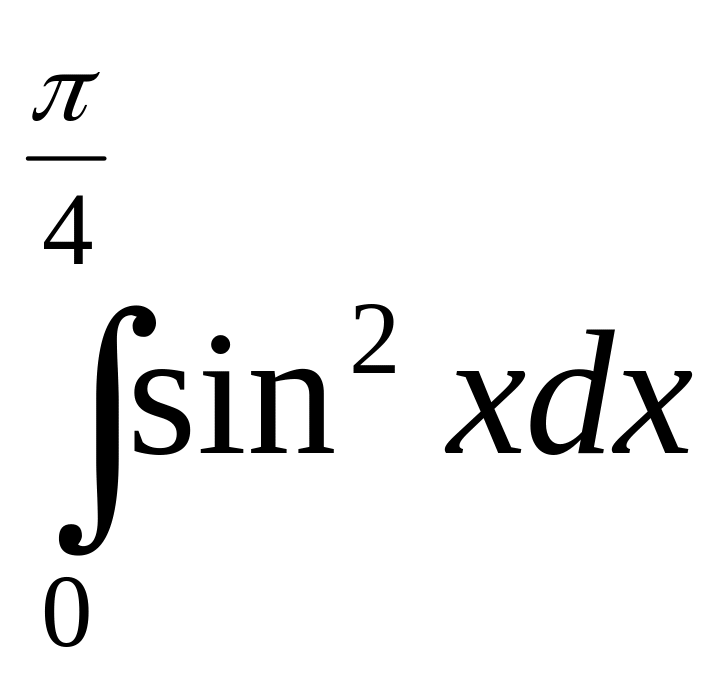 ;
б)
;
б)
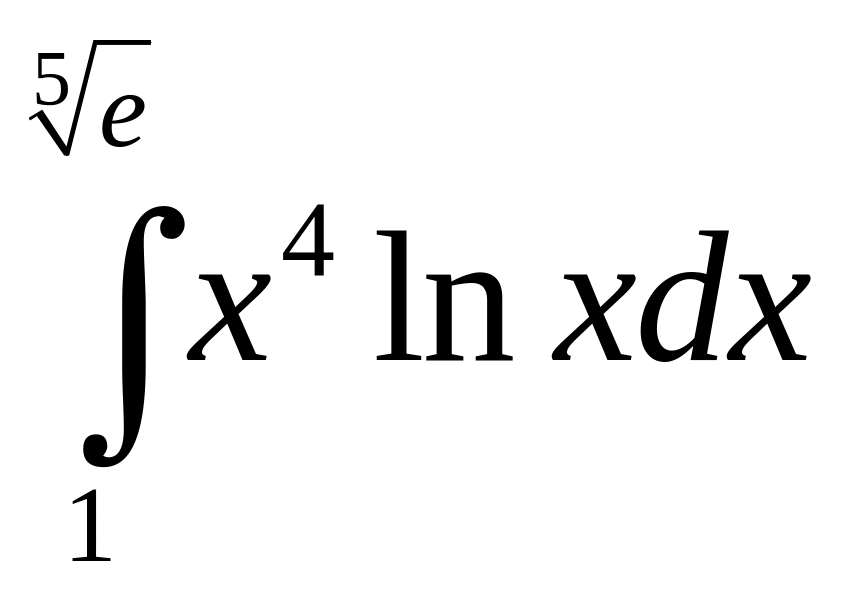 ;
в)
;
в)
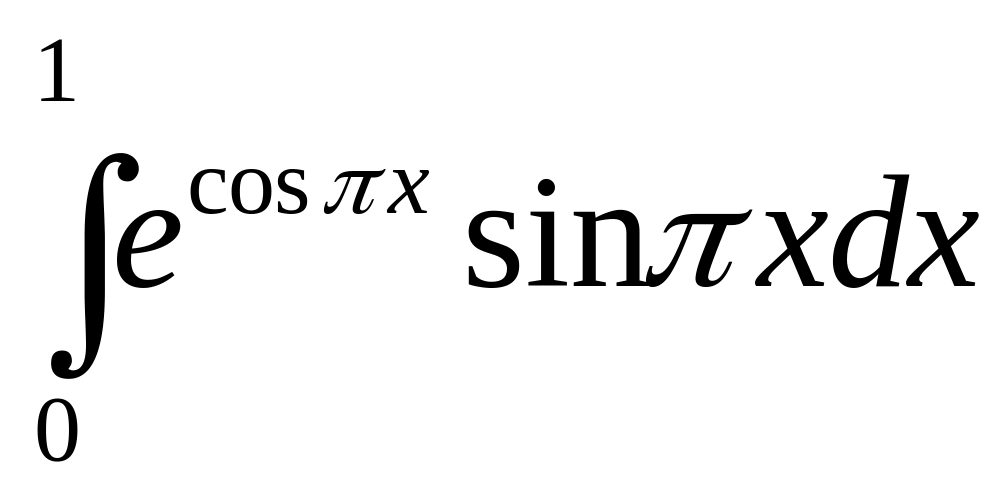 .
.а)
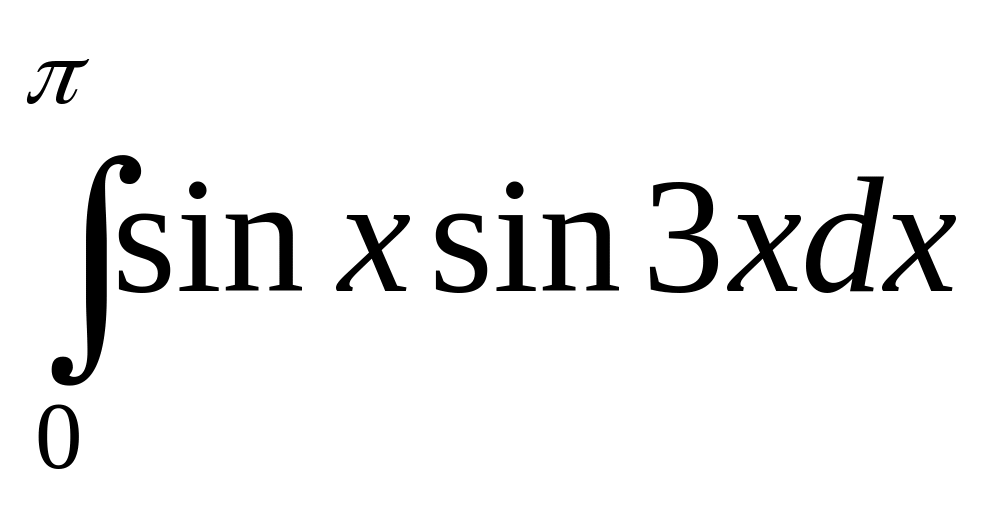 ;
б)
;
б)
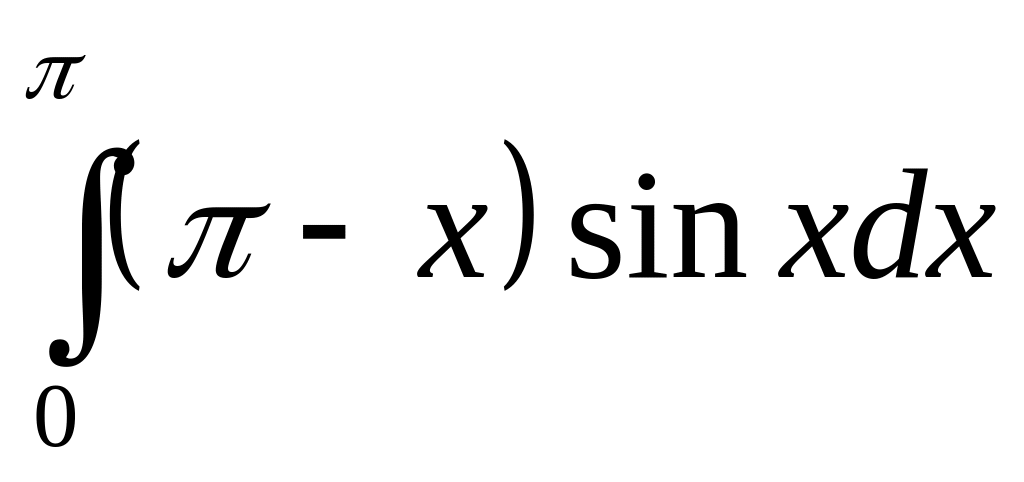 ;
в)
;
в)
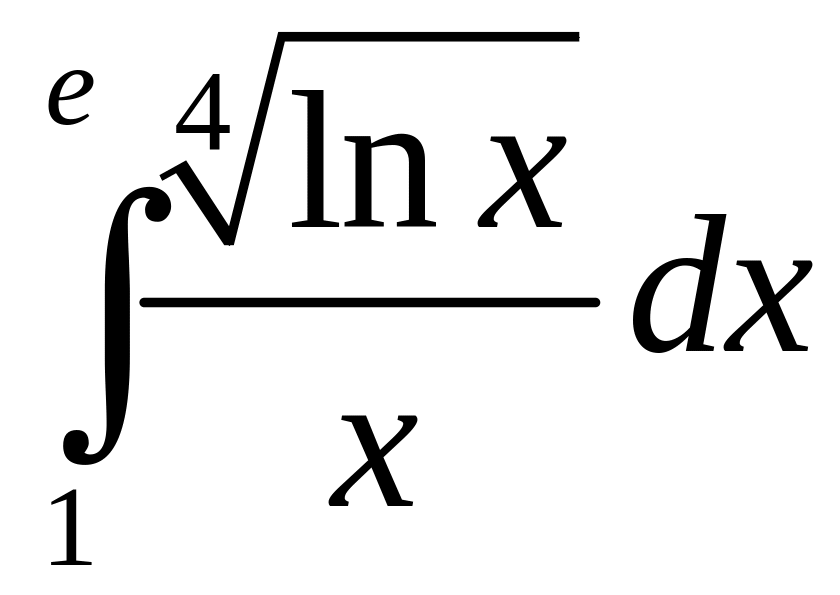 .
.
X. Вычислить:
- площадь фигуры,
ограниченной параболой
![]() и прямой
и прямой
![]() ;
;
- объем тела,
образованного вращением вокруг оси
фигуры, ограниченной параболой
и прямой
(значения параметров
![]() приведены
в таблице) .
приведены
в таблице) .
№ варианта |
|
|
|
|
|
1 |
1 |
3 |
3 |
2 |
5 |
2 |
3 |
1 |
4 |
-1 |
9 |
3 |
3 |
-4 |
3 |
-2 |
8 |
4 |
2 |
3 |
5 |
4 |
11 |
5 |
2 |
-2 |
2 |
-3 |
8 |
6 |
1 |
4 |
5 |
2 |
5 |
7 |
1 |
-4 |
5 |
-2 |
8 |
8 |
2 |
-5 |
7 |
-4 |
10 |
9 |
3 |
-4 |
2 |
-3 |
6 |
10 |
1 |
6 |
10 |
-1 |
18 |
11 |
1 |
3 |
3 |
3 |
7 |
12 |
3 |
1 |
4 |
-3 |
3 |
13 |
3 |
-5 |
4 |
-1 |
3 |
14 |
2 |
3 |
5 |
-2 |
12 |
15 |
2 |
5 |
7 |
4 |
8 |
16 |
1 |
4 |
5 |
2 |
8 |
17 |
1 |
-4 |
5 |
-3 |
7 |
18 |
2 |
-5 |
4 |
-3 |
4 |
19 |
3 |
4 |
2 |
1 |
8 |
20 |
1 |
-4 |
7 |
2 |
2 |
21 |
1 |
3 |
3 |
5 |
6 |
22 |
3 |
1 |
5 |
-3 |
4 |
23 |
3 |
5 |
4 |
-4 |
4 |
24 |
2 |
3 |
5 |
6 |
10 |
25 |
2 |
3 |
3 |
4 |
6 |
26 |
1 |
4 |
5 |
3 |
7 |
27 |
1 |
1 |
4 |
-1 |
4 |
28 |
2 |
2 |
3 |
1 |
6 |
29 |
3 |
4 |
7 |
3 |
11 |
30 |
1 |
1 |
5 |
3 |
8 |
