
- •3Методические указания и требования
- •Выполнение заданий Первое задание. Построение графика функции.
- •Второе задание. Решение системы линейных уравнений.
- •4Решение методом обратной матрицы
- •5Решение по правилу Крамера.
- •6Решение методом Гаусса.
- •Третье задание. Работа с финансовыми функциями.
- •6.1Функция плт.
- •6.2Функция чпс.
- •6.3Функция пс.
- •Четвертое задание. Линейная оптимизационная задача.
- •Пятое задание. Сортировка и фильтрация данных.
- •Учебная информация
- •Варианты курсовых работ
- •Список литературы.
6Решение методом Гаусса.
Метод Гаусса основан на приведении матрицы системы к треугольному виду посредством последовательного исключения неизвестных из уравнений системы.
Расположите на листе матрицу коэффициентов и столбец правых частей, в диапазоне ячеек A1:D3. Скопируйте содержимое ячеек A1:D1 в ячейки A5:D5 и A9:D9. выделите диапазон A6:D6 и введите формулу =A2:D2-$A$1:$D$1*(A2/$A$1) и нажмите Ctrl+Shift+Enter. Методом автозаполнения скопируйте формулу из диапазона A6:D6 в диапазон A7:D7. Скопируйте значения ячеек A6:D6 в ячейки A10:D10 (для этого поместите в буфер обмена содержимое A6:D6, выделите диапазон в который надо скопировать выделенный диапазон и дайте команду Правка/ Специальная вставка и в появившемся окне поставьте переключатель в положение Значения). Далее выделите диапазон A11:D11, введите формулу { =A7:D7-$A$6:$D$6*(B7/$B$6)} и нажмите Ctrl+Shift+Enter. Прямая прогонка методом Гаусса завершена. Проведите обратную прогонку вводом в диапазоны A15:D15, A14:D14 и A13:D13 формул:
{ =A11:D11/C11}
{ =(A10:D10-A15:D15*C10)/B10}
{ =(A9:D9-A15:D15*C9-A14:D14*B9)/A9}
В диапазоне D13:D15 получено решение системы.
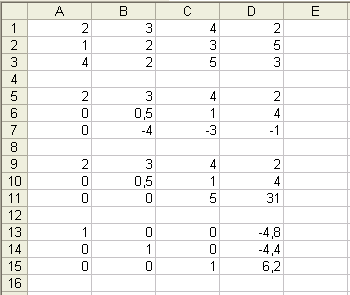
Проверка решения
Правильность вычислений проверьте умножением столбца решений на матрицу коэффициентов.
Третье задание. Работа с финансовыми функциями.
6.1Функция плт.
Постановка.
Вычислить30-годичную ипотечную ссуду со ставкой 8% годовых при начальном взносе 20% и ежемесячной (ежегодной) выплате
Реализация.
Для приведенного на рис 3.1. ипотечного расчета в ячейки введены формулы, показанные на рисунке 3.2.
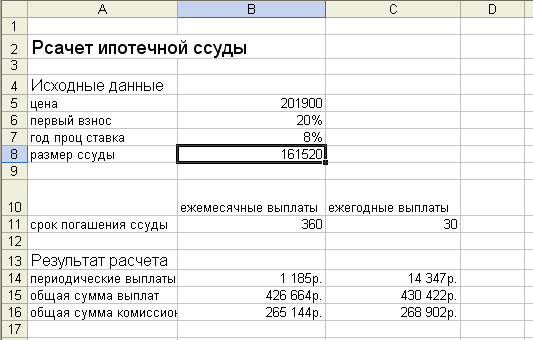
рис3.1. Расчет ипотечной ссуды.
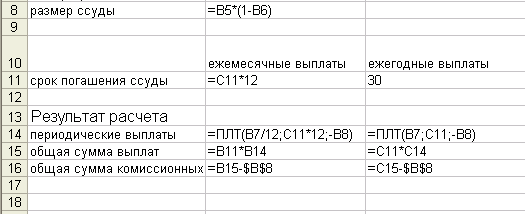
рис 3.2 Формулы для расчета ипотечной ссуды
Функция ПЛТ возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
Синтаксис
ПЛТ(ставка;кпер;пс;бс;тип)
ставка (i) процентная ставка по ссуде.
кпер (n) общее число выплат по ссуде.
пс (p) приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
бс требуемое значение будущей стоимости, или остатка средств после последней выплаты. если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0.
тип число 0 (нуль) или 1, обозначающее, когда должна производиться выплата (если тип равен 0 или опущен, то оплата производится в конце периода, если 1 – то в начале периода)
Если бс=0 и тип=0, то функция ПЛТ
вычисляет по формуле:
![]() ,
,
Для расчета ежемесячных выплат по 30-годичному займу из расчета 8% годовых аргумент ставка равен 8%/12 =0.08/12
аргумент кепер равен 30*12 n=30*12
Для расчета ежегодных выплат по 30-годичному займу из расчета 8% годовых
i=8% n=30
Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат умножьте возвращаемое функцией ПЛТ на величину кепер (n).
В функциях, связанных с интервалами выплат, выплачиваемые вами деньги (такие как депозит на накопление) представляются отрицательным числом, а деньги, которые вы получаете (чеки, дивиденды) предоставляются отрицательным числом, поэтому третий параметр функции ПЛТ берется с отрицательным значением.
