1.2.7. Двоточкова перспективна проекція

Якщо два елементи в четвертому стовпці матриці перетворення ненульові, то маємо двоточкову або кутову, перспективу. У разі двоточкової перспективи є дві точки збіжності на відповідні осі. При отримаємо дві точки збіжності – на осі ОХ і осі ОY. По осі ОZ відбувається паралельне проектування, де нормалізований вектор має вигляд

Зміною можна регулювати VP1, VP2 точки збіжності на осі OX (x= ) і на осі OY (y= ). На рис. 1.20,а зображена двоточкова перспективна проекція одиничного куба на площину z = 0 при . Тут координати вузлів фронтальної і задньої частини куба збігаються, тому проекція інформаційна. Іншого типу проекцію (див. рис.1.20б) отримаємо, якщо попередньо відцентруємо вісь z щодо фронтальної площини.

а б

Рис. 1.20. Двоточкова перспективна проекція

Двоточкова перспектива матиме точки сходження на осях OX і OZ у разі ненульових першого і третього коефіцієнтів останнього стовпця матриці перетворень , а на осях OY і OZ – при .

Для того, щоб отримати інформаційну двоточкову перспективу, треба спочатку повернути зображення відносно осі y на деякий кут і змістити на деяку точку (0, , ,1). Точка спостереження повинна бути на осі z на заданій відстані, а проектування – відбуватись на площину z=0.

= (1.19)

Унаслідок таких перетворень отримано двоточкову перспективну проекцію. Тут ненульовими є перший і третій коефіцієнти четвертого стовпця матриці перетворень, На рис. 1.21 зображена проекція одиничного куба на площину z = 0, отримана за допомогою перетворень (1.19), що є результатом обертання навколо деякої осі та перенесенням на деяку точку.

Лінії, які спочатку були паралельні до осей OX, перетинаються в першій точці збіжності VP1 (бо ), а ті, які були паралельні осі OZ – у другій VP2 ( ). Лінії, які були паралельні до осі OY, залишились паралельними ( ).

Рис. 1.21. Двоточкова перспективна проекція

1.2.8. Триточкова перспективна проекція

У разі перших трьох ненульових елементів у четвертому стовпці матриці отримаємо триточкову або косу перспективу з трьома точками збіжності, відповіднО на осях ОХ, ОY і ОZ.

На рис. 1.22 зображена триточкова перспективна проекція одиничного куба на площину z = 0 при

а б

Рис. 1.22. Триточкова перспективна проекція

Інформаційну триточкову перспективу, як і у випадку двоточкової перспективи, з точкою спостереження на осі z, можна отримати шляхом обертання навколо двох різних осей. Тут треба спочатку повернути зображення відносно осі y на деякий кут , А потім навколо осі х на кут і змістити на точку ( , , ,1). Точка спостереження повинна бути розташована на заданій відстані, а проектування – відбуватись на площину z=0.

Результатом є ненульові перші три коефіцієнти четвертого стовпця матриці перетворень, які й визначають перспективу. На рис. 1.22 зображена проекція одиничного куба на площину z=0 за допомогою перетворень (1.20). Зазначимо, що лінії, які спочатку були паралельні до осей OX OY і OZ, перетинаються в кожній з трьох точок збіжності VP1,VP2 і VP3

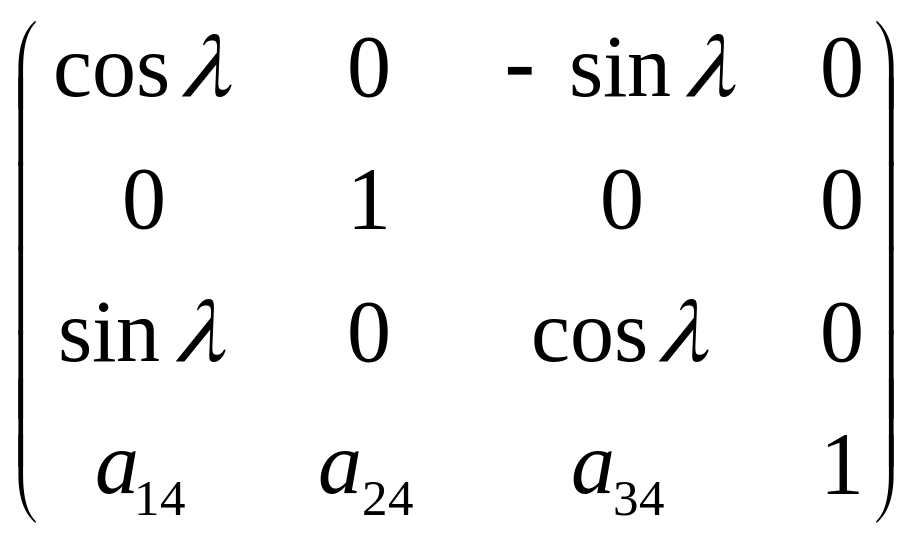х х = (1.20)