Деталізовані плани практичних занять з „математики для економістів”

для спеціальностей „Економіка підприємства”, специ,

I курс, I семестр, 2014 н.Р. Практичне заняття №1 елементи теорії матриць. Визначники.

Теоретичні запитання:

1. Що називається матрицею?

2. Які є різні типи матриць?

3. Як визначаються: сума двох матриць, добуток двох матриць на число, різниця двох матриць?

4. Які матриці називаються узгодженими? Як визначається добуток двох матриць?

5. Які перетворення матриці називаються елементарними?

6. Що називають рангом матриці? Як знаходиться ранг матриці?

Розв’язати вправи:

1. Знайти та з рівняння .

2. Обчислити лінійну комбінацію матриць:

а) 2А-4В, якщо , .

3. Два залізобетонних заводи випускають вироби M, N, P вищої, першої та другої якості. Кількість випущених кожним заводом виробів за кожною категорією якості характеризується наступною таблицею:

Категорія якості	Готові вироби
	I завод			II завод
	M	N	P	M	N	P
Вища	150	240	320	280	300	450
Перша	100	130	175	150	150	170
Друга	25	15	20	30	20	18

Який загальний випуск виробів за означеними категоріями якості?

4. Підприємство випускає продукцію двох видів, використовуючи при цьому сировину трьох типів. Витрати сировини на виробництво продукції задаються матрицею , де – кількість одиниць сировини і-го типу, що використовується на виготовлення одиниці продукції j-го виду. План щоденного випуску продукції передбачає 90 одиниць продукції першого виду і 120 одиниць продукції другого виду. Вартість одиниці кожного типу сировини відповідно дорівнює 8, 5 і 10 гр. од. визначити загальні витрати сировини , необхідної для щоденного випуску продукції, а також загальну вартість цієї сировини.

5. Визначити ранг матриці .

Теоретичні запитання:

7. Що називають визначником другого порядку?

8. Що називається визначником третього порядку?

9. Сформулюйте основні властивості визначників.

10. Що називається мінором та алгебраїчним доповненням?

11. Як обчислюються визначники вищих порядків?

12. Яка матриця називається оберненою?

13. Як визначається обернена матриця до заданої?

Розв’язати вправи:

1. Записати та обчислити всі мінори другого порядку матриці:

а) , б) .

2. Обчислити визначники:

а) , б) , в) .

Домашнє завдання:

1. Обчислити:

а) 7А+2В-3С, якщо , , .

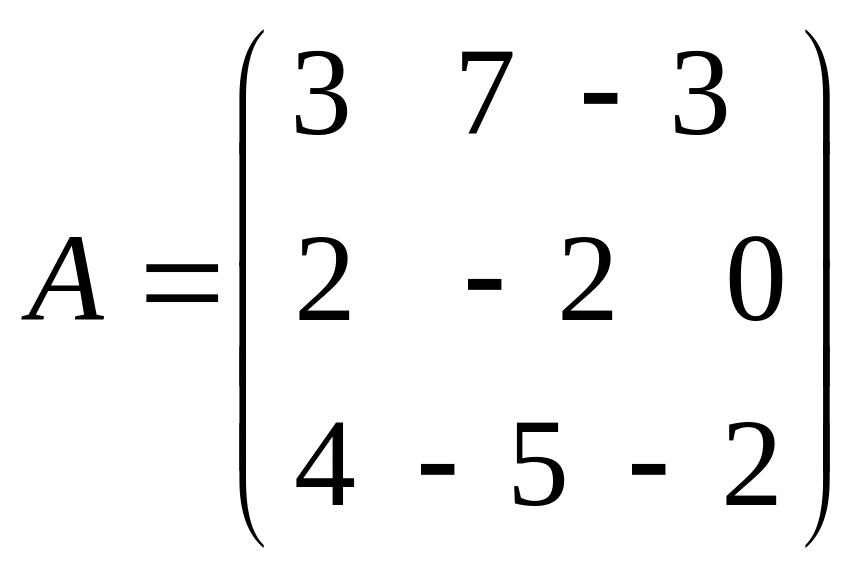б) .

2. Обчислити визначники:

а) , б) , в) .

Практичне заняття №2 системи лінійних рівнянь

Теоретичні запитання:

1. Що називається системою лінійних рівнянь з невідомими?

2. Яка система лінійних рівнянь називається сумісною, несумісною, визначено, невизначеною?

3. Сформулюйте теорему Крамера

4. У чому полягає метод Гаусса?

5. У чому полягає матричний метод розв’язування системи лінійних рівнянь?

6. Сформулюйте теорему Кронекера-Капеллі

Розв’язати вправи:

1. З деякого листового матеріалу необхідно викроїти 200 заготовок типу А, 260 – типу В, і 290 – типу С. При цьому можна застосувати три способи розкроювання. Кількість заготовок, одержуваних з кожного листа при кожному способові розкроювання, наведена в наступній таблиці.

Тип заготовки	Спосіб розкроювання
	1	2	3
А	3	2	1
В	1	6	2
С	4	1	5

Записати в матричній формі умови виконання завдання. Встановити, скільки листів буде потрібно для викроювання означеної кількості заготовок. Систему рівнянь розв’язати двома способами (методом Крамера, методом Гаусса).

2. Двома способами (методом Крамера, методом Гаусса) розв’язати системи рівнянь:

а) б)

Домашнє завдання:

1. Двома способами (методом Крамера, методом Гаусса) розв’язати системи рівнянь:

а) б)