Тема 4. Теплофізичні характеристики (параметри) вологих матеріалів

Лекція 7. Основні теплофізичні параметри вологих матеріалів

1. Теплоємність

2. Коефіцієнт теплопровідності

3. Коефіцієнт температуропровідності

1. Повна інформація про вологі матеріали передбачає знання не тільки їх теплофізичних характеристик і параметрів (теплоємність С, коефіцієнти теплопровідності і термопровідності ), але й такі, як кількість теплоти, яка виділяється чи споживається при фізико–хімічних процесах, а також параметри і функції стану системи (тиск, об’єм, температура, ентальпія і інше).

Вивчення вказаних характеристик і параметрів у взаємозв’язку є важливими даними для науково-технічних завдань збереження сільськогосподарської продукції.

Питома теплоємність вологого матеріалу (вимірюється в Дж/кг·к) розраховується як середньозважувана величина між теплоємністю сухої речовини С_с.реч. і теплоємністю води С_в, яка приймається рівною 4,19 кДж/кг∙К:

(4.1)

або (4.2)

Теплоємність сухої речовини різних матеріалів становить 1257-1676 Дж/кг · к або 0,3-0,4 ккал/(кг ⁰С).

Якщо теплоємність вологого матеріалу віднести до кілограма сухої речовини, то отримаємо теплоємність в Дж/ (кг с.реч. ·К):

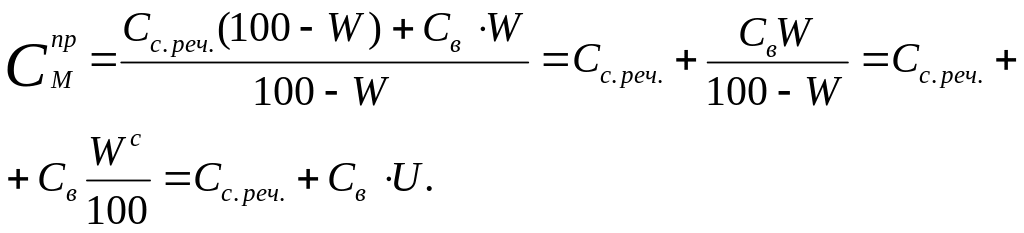(4.3)

Згідно з формулами, залежність між теплоємністю матеріалу і його вологістю має лінійний характер. Але при проведенні спеціальних досліджень було встановлено, що на прямих існують переломні точки для деяких матеріалів.

Появу таких переломних точок на графіках С_м = f(W) пояснюється двома причинами:

– фізико-хімічними змінами сухої речовини матеріалу в різних інтервалах вологості;

– впливом таких факторів, як пористість матеріалу, наявність повітря у твердому скелеті, співвідношення між водою, яка знаходиться в рідкому і пароподібному стані та інше.

Але вплив вказаних факторів на теплоємність матеріалу є незначним. Суттєвий вплив вони мають лише на теплопровідність вологого матеріалу. Велике значення для теплоємності можуть мати внутрішні процеси, які відбуваються у разі зволоження чи сушіння матеріалу.

2. Перенесення тепла у вологих матеріалах суттєво відрізняється від передачі тепла в сухих матеріалах:

а) волога впливає на теплопровідність твердого скелета пористого тіла, в порах якого вона знаходиться;

б) перенесення тепла тісно пов’язане з безпосереднім перенесенням вологи в середині матеріалу.

Тепло може передаватись також конвенцією через пори, в яких знаходиться газ і рідина та випромінюванням між стінками пор. Тому розрізняють істинний і еквівалентний коефіцієнти теплопровідності.

Істинний коефіцієнт теплопровідності є коефіцієнтом пропорційності в рівнянні Фур’є

(4.4)

де q – щільність потоку тепла в твердому ізотропному тілі, Вт/м²

- градієнт температури, К/м.

Еквівалентний, або ефективний коефіцієнт теплопровідності λ_екв. характеризує здатність вологого матеріалу проводити тепло вищевказаними способами:

(4.5)

де – коефіцієнт теплопровідності твердого скелета матеріалу;

– коефіцієнт кондукції (теплопровідності) рідини і пароповітряної суміші, які перебувають у стаціонарному стані в порах матеріалу;

– коефіцієнт, який характеризує перенесення тепла конвенцією повітря всередині матеріалу;

– коефіцієнт, який характеризує перенесення тепла за рахунок перенесення маси води всередині матеріалу (у вигляді рідини та у вигляді пари);

– коефіцієнт променевої теплопровідності.

З врахуванням останнього виразу

(4.6)

Встановлено, що при діаметрі пор менше 0,5 мм променевим теплообміном можна нехтувати, а при діаметрах пор менших 5 мм і ∆θ≈ - також конвективним теплообміном.

Для пористих матеріалів інтерес становить залежність коефіцієнта від двох взаємопов’язаних факторів – діаметра пори d i пористості матеріалу або його щільності . Чим вище щільність матеріалу, тим більше Відповідно чим більший розмір частин, який утворює скелет зернового матеріалу, тим більше

Вплив форми частин у двохфазній системі (дисперсний матеріал – повітря) на коефіцієнт теплопровідності знаходять відображення у формулі, отриманій за принципом електротеплової аналогії (теорії Максвела – Бургера – Еймена):

(4.7)

де - коефіцієнт теплопровідності і об’єми твердої і газової фаз.

Коефіцієнт ψ залежить від форми частин.

Для кулькових зерен

(4.8)

Для зерен циліндричної форми

(4.9)

Для зерен у формі тонких пластин

(4.10)

Точність результатів, отриманих за вказаними формулами залежить від правильності вибраної моделі відповідно реальній структурі матеріалу.

а)

б)

в)

г)

д)

е)

є)

Рис. Моделі зернистого матеріалу:

• необмежені пластини, а-перпендикулярні; в-паралельні тепловому потоку;

• система брусків при П<50% (в) і П>50% (г);

• система кубів (д);

• тетраїдна рихла (е) і щільна (є).

Існують і інші формули визначення Крім цього, замість пористості в розрахункові формули вводять щільність (об’ємну масу) системи . Зв’язок між ними встановлюється через щільність твердої фази _тв:

(4.11)

Вплив вологості матеріалу W на обумовлена ступенем дисперсності матеріалу (крупно-, середньо-, дрібнодисперсні). У межах малої вологості матеріалу ріст відображається лінійно, причому швидкість зростання тим більше, чим крупність частинки зерен.

При великій вологості матеріалу ріст поступово, призупиняється (для крупнозернистих), залишається лінійним (для середньозернистих) і різко зростає (для дрібнозернистих).

П

Рис. 4.1. Рідинна манжета (стикова рідина) між двома сферичними частинами

риймається, що спочатку (при малій вологості матеріалу) волога заповнює дрібні пори між зернами, після цього насичена волога переходить у повітряні пори і накопичується в основному в місцях стику зерен. Таким чином, при малій вологості система в основному складається у повітряних пор і твердого скелета; при великій вологості волога заповнює весь міжзерновий простір і повністю насичує їх.

К

α

ористуючись модельним тілом, можна розглянути поведінку капілярної рідини при різному заповненні пор. В точці контакту частин в міру надходження рідини утворюється накопичення рідини, яка має форму подвійної ввігнутої лінзи.

α

α

Середня кривизна такої поверхні рівна при r₂<r₁. Радіуси кривизни при певному змочуванні залежать від радіуса частин R і кута α. Таке накопичення рідини називають рідинною манжетою, а рідину – стиковою.

Капілярний тиск стикової рідини буде рівний

, (4.12)

де К – деяка постійна, яка залежить тільки від кута α. Якщо рідини мало, то вона розподілена дискретними розділеними кільцями. Якщо розміри частин незначні, то із збільшення надходження рідини манжети поступово збільшуються і зливаються між собою. Таке злиття відбувається при куті α=30⁰.

б)

а)

α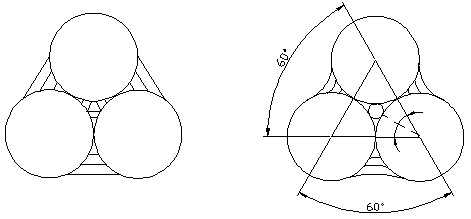

Рис. 4.2. Перехід від стикового стану до канатного; а - защемлена вода, б – защемлене повітря

К

а)

анатним станом рідини називається такий стан, коли рідка плівка неперервно розміщена навколо тіла. Капілярний стан відрізняється від канатного наявністю хоча б однієї вільної поверхні для утворення меніска капіляра.

3. Коефіцієнт температуропровідності а є важливою характеристикою матеріалу, який визначає його теплоінерційні властивості; чим вище а, тим швидше відбувається нагрівання і охолодження матеріалу. Тому коефіцієнт а необхідно враховувати при дослідженні і розрахунку нестаціонарних процесів – нагрівання, охолодження, сушіння, зволоження та інших.

, (4.13)

де - коефіцієнт теплопровідності матеріалу;

С – питома теплоємність;

- щільність (об’ємна маса).

Добуток - це теплоємність одиниці об’єму матеріалу. Вона характеризує теплоакумулюючу здатність; чим більше , тим при такому ж значенні λ, коефіцієнт а буде меншим.

Аналогічно еквівалентному коефіцієнту теплопровідності матеріалу можна ввести еквівалентний коефіцієнт температуропровідності а_екв. Тоді диференційне рівняння внутрішнього тепла буде мати вигляд:

(4.14)

Загалом характер зміни параметрів тіла в процесі теплового зневоднення матеріалом розглядає кінетика процесу.

Під кінетикою процесу розуміють зміну середнього вологовмісту і середньої температури тіла .

Знаходження полів вологовмісту U = (X, Y, Z, δ) пов’язано із рішенням диференційних рівнянь масо- і теплоперенесення за відповідних граничних умов. Ця система є системою нелінійних диференціальних рівнянь, тому їх вирішують з допомогою ЕОМ.

Лекція 8. Параметри сушильного агенту

1. Діаграма Id вологого повітря (газу)

2. Визначення параметрів агента сушіння

1. Газоподібний теплоносій (суміш повітря з топковими газами, холодне або підігріте повітря), за допомогою якого матеріал нагрівається для випаровування з нього вологи, називається сушильним агентом або агентом сушіння.

Важливими параметрами повітря й агента сушіння є температура t, відносна вологість φ, вологовміст d і ентальпія (тепловміст) I. Температура вимірюється в градусах Цельсія або Кельвіна. Відносною вологістю φ називають відношення маси водяної пари в 1 м³ вологого повітря або агента сушіння (г/м³) до максимально можливої маси водяної пари в 1 м³ цього ж вологого повітря або агента сушіння (г/м³) при одній і тій самій температурі й барометричному тиску; вологість φ може вимірюватись у відносних величинах або відсотках. Вологовмістом d називається маса водяної пари в грамах (г), що міститься у вологому повітрі або агенті сушіння, віднесена до1 кг сухого повітря або агента сушіння; вимірюється вологовміст d в грамах на кілограм (г/кг СП) (тут СП означає сухе повітря або газ). Ентальпія (тепловміст) I є теплофізичною характеристикою стану газу й дорівнює сумі внутрішньої енергії й добутку тиску на об’єм. Для процесів, що проходять при сталому тиску, якими можна вважати процеси при сушінні, приріст ентальпії дорівнює кількості теплоти, що надається системі. Вимірюється ентальпія відношенням енергії (теплоти) до 1 кг сухого повітря (газу), тобто кДж/кг СП. Між параметрами t, φ, d та I існує зв'язок, який графічно зображений на I-d діаграмі – (рис. 4.3).

Враховуючи, що вологе повітря є основним об'єктом вентиляційного процесу, в області вентиляції доводиться часто визначати ті або інші параметри повітря. Щоб уникнути численних обчислень, їх визначають зазвичай за Id діаграмою. Вона дозволяє швидко визначити всі параметри повітря за двома відомими. Використання діаграми дозволяє уникнути обчислень за формулами і наочно відобразити вентиляційний процес. Аналогом Id діаграми на заході є діаграма Молье або психрометрична діаграма.

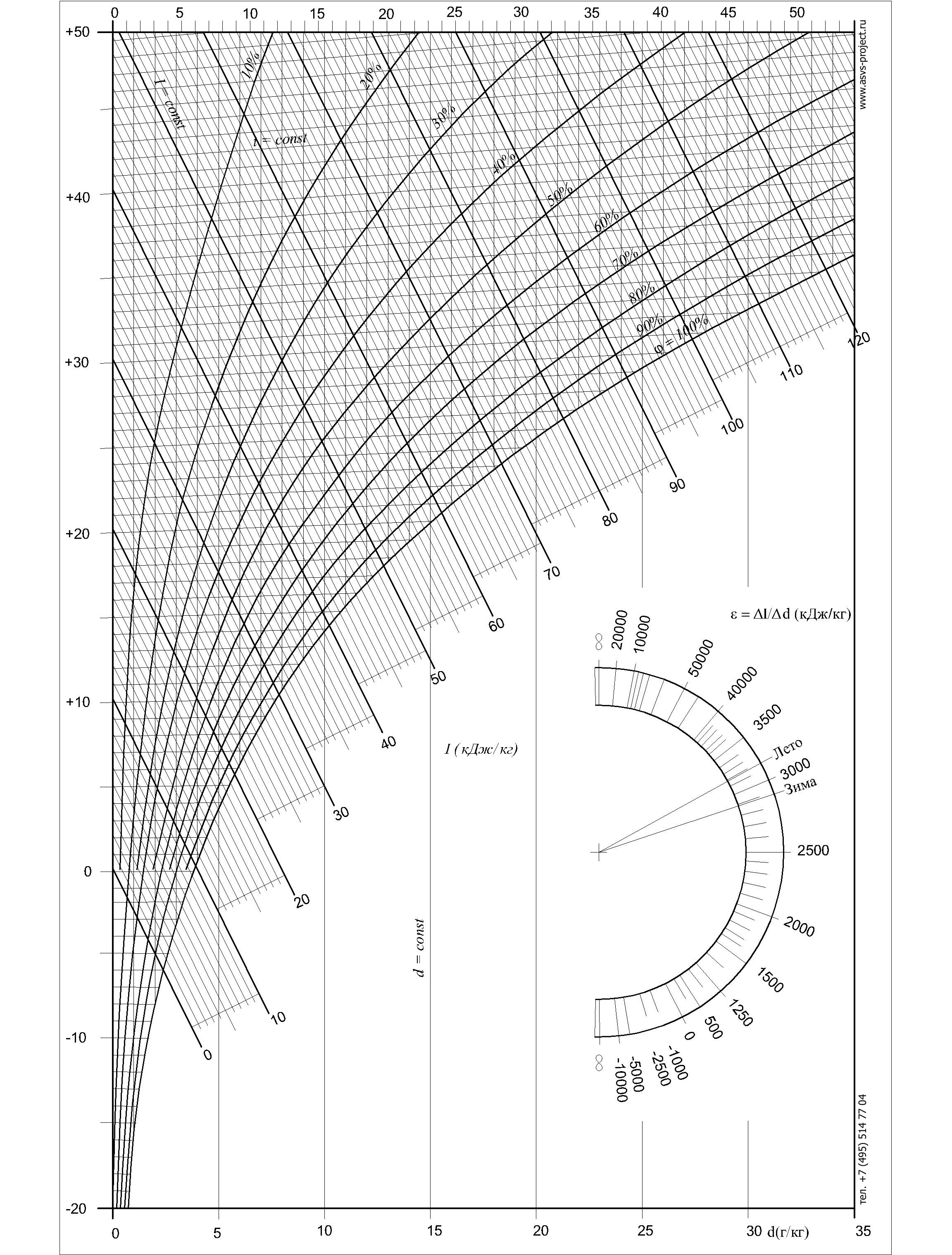
Рис. 4.3 Загальний вигляд I-d діаграми вологого повітря

Оформлення діаграми в принципі може бути кілька різних. Типова загальна схема Id діаграми показана на рис. 4.3. Діаграма представляє з себе робоче поле в косокутної системі координат Id, на якому нанесено декілька координатних сіток і по периметру діаграми - допоміжні шкали. Шкала вологовмісту звичайно розташовується по нижній кромці діаграми, при цьому лінії постійних вологовмісту представляють вертикальні прямі. Лінії постійних ентальпій представляють паралельні прямі, звичайно йдуть під кутом 135 ° до вертикальних лініях вологовмісту (у принципі, кути між лініями ентальпії і вмісту вологи може бути й іншим). Косокутна система координат обрана для того, щоб збільшити робоче поле діаграми. У такій системі координат лінії постійних температур представляють із себе прямі лінії, які йдуть під невеликим нахилом до горизонталі і злегка розходяться віялом.

Робоче поле діаграми обмежене кривими лініями рівних відносним вологостям 0% і 100%, між якими нанесені лінії інших значень рівним відносним вологостям з кроком 10%.

Шкала температур зазвичай розташовується по лівій кромці робочого поля діаграми. Значення ентальпій повітря нанесені зазвичай під кривою Ф = 100. Значення парціальних тисків іноді наносять по верхній кромці робочого поля, іноді по нижній кромці під шкалою вологовмісту, іноді по правій кромці. В останньому випадку на діаграмі додатково будують допоміжну криву парціальних тисків.

Діаграма будується для визначення барометричного тиску (99,3 кПа). По горизонтальній осі вологовміст d, по осі ординат – ентальпія I, а віссю абсцис служить лінія, розміщена під кутом 135^° до осі ординат у бік осі d.

На діаграмі показані графічні залежності I від d при різних температурах t і вологостях φ . Точки на діаграмі, що відповідають одній і тій самій температурі й одній і тій самій вологості, об’єднуються у спільні лінії. На діаграмі також об’єднуються в лінії точки, що характеризуються однією і тією самою ентальпією і одним і тим самим вологовмістом. Через особливості побудови осі абсцис діаграми лінії на ній, що характеризуються одним і тим самим I (тобто тим, що I=const) , розміщені під кутом 135^° до осі ординат паралельно осі абсцис, а лінії, які характеризуються тим , що d=const, вертикальні, тобто паралельні осі ординат. Лінії, які характеризуються тим, що t=const (ізотерми),мають деякий нахил, що збільшується з ростом I. Лінії , які характеризуються тим , що φ=const, мають вид пучка, поки повітря матиме температуру , при якій тиск пари дорівнює барометричному тиску. При більшій температурі лінії φ=const зображаються прямими лініями, майже паралельними осі ординат. Чим вища лінія φ=const, тим менше φ. Можливість розв’язання забезпечується, якщо з чотирьох параметрів t, φ, d та I задані щонайменше два.

2. Для відображення процесу визначення параметрів вологого повітря на Id діаграмі, можна показати лише основні лінії, та характерні точки. Точка А на діаграмі відображає певний стан повітря, а лінія - процес зміни його стану. Визначення параметрів повітря, що має певний стан, що відображається точкою А, показано на рис. 4.4

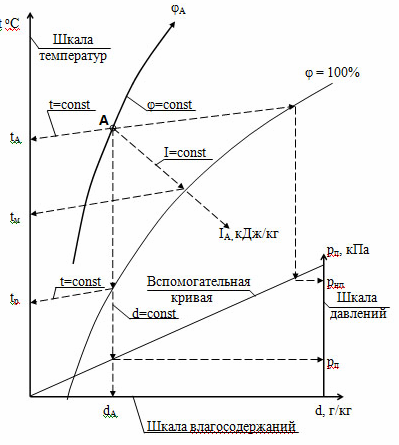
Рис.4.4 Визначення параметрів вологого повітря

Агент сушіння утворюється в топці або калорифері. На рис.4.5 зображена схема топки (калорифера) й надходження до неї повітря з параметрами tₒ, φₒ , dₒ, Iₒ і вихід з неї агента сушіння з параметрами t₁ , φ₁, d_1, I_1.Фізичний зміст цих параметрів розкритий вище. Параметри t₁ , φ₁, d_1, I_1. змінилися завдяки тому , що в топці (калорифері) при спалюванні палива виділилося Q теплоти. Температура t₁ задана: це температура агента сушіння, вона не повинна бути більшою за допустиму. Визначимо, чому рівні параметри φ₁, d_1, I₁ залежно від tₒ, φₒ , dₒ, Iₒ, t₁ та Q.

Рис. 4.5 Схема до розрахунку параметрів агента сушіння

Кількість виділеної теплоти

Q= m_n q_n η_т , (4.15)

де m_n − маса палива, що йде на сушіння, кг/год; q_n− теплота спалювання палива, кДж/кг; η_т− ККД топки, що приймається таким, що дорівнює 0,85…0,95.

Вказано, що для процесів сушіння приріст ентальпії дорівнює кількості теплоти, яка надана системі. Тому

Q=L(I₁- I₀ ), (4.16)

де L − маса сухого агента сушіння, що подається за одиницю часу, кг/год.

Вологовміст d₁ = d₀, якщо підігрівання повітря проводиться за допомогою калорифера. Якщо ж підігрів проводиться за допомогою топки шляхом змішування повітря з топковими газами, то вологовміст d₁ > d₀ за рахунок згоряння водню й вологи, що міститься у паливі.

Знаючи t₁ і d₁, можна легко визначити I₁ та φ₁ за діаграмою I-d. Розв’язання таких задач показано на рис. 4.6, де також зазначено, як змінюється на діаграмі положення точки, що характеризує параметри повітря при нагріванні у калорифері. У зовнішнього повітря з параметрами φ₀ та d₀ (точка А), внаслідок нагрівання в калорифері при d=const , температура підвищується від t₀ до t; тоді ентальпія стає I₁ замість I₀ (точка В ), а вологість повітря зменшується при цьому від φ₀ до φ₁. Як видно з рис. 4.6, зміна параметрів повітря (агента сушіння) у даному випадку проходить по вертикальній лінії АВ.

Рис. 4.6 Зміна параметрів повітря (агента сушіння ) при нагріванні

При нагріванні повітря за допомогою топки внаслідок збільшення вологовмісту d від d₀ до d₁^ʹ і температури від t₀ до t₁^ʹ (позначення d₁^ʹ та t₁^ʹ прийняті для нагрівання за допомогою топки замість d₁ та t₁ ), зміна параметрів повітря буде відбуватися по похилій лінії АВ′. Ця побудова на рис. 4.6 показана за умови, що I₁ однакове при нагріванні повітря і калорифером, і за допомогою топки, що можливо, якщо і Q і L одні й ті самі (і калорифера і топки). Положення точки В' також, як і положення точки В , дозволяє визначити ентальпію I₁ та параметр φ агента сушіння (підігрітого повітря) , який стосовно точки В' позначений φ^ʹ₁.Оскільки ентальпія точки В' така сама, як і точки В , то її позначення залишилось I₁. Знаючи I₁, I₀ , m_n q_n η_т тобто Q, можна з 4.16, враховуючи 4.15, визначити необхідну витрату сухого агента сушіння, (точніше масу сухого агента сушіння, що подається за одиницю часу):

L= m_n q_n η_т /(I₁- I₀). (4.17)

Необхідне підведення теплоти Q для отримання агента сушіння з параметрами t₁ , φ₁, d_1, I₁ і визначається за рис. 4.6, якщо відома величина L.

З представлених даних видно, що можна досягнути одного й того самого значення I₁ при сталому I₀ , якщо збільшити Q, але зменшити L, або збільшити L, але зменшити Q.