- •Аэрогидрогазодинамика. Учебное пособие для практических занятий
- •Isbn 5-696-00000-0 © Издательство юУрГу, 2014
- •Предисловие
- •Часть 1. Теоретические предпосылки и условия задач Тема 1. Аэродинамические силы и коэффициенты
- •Характерные размеры ла
- •Тема 2. Уравнения: неразрывности, импульса, Бернулли
- •Тема 3. Изэнтропические течения
- •Связь параметров торможения с числом м движущегося газа
- •Связь критических параметров с параметрами торможения
- •Тема 4. Скачки уплотнения
- •4.1. Прямые скачки уплотнения
- •4.2. Косые скачки
- •Тема 5. Сверхзвуковое обтекание тел вращения
- •5.1. Обтекание конуса сверхзвуковым потоком
- •5.2. Обтекание тел вращения с криволинейной образующей ( )
- •Давление в донной части
- •Аэродинамические коэффициенты для тел вращения
- •Тема 6. Гидростатика Основное уравнение гидростатики
- •Относительный покой
- •Силы давления жидкости на криволинейные поверхности
- •Тема 7. Критерии подобия
- •Тема 8. Путевые потери напора Течение вязкой жидкости по трубам
- •Уравнение Бернулли с учетом потерь давления на трение
- •Тема 9. Местные сопротивления. Истечения через отверстия и насадки
- •Истечение через диафрагму
- •Истечения через отверстия и насадки при постоянном напоре
- •Тема 10. Нестационарные течения
- •10.1 Неустановившиеся течения
- •10.2. Гидравлический удар в трубах
- •Часть 2. Решения задач Тема1. Аэродинамические силы и коэффициенты
- •Тема 2. Уравнения неразрывности, импульса, Бернулли
- •Тема 3. Изэнтропические течения
- •Тема 4.Скачки уплотнения
- •Тема 5.Обтекание тел
- •Тема 6. Гидростатика
- •Тема 7. Критерии подобия
- •Тема 8. Путевые и местные потери напора
- •Тема 9. Истечения через отверстия и насадки при постоянном напоре
- •Тема 10. Нестационарные течения
- •10.1 Неустановившиеся течения
- •10.2. Гидравлический удар в трубах
- •Приложения приложение №1. Параметры воздуха.
- •Приложение №2. Физические свойства газов.
- •Плотность некоторых газов при 00 и 760 мм.Рт.Ст.
- •Зависимость показателя адиабаты для воздуха от температуры
- •Приложение №3. Международная система единиц (си)
- •Библиографический список
Тема 6. Гидростатика Основное уравнение гидростатики
Проецируя уравнение
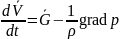
(6.1)
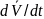 = 0, затем, умножая каждое уравнение на
дифференциал соответствующей оси, после
суммирования уравнений получаем:
= 0, затем, умножая каждое уравнение на
дифференциал соответствующей оси, после
суммирования уравнений получаем:

– основное уравнение гидростатики.
Относительный покой
0
y
α
β<0
x
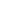








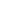
 =?
=?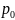

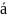
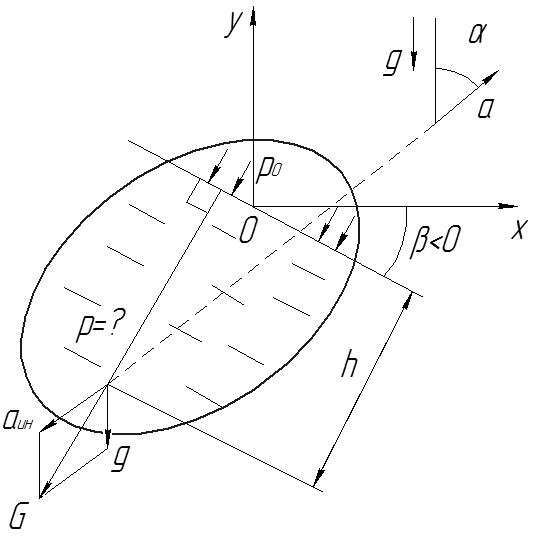 усть
жидкость (оставаясь в покое относительно
сосуда) движется вместе с ним с ускорением
усть
жидкость (оставаясь в покое относительно
сосуда) движется вместе с ним с ускорением
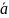 ,
направленным под углом α к
вертикальной оси у (рис.6.1). Тогда
свободная поверхность жидкости будет
располагаться под углом
,
направленным под углом α к
вертикальной оси у (рис.6.1). Тогда
свободная поверхность жидкости будет
располагаться под углом
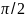 к вектору
к вектору
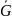 (единичной массовой силы, включающей
инерционную, даламберову силу),
модуль которого определится по теореме
косинусов выражением
(единичной массовой силы, включающей
инерционную, даламберову силу),
модуль которого определится по теореме
косинусов выражением
h

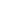
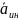
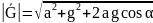 . (6.2)
. (6.2)



Рис. 6.1. Схема действия сил
и ускорений
Проекции единичной массовой силы на оси координат х, у будут иметь вид
(6.3)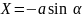 ,
,
 .
.
(6.4)
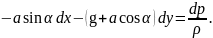
(6.5)
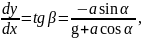
из которого определится угол β отклонения свободной поверхности от горизонтального положения.
Давление
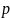 определится интегрированием
уравнения (6.4) от p0
на поверхности жидкости при x
= y = 0 до p
в точке с координатами x,
y выражением
определится интегрированием
уравнения (6.4) от p0
на поверхности жидкости при x
= y = 0 до p
в точке с координатами x,
y выражением
(6.6)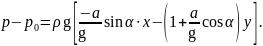
Более удобным часто бывает другое простое соотношение
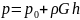 ,
,
где G – единичная массовая сила.
Силы давления жидкости на криволинейные поверхности
Сила давления на площадку dS
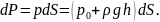 (6.8)
(6.8)
Проецируя ее на произвольное направление α (рис. 6.2), получаем
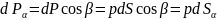 ,
(6.9)
,
(6.9)
где
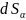 – проекция площадки dS
на плоскость, перпендикулярную
направлению α. Или
– проекция площадки dS
на плоскость, перпендикулярную
направлению α. Или
 (6.10)
(6.10)
α



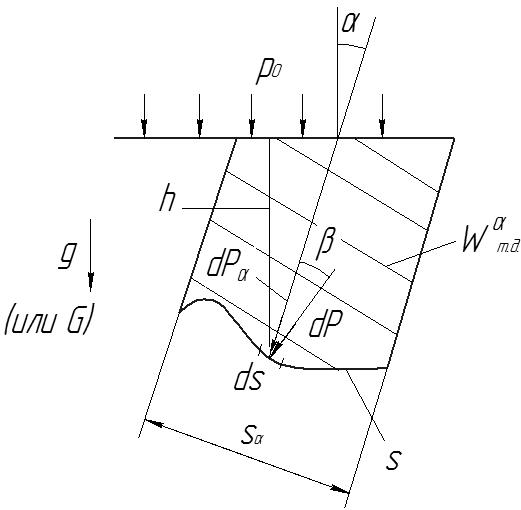 осле
интегрирования (6.10) получим
осле
интегрирования (6.10) получим
 , (6.11)
, (6.11)







h