Лекція №6 (Семестр 5. 2014/2015)
5. Теоретичні закони поширення коливань температури у ґрунті
Якщо ґрунт однорідний у вертикальному напрямку, то його температура Т на глибині z в момент часу t визначається із рівняння теплопровідності - рівняння в приватних похідних, яке описує поширення тепла в заданій області простору в часі (14)
(14)
Для рішення рівнянь щодо розподілу тепла в ґрунті допускаються деякі припущенні, а саме: коливання температури ґрунті повторюють коливання радіаційного балансу поверхні; коливання температури з глибиною припиняються на деякій глибині; температуропровідність грунту не змінюється з глубиною.
Тоді аналітичне рішення рівняння (14) має простий вигляд
(15)
де Т(z,t
)− температура на глибині z
у момент часу t; T0
середня температура поверхні за період;
A0
амплітуда температури поверхні; П
– період коливань;
– початкова фаза коливань,
– є
функція запізнення, яка описується
виразом
,
(16)
тобто обернено залежить
від температурнопроводності
,
та періоду коливань
.
З рівняння (15) випливають теоретичні закони поширення температурних коливань у ґрунті.
I. Закон незмінності періоду коливань з глибиною:
П = const. (17)
II. Закон експоненційного зменшення амплітуди коливань температури у ґрунті з глибиною
З рівняння (15) випливає, що амплітуда температурних коливань зменшується з глибиною в грунті експоненціально
(18)
З другого закону можно зробити такі висновки:
a) глибини z , на яких в різних ґрунтах (індекси 1 і 2) амплітуди температурних коливань одного періоду зменшуються в однакову кількість разів, відносяться між собою, як корні квадратні з величин температуропровідності цих ґрунтів
.
(19)
Рівняння
(19) показує, що ґрунти, які мають велику
температуропровідність
,
проводять тепло на більші глибини
,
особливо вологі ґрунти.
б) глибини, на яких в одному і тому ж ґрунті амплітуди коливань різних періодів (індекси 1 і 2) зменшуються в однакову кількість разів, відносяться між собою, як корні квадратні з величин періодів коливань
.
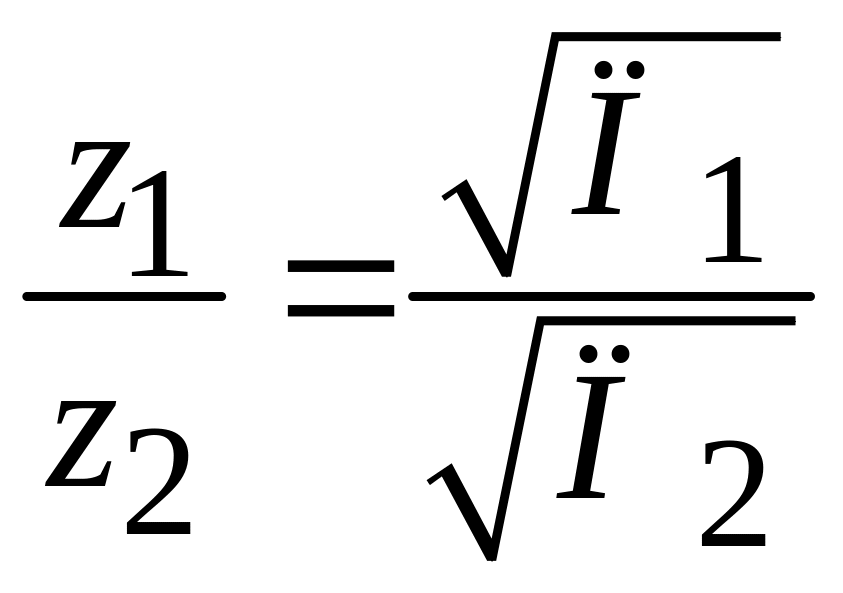(20)
Отже,
порівняння глибин проникнення коливань
добового періоду та річного показує,
що річні коливання при середніх умовах
проникають на глибини у 19 разів більші,
ніж добові коливання. Добові коливання
затухають на глибині біля 1м, а річні на
глибині біля 20 м., так як
III. Закон запізнення наступу екстремальних температур на глибинах порівняно з поверхнею.
З рівняння (15) запишемо умову наступу максимальної температури на поверхні
соs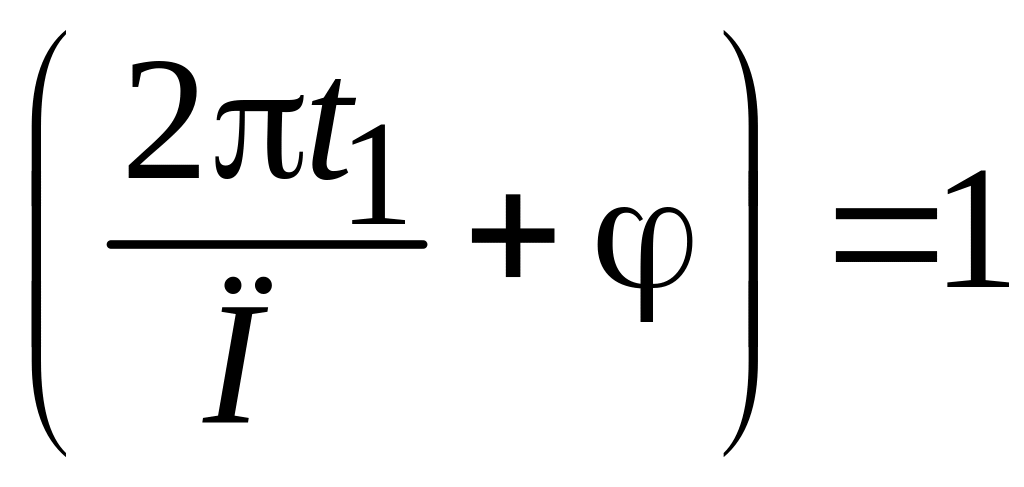
,
(21)
на глибині z
cos
.
(22)
Порівнюючи рівняння (21) і (22) отримаємо
t2
t1 =
.
(23)
З урахуванням рівняння
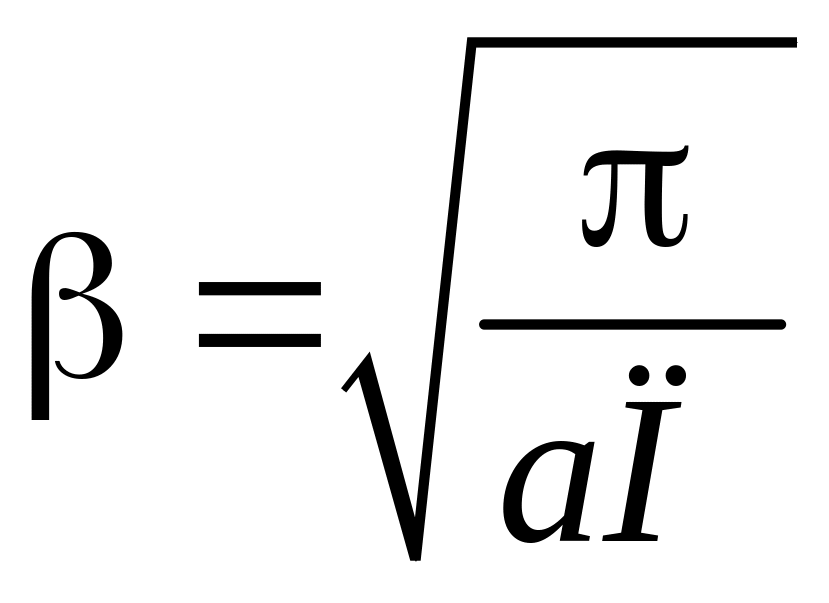отримуемо
t2
t1
=
.
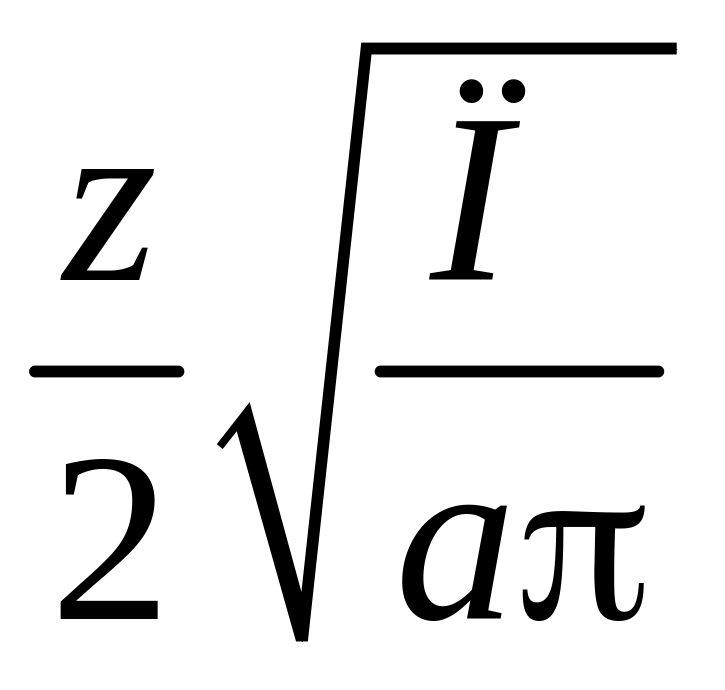(24)
Час запізнення екстремальних величин температури ґрунту з глибиною прямо пропорційно залежить від глибини та від періоду коливань в ступені 0,5 і обернено від коефіцієнта температуропровідності в ступені 0,5.
Добові коливання на глибини 10 см запізнюються на 2-3 години. У річному ході запізнення складає місяць і більше на 1м глибини.
Значення амплітуди та глибини проникнення коливань температури дуже залежать від властивості ґрунту. Так зсув по фазі або час запізнення максимуму температури з глибиною відносно цього моменту на поверхні складає у сухому ґрунті 5,7 години, у ґрунті помірної вологості 3,6 години, у дуже вологому 3,1 години. Глибина проникнення добових коливань температури змінюється від 35 до 100 см, запізнення наступу максимальних та мінімальних значень у середньому дорівнює 2-3 години на кожні 10 см глибини.
Річні коливання температури ґрунту залежать від широти. Так у високих (полярних) широтах вони досягають глибини 5-10 м, а у середніх та низьких (субтропічних) 8-24 м, іноді 30 м.
Закони поширення температурних коливань у ґрунті дозволяють визначати температуропровідність ґрунту таким чином
,
(25)
де z = z2 z1 , [a]= м2/с.