Необходимое и достаточное условие экстремума.

1. Необходимое условие экстремума

Теорема: Если в точке дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю:

.

Геометрически равенства означают, что в точке экстремума касательная плоскость к поверхности, изображающей функцию z=f(x,y) , параллельна плоскости Оху , т.к. уравнение касательной плоскости есть .

Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует.

Например, функция имеет максимум в точке О (0;0), но не имеет в этой точке частных производных.

Точка, в которой частные производные первого порядка функции z=f(x;y) равны нулю, т. е. называется стацио­нарной точкой функции z=f(x;y).

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.

В критических точках функция может иметь экстремум, а может и не иметь.

Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума.

Рассмотрим например, функцию z=xy. Для нее точка О(0,0) является критической. Однако экстремума в ней функция z=xy не имеет ,т.к. в достаточно малой окрестности точки О(0,0) найдутся точки, для которых (точки 1 и 2 четвертей) и (2 и 3 четвертей).

Таким образом, для нахождения экстремумов функции в данной области необходимо каждую точку функции подвергнуть дополнительному исследованию.

2) Достаточное условие экстремума

Теорема. Пусть в стационарной точке и некоторой ее окрестности функция z = f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке значения , , .

Обозначим:

Тогда:

1. если , то функция z=f(x;y) в точке имеет экстремум: максимум, если ; минимум, если ;

2. если , то функция z=f(x;y) в точке экстремума не имеет;

3. если , то функция z=f(x;y) в точке может иметь экстремума, может не иметь. Необходимо дополнительное исследование.

Пример 1. Найти экстремум функции .

Решение. , . Точки, в которых частные производные не существуют, отсутствуют.

Найдем стационарные точки, решая систему уравнений:

, М₁(6;3) и М₂ (0;0).

Находим частные производные второго порядка данной функции , , . В точке М₁ (6;3) имеем: А=-18, В= 36 , С=-108, АС-В² =648,

Так как , то в точке М₁ функция имеет локальный максимум: z_max=z(6;3)=27.

В точках М₂ (0,0): А=0 , В=0 , С=0 .

Проведем дополнительно исследования. Значение функции в точке М₂ равна нулю: z(0,0)=0. Можно заложить, что z=-y⁴<0 при x=0,y0; z=-x³ >0 при x<0,y=0.

Значит, в окрестности точки М₂(0,0) функция z=f(x;y) принимает как отрицательные, так положительные значения.

Следовательно, в точке М₂ функция экстремума не имеет.

Наибольшее и наименьшее значение функции в замкнутой области

Пусть функция z=f(x;y) определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторых точках своего наибольшего M и наименьшего m значении (глобальный максимум). Эти значения достигаются функцией в точках, расположенных внутри области , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значения дифференцируемой в области функции z = f(x;y) состоит в следующем:

1.Наити все критические точки функции, принадлежащие , и вычислить значение функции в них;

2. Найти наибольшее и наименьшее значение функции z = f(x;y) на границах области.

3. Сравнивать все найденные значения функции и выбрать из них наибольшего M и наименьшего m значении.

Пример 2. Найти наибольшее и наименьшее значение функции в замкнутой области, ограниченной линиями: , х=1, х=2, у=-1,5 (рисунок 2)

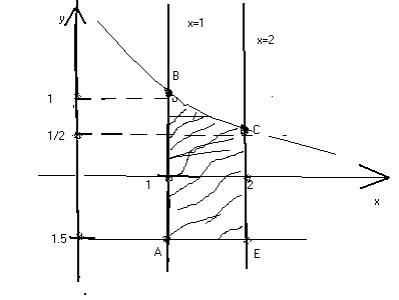
Решение:

1. находим критические точки

Решением системы являются точки: (0;0) , (-1;0) , (0;-1), .

Ни одна из найденных точек не принадлежит области .

2. Исследуем функции z = f(x;y) на границе области, состоящей из участков АВ, ВС, СЕ, ЕА.

На участке АВ: , где y [-3/2; 1] , y=-1, z(-1)=-1,

z(-3/2)=-3/4, z(1)=3.

На участке ВС: , x [1; 2]; x₁=1; x₂ =-1[1; 2],

Z (1)=3, z(2)=3.5.

На участке СЕ: , y [-3/2; 1/2] , 4y+6=0, y=-3/2, z(-3/2)=-4.5, z(1/2)=3.5.

На участке АЕ: , x[1;2],

-3x+3/4=0, x=1/4[1;2], z(1)=-3/2, z(2)=-4.5.

3. Сравнивая полученные результаты, имеем:

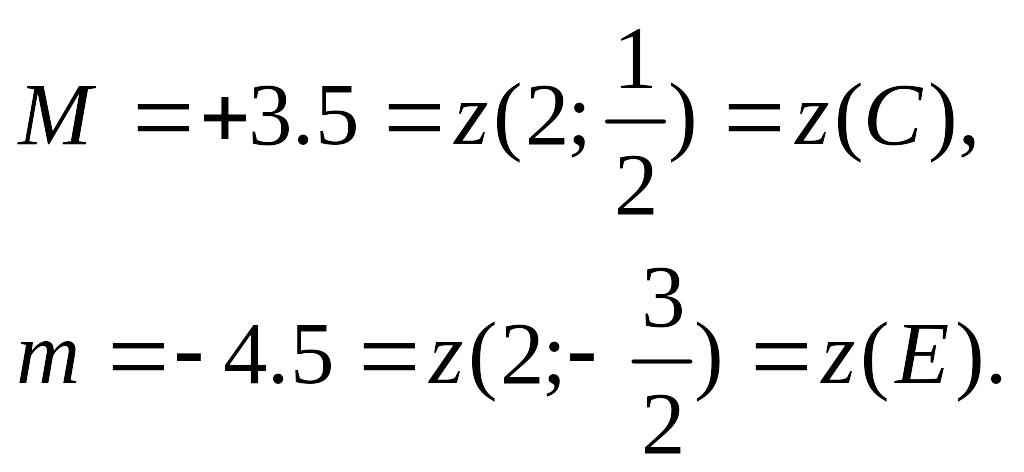
Вопросы для самоконтроля:

1. Определение предела функции двух переменных.

2. Непрерывность функции двух переменных.

3. Частные производные 1 порядка.

4. Геометрический смысл частных производных функции двух переменных.

5. Частные производные высших порядков.

6. Условия дифференцируемости функции.

7. Формул полного дифференциала в приближенных расчетах

8. Наибольшее и наименьшее значения функции

9. Условия экстремума.