V2: Дифференциальные уравнения с разделяющимися переменными.
I:
S: Общий интеграл дифференциального уравнения
имеет
вид …
-:
-:
+:
-:
I:
S:
Общее решение дифференциального
уравнения
имеет вид
…
-:
+:
-:
-:
I:
S:
Общее решение дифференциального
уравнения
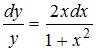имеет вид …
-:
-:
13
-:
+:
I:
S:
Общее решение дифференциального
уравнения
при
имеет вид …
-: ,
-:
,
-:
,
+:
,
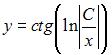
I:
S:
Общий интеграл дифференциального
уравнения
имеет вид…
-:
-:
+:
-:
I:
S: Общий интеграл дифференциального уравнения
имеет вид…
-:
-:
+:
,
14
-: I:
S:
Общее решение дифференциального
уравнения
имеет вид
-:
-:
+:
-: I:
S: Общее решение дифференциального уравнения при имеет вид …
-: , -: ,
-: ,
+: , I:
S: Общий интеграл дифференциального уравнения
имеет вид …
-:
-:
-:
+:
I:
S: Общий интеграл дифференциального уравнения
имеет
вид …
-:
,
15
+:
,
-:
,
-:
,
I:
S: Общий интеграл дифференциального уравнения имеет вид…
-:
-:
+:
-:
V2: Однородные дифференциальные уравнения
I: |
|
|
S: Общий интеграл дифференциального уравнения |
имеет вид |
|
… |
|
|
-: |
|
|
+: |
|
|
-: |
|
|
-: |
|
|
I: |
|
|
S: Общее решение дифференциального уравнения |
имеет вид … |
|
-: |
, |
|
-: |
, |
|
16
+: ,
-: ,
I:
S:
Дифференциальное уравнение
путѐм введения
новой
неизвестной функции
приведено к уравнению с разделяющимися
переменными. Тогда полученное уравнение
имеет вид …
-:
-:
-:
+:
I:
S:
Частный интеграл дифференциального
уравнения
для начального условия
имеет вид …
-:
-:
+:
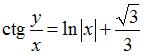
-: I:
S: Однородное дифференциальное уравнение первого порядка решается с помощью замены:
-: x zy
17
+: z y x
-: y z x
-: z x y
V2: Линейные неоднородные дифференциальные уравнения первого порядка.
I:
S: Общее решение дифференциального уравнения имеет вид …
+: ,
-:
,
-: ,
-: ,
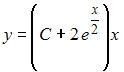
I:
S:
Общее решение дифференциального
уравнения
имеет вид …
-:
,
+:
,
-:
,
-:
,
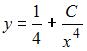I:
S:
Общее решение дифференциального
уравнения
имеет вид …
+:
-:
18
-:
-:
I:
S:
Решение задачи Коши
имеет вид …
+:
-:
-:
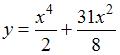
-: I:
S:
Общее решение дифференциального
уравнения
имеет вид …
-:
-:
-:
+:
I:
S: Общее решение дифференциального уравнения имеет вид
-: -: +:
-: I:
19
S:
Общее решение дифференциального
уравнения
имеет вид
+:
-:
-:
-:
