2.4. Вариация Аллана как алгоритм одноканальной обработки данных

Гироскоп и акселерометр рассматриваются, как объекты серьезного научного исследования, в которое включается выдвижение гипотез о содержании в погрешностях отдельных составляющих со специфическими характеристиками, свойственными различным факторам, таким, как квантование сигналов по уровням, дискретизация по времени, тепловые шумы, влияние внешних вибраций, старение и пр. При таком подходе встают и могут решаться задачи обнаружения значимости различных факторов, выявления степени их влияния на результирующую точность при достаточно общих представлениях о свойствах приборов, которые в формализованном виде задаются единой, комбинированной моделью, содержащей несколько составляющих.

Такой подход в частности реализуется при испытаниях точных генераторов с использованием программы обработки данных, в которых используется алгоритм вариации Аллана [хх] (в дальнейшем – просто алгоритм Аллана, используется также термин «двухвыброчная дисперсия отклонения»). Этот алгоритм, первоначально использовавшийся в очень узкой области, при определении характеристик специальных генераторов, в первую очередь нестабильности частоты [хх], рекомендован в ряде стандартов международной ассоциации инженеров электриков (IEEE Std 647-1995, IEEE Std 952-1997, IEEE Std 1139-1988, IEEE Std 1554-2005). Правда в тексте каждого стандарта он упоминается он упоминается всего два раза и он явно не находится в центре внимания, а по косвенным данным, смысл его остается непонятым. Кроме того, он рекомендован в ряде российских нормативных документов. При использовании любых стандартов следует иметь в виду, что в соответствии с действующим Законом РФ «О техническом регулировании» от 2002 года принят принцип добровольности стандартизации даже для нормативных документов в статусе ГОСТ Р, не говоря уже о зарубежных, так что не может идти речь об обязательности его применения, по крайней мере имеется свобода выборочного использования его положений. Поэтому необходим тщательный анализ предложений по использованию его разделов при обработке результатов испытаний микромеханических приборов в ЦНИИ «Электроприбор». В любом случае с алгоритмом Аллана нужно разбираться, что и делается ниже.

Вариация Аллана σ[n], как функция целочисленного аргумента п была введена первоначально [] для дискретной последовательности (или дискретизированного процесса) х[1], х[2], х[3], . . cледующим образом

σ[n] ={(2n -1)^-1 (Σ(х[i] - х[i+n])²}^½ ≈ {(2n)^-1 (Σ(х[i] - х[i+n])²}^½

Иногда в литературе вариацией (или девиацией) Аллана называется квадрат этой величины, т.е σ²[n]. Однако за определение вариации Аллана удобнее и правильнее принять выражение (), поскольку σ[n] линейно зависит от масштаба значений х[1], х[2], х[3]. Из такого исходного определения следует, что вариация Аллана в определенном смысле характеризует среднеквадратичное значение разностей, а при малых п - первой производной или скорости изменения. Важным является то, что вычисляется зависимость нормы приращений, следовательно, можно рассчитывать на то, что подобное преобразование можно применять не только к процессам, априори стационарным, но и к нестационарным процессам со стационарными приращениями. В литературе встречается еще один вариант построения преобразования, аналогичного алгоритму Аллана, но не для первой, а для второй производной. Тогда вместо ()

σ[n] ≈ {(n) ^-1(Σ(х[i] - 2х[i+n] + х[i+2n])²}^½

Из определения (), в частности, следует неотрицательность вариации Аллана. Вариация Аллана представляет алгоритм чисто эвристический, нельзя говорить о его обосновании из каких-либо общих принципов, можно попытаться установить общую логику построения и оценивать пользу от его применения на конкретных примерах. Вариация Аллана в форме () может использоваться непосредственно, без всяких изменений, если процесс задан дискретными значенииями через равные интервалы времени, но может рассматриваться, как исходный пункт для дальнейших обобщений.

Рассмотрим некоторые важные частные случаи для классических моделей дискретных случайных процессов, получаемых из непрерывных. Простейшая модель непрерывного белого шума, естественно, не годится из-за бесконечности дисперсии. Предположим, что преобразованию подвергается реализация коррелированного стационарного процесса. При стационарности случайного дискретизированного процесса (центрированность не требуется) вариация Аллана, вычисленная по формуле (), выражается через корреляционную функцию R[n] непрерывного процесса следующим образом

σ[n] ={(2п)^-1 (R[0] - R[n])}^½

Разность (R[0] - R[n] начинается с нуля, поэтому при n =0 имеет место неопределенность. Очевидно, что для недетермирнированного стационарного процесса с конечной дисперсией при n→∞ имеем σ=0, в частности она может быть монотонно убывающей.

σ[n] ={(2п)^-1 (R[0] - R[n])}^½

Для непрерывного процесса при малости интервала дискретизации по сравнению с интервалом корреляции процессов с дробно-рациональными спектральными плотностями можно использовать полиномиальную локальную (вблизи максимума в нуле) аппроксимацию разности корреляционных функций

R(0) – R(τ) ≈ R(0){1 – α| τ | - β τ ² - γ τ ⁴ . . .}

Естественно, эта функция является четной по аргументу τ, а разложение справедливо для достаточно малых τ, значительно меньших интервала корреляции. При использовании этого выражения достаточно обрезать ряд разложения после первого слагаемого из не равных нулю и зависящего от τ.

Степень τ в первом, неравном нулю слагаемом определяет важные свойства вариации Аллана в простейшем варианте. Если α≠0, то процесс имеет конечную дисперсию, но является недифференцируемым. Если α=0 но β ≠0, то первая производная и ее дисперсии конечны, и тогда коэффициент β как раз определяет дисперсию производной.

При построении зависимости σ[n] в логарифмической сетке можно начинать с очень малых значений n, т.е. с n=1, при этом малы отличия корреляционной функции от начального значения.

Заметим, что при обработке экспериментальных данных для получения коэффициентов выражения () интервал между отсчетами должен быть значительно меньше времени корреляции процесса. Независимо от дальнейшего развития идеи, подобного рода представление разности {R(0) – R(τ)}, а следовательно, вариации Аллана в форме () полезно при исследовании очень медленно изменяющихся процессов, при наблюдении которых можно получать отсчеты только на интервалах, значительно меньших интервалов корреляции. Использование слагаемого R(0)β τ² позволяет без сложных вычислений оценивать точность простейших алгоритмов экстраполяции на малые интервалы времени стационарных сигналов, что используется при формировании поправок на постоянные составляющие ошибок. Однако сложилось так, что развитие алгоритма Аллана производилось в направлении обобщения на нестационарные сигналы, характеризуемые степенными спектральными плотностями.

Буквальным и наиболее простым способом является замена дискретной переменной п непрерывной переменной t. Тогда преобразование будет иметь вид

нет выражения

Для его использования нужна конечность дисперсии, что практически исключает возможность работы с шумами высоких уровней.

Направление дальнейшей проработки алгоритма Аллана применительно к непрерывным процессам заключается в том, чтобы получить из () меру производной на больших интервалах, для чего необходимо предварительное сглаживание или осреднение по определенным интервалам времени. При этом дискретные отсчеты заменяются осредненными значениями (в зонах соответственно начала и конца интервала), а суммы – интегралами. В зависимости от способа и параметров алгоритма осреднения статистическая обработка непрерывных реализаций может осуществляться по-разному нескольких вариантах. Например, можно осуществлять осреднение на малых интервалах времени вблизи концов интервала (0, t). Однако в качестве основного следует считать следующий вариант представление вариации Аллана

σ_А (t) = {t^-3∫[ Q(t, τ) x(t - τ)]² dτ}^½ = t^-3/2{∫[ Q (t, τ) x(t - τ)]² dτ}^½

где весовая функция

Q (t,τ)= +1 при 0< τ< ½ t

Q (t,τ)= -1 при ½ t < τ< t

Здесь разность начального и конечного значений функции х(t) на интервале (0, t) заменяется разностью результатов равномерного осреднения отдельно на первой и второй половинах (они берутся с противоположными знаками), так что в конечном счете осреднение осуществляется на всем интервале (0, t). Структурная схема такого преобразования представлена на рис.

Не хватает рисунка

Выбор множителя t^-3/2 в значительной мере произволен, от этого зависят наклоны участков диаграммы Аллана.

Часто вариация Аллана имеет более сложный вид

σ_А (t) = t^-3/2{∫[ Q (t, τ) x(t - τ)]² dτ}^½

где весовая функция

Q (t,τ)= +1 при 0< τ< ½ t

Q (t,τ)= -1 при ½ t < τ< t

В структуре такого представления важным является двукратное интегрирование, которое сначала осуществляется в интегральном линейном преобразовании внутреннего интеграла свертки, а затем интегрированием квадрата результата первого преобразования. Необходим содержательный анализ того, какие преимущества дает второе интегрирование.

Алгоритм вариации Аллана, применяемый в реальном времени к единственной непрерывной реализации процесса x(t) произвольной длительности t, представляется в виде нестационарного интегрального преобразования

Введенные ранее в п. 4 масштабированная весовая функция W(t, τ)= t^-½Q (t, τ) при этом принимает дискретные значения ± t^-½. Это преобразование является нестационарным; характерным для весовой функции именно для алгоритма Аллана является кусочное постоянство знака весовой функции Q(t, τ) , она принимает только значения ±1, а ее изменение происходит ровно посередине интервала (0, t). Трансформация масштабированной весовой функции W(t, τ) по аргументу τ при различных значениях параметра t происходит так, как показано на рис.

Таким образом, весовая функция сохраняет форму и подвергается преобразованию подобия (растяжения по оси аргумента). Вид масштабированной весовой функции W(t, τ)=t^-3/2Q (t, τ), показывает, что при увеличении интервала времени t веса текущих значений сигналов уменьшаются обратно пропорционально t^3/2. Весовые функции линейных преобразований подобного вида (но антисимметричные относительно середины с однократной сменой знака) типичны для операций типа дифференцирования со сглаживанием. Преобразование хотя и является нелинейным, в частности, при любых знаках и переменах знаков x(t) его результат положителен, но обладает некоторыми важными свойствами линейного (в частности, оно линейно по масштабному коэффициенту переменной x(t)).

Однако важно, что осреднение в () является двойным, последовательным. Необходимость именно двойного осреднения подлежит обсуждению.

Принципиально возможны следующие варианты организации процедуры вычисления вариации Аллана.

Преобразование может осуществляться за один проход по всей, единственной реализации процесса от начального момента t =0 нестационарным преобразованием, определяемым масштабированной весовой функцией W(t, τ). В результате получается весь график диаграммы Алана и определяются коэффициенты (уровни) различных составляющих. Такой вариант приспособлен для работы в реальном времени и тогда преобразование разворачивается во времени (по текущему аргументу t) и так же воспроизводятся результаты. При этом отрезки ломаной появляются друг за другом, первые строятся за малые интервалы времени, последующие требуют все большей длины. Особенностью такого преобразования является необходимость запоминания растущих объемов отсчетов (точек) реализации. Однако имеются перспективы построения рекуррентных вариантов процедуры, для которых объем данных, которые нужно запоминать, не растет с увеличением времени. Если строятся несколько диаграмм Аллана (каждая по своей реализации), то осреднение производится при одинаковых значениях аргумента.

Преобразование осуществляется ретроспективно, поэтапно, с предварительным разбиением всей реализации большой длительности Т по сериям отрезков, длины которых t_i , для которых выбирается ряд (например, геометрическая прогрессия с заданным показателем, т.е. t_i+1 = kt_i или t_i = kⁱt_o). На каждом отрезке в одной серии отрезков одинаковой длины t_i осуществляется преобразование, после чего результаты по отрезкам одной длины (серии) осредняются. Очевидно, что при этом для малых значений t_i получается большее число отрезков. Результаты осреднения по сериям осредняются. Однако такой подход, безусловно справедливый при обработке стационарных процессов, должен быть подробно исследован применительно к различным типовым видам нестационарностей, присущих моделям смеси, используемой в описаниях диаграммы Аллана.

После выбора ряда значений t_i , как и в п. 2 программно реализуются стационарные фильтры с весовыми функциями W(t, τ). Каждое подобное преобразование может строиться, как комбинация двух смещенных друг относительно друга на время t_i преобразований типа скользящего среднего. Другой путь – переход от весовой функции к передаточной функции, которая, однако, не будет дробно-рациональной и придется ограничиться приближенным представлением. Используемые таким образом фильтры будут относиться осуществлять операции типа дифференцирования со сглаживанием. Реализация процесса прогоняется через эти фильтры, в результате чего получаются дискретные значения вариации Аллана. Подобная процедура может быть реализована, как последовательная или как параллельная. Как и в п. 2 способ безусловно можно использовать лишь при обработке стационарных процессов, но необходимо специальное обоснование для типовых нестационарностей.

Во всех вариантах могут подвергаться преобразовываниям несколько реализаций полученных или для одного и того же прибора, но разделенных большими временными интервалами (тогда оцениваются стабильность характеристик или «старение»), или для разных приборах (тогда оцениваются индивидуальные различия). В подобных случаях целесообразно дополнительно осуществлять еще одну ступень осреднения (по реализациям). Однако определенную ценность может представлять сопоставление данных, полученных для разных реализаций, и оценивание разбросов.

В настоящее время выпускается аппаратура статистического анализа с необходимым программным обеспечением, позволяющем вычислять вариацию Аллана (например, анализатор шумов и вариации Алана ADEV фирмы Symmetricon). Соответствующие программы есть в пакете . . .

Очевидно, что при ретроспективной обработке конечных массивов данных аргумент t ограничивается только длительностью реализации, располагаемым временем Т регистрации процесса. Видоизмененный вариант вариации Аллана, исходно определяемый выражением () и обладающий теми же свойствами, представляется преобразованием, где при той же весовой функции вместо сочетания функция квадрата подынтегрального выражения с последующим извлечением корня вводится функция модуля

σ_А1 (t) = t^-3/2∫ |Q (t, τ) x(t - τ)| dτ

Это заметно облегчает вычисления, придает свойство робастности, устойчивости по отношению к редким выбросам высоких уровней, а все особенности преобразования сохраняются. Принято представлять результат в логарифмической сетке, что практически означает умышленное дополнительное введение в преобразование нелинейности определенного вида к базовой нелинейности (квадрат, потом извлечение квадратного корня или вместо этого операция модуля), вследствие этого теряется знак функции и результат преобразования при любом значении аргумента всегда положителен. Как отмечалось в п. 4, это характерно и целесообразно лишь для алгоритмов, используемых только для определения характеристик знакопеременных, недетерминированных составляющих сигналов.

Для весовой функции Q(t, τ) в вариации Аллана важным является свойство

∫ Q(t, τ) dτ =0,

которое справедливо для любых t. Это свойство проявляется в том, что вариации Аллана не дает возможности оценивать постоянную составляющую (смещение нуля). В некоторых приложениях это, возможно, является достоинством, предположительно весовая функция алгоритма Аллана была специально построена так, чтобы исключить смещение нуля, но применительно к большинству рассматриваемых здесь приложений является явным недостатком.

Преобразование Аллана может быть применено к сигналам с различными свойствами; интересно просмотреть, что получается для сигналов различных видов, например, форм детерминированных процессов или свойств недетерминированных процессов, в рамках аттестации алгоритмов, идеология которой представлена в серии публикаций []. Подобная работа по аттестации алгоритма Аллана была проведена Т.Н.Сирой [], некоторые результаты для сигналов, представимых аналитическими выражениями определенного вида приведены ниже.

Очевидно, что использование вариации Аллана имеет практический смысл тогда, когда результат этого преобразования наглядно представляется в виде функции достаточно простого вида, отчетливо идентифицируемого по графическому изображению. Это имеет место для некоторых видов недетерминированных процессов, например, для белого шума или интеграла от белого шума. С другой стороны, по отношению к детерминированным процессам, например, для синусоиды результат трудно идентифицируем, представляет затруднение даже оценка частоты. Из этого следует, что важным критерием выбора весовой функции является простота восприятия графического представления результата преобразования. Это особенно важно, если преобразуемый процесс является комбинированным, в нем имеется несколько составляющих различной формы или с различными свойствами.

Сам принцип построения таких преобразований комбинированных процессов, для которых составляющие этих процессов явно проявляются в графике результата преобразования, Подобный прием предлагался автором для использования в теории автоматического управления при представлении логарифмических амплитудно-частотных характеристик при параллельном соединении звеньев, а также при построении спектральных плотностей сумм нескольких составляющих сигнала при представлении огибающей сверху []. Этот же прием может быть использован не только при обработке экспериментальных данных, но и при представлении результатов аналитических исследований, также при математическом моделировании.

В большинстве литературных источников алгоритм Аллана хотя и рассматривается, как универсальный, но рекомендуется для решения задачи представления результата преобразования, когда в сигнале имеется вполне определенное число составляющих со вполне определенными свойствами. В основоположных работах Аллана и его последователей было предложено применить его для преобразования сигнала в виде смеси при задании модели анализируемого сигнала в виде смеси (суммы) составляющих вида

x(t) = x₁(t)+ x₂(t)+ x₃(t)+ x₄(t)+ x₅(t)

Здесь x₁(t)– случайная составляющая типа белого шума (для ДУС - по угловой скорости), x₂(t) - случайная составляющая типа фликкер-шума, который иногда называется «розовым» шумом (со спектральной плотностью, обратно пропорциональной частоте ω), x₃(t) –нестационарная переменная случайная составляющая типа винеровского процесса, т.е. интеграла от белого шума со спектральной плотностью, обратно пропорциональной ω² (она каких-либо содержательных пояснений трактуется, как нестабильность нуля), x₄(t) – случайная составляющая типа интеграла от фликкер-шума со спектральной плотностью, обратно пропорциональной ω³, x₅(t) ) = Аt - неслучайная составляющая, изображающая линейный во времени дрейф. Отметим, что алгоритм Аллана является эвристическим, он совсем не требует именно такого состава и способа описания составляющих в смеси ().

Интересно представить вид изменяющееся во времени условной зоны, в которой преимущественно находятся реализации процессов (она может быть шириной, например, 3σ или 2σ). Вид части, положительной половины этой зоны (симметричной относительно оси времени) ограничен в логарифмической сетке сплошными линиями, а зон составляющих – пунктирными прямыми (номера соответствуют слагаемым в выражении ()) представлен на рис.. Начальный, горизонтальный (на нем ширина указанной зоны постоянна) , который должен был бы белому шуму, построен для стационарного случайного процесса с конечной дисперсией (этим самым предполагается, что по выходу осуществляется определенное сглаживание, что всегда имеет место на практике). Прямолинейные участки (в логарифмической сетке), которые определяют расширение зоны) могут быть построены, если модели составляющих и их параметров известны. Но если разделение на составляющие заранее неизвестно, сами границы для суммарной ошибки могут быть построены непосредственно по результатам испытаний, и это достаточно для того, чтобы оценивать интервалы времени, на которых ошибки не превышают заданный уровень (показано штриховой линией). Если интерес представляют не очень большие диапазоны по уровням и по времени (что характерно для большинства приложений), то совсем не обязательно производить построение в логарифмической сетке. Определение наклонов участков при этом не является обязательным. Как отмечалось в п. , подобный подход является традиционным для теории измерений.

Следует в первую очередь обратить внимание на то, что из пяти составляющих четыре являются недетерминированными, а из них, в свою очередь, только одна, а именно, первая является безусловно стационарной (а именно, представляет собой белый шум), а остальные характеризуются нарастанием дисперсии во времени, т.е. для них установившиеся дисперсии не существуют. Это противоречит физически понятной и привычной гипотезе о том, что в неизменных условиях уровень показателей точности не меняется. Включение в рассмотрение составляющих, уровень которых растет все быстрее, может быть объяснено стремлением учесть незаметные, проявляющиеся только на очень больших интервалах лавинообразные деградационные процессы. Однако их модели не могут быть введены чисто формально. Отметим, авторы давно и успешно использовали степенные локальные представления спектральных плотностей в виде степенных функций (в [] они были названы условными спектральными плотностями), но только с целыми четными показателями при синтезе оптимальных характеристик преобразований в задачах, приводимых к определению полезных сигналов на фоне шумов. Однако подобные представления, как локальные аппроксимации спектральных плотностей вблизи определенных точек использовались только на промежуточных этапах вычислений, но не при задании исходных данных и не в конечных результатах.

В основоположных работах, в которых описываются результаты использования вычислений вариации Аллана, особое внимание обращается на третью составляющую, которая, как интеграл от белого шума, нестационарна, характеризуется дисперсией, линейно нарастающей во времени, она, по-видимому, действительно представляет первостепенную важность для экспериментального исследования электронных систем определенных классов. В работах прикладного характера, в которых алгоритм Аллана используется без какого-либо предварительного содержательного анализа, обращается внимание исключительно на ординату этого горизонтального отрезка, и именно эта ордината приводится, как конечный результат исследования.

Отметим, что по крайней мере две составляющие (фликкер-шум и интеграл от фликкер-шума) не являются традиционными для описания случайных процессов в теории автоматического управления, а также погрешностей приборов, причем не только рассматриваемых навигационных датчиков, применительно к навигационным приборам их введение в модель не связывается с определенными физическими процессами; при этом для этих составляющих не могут быть записаны дифференциальные уравнения связи с порождающими белыми шумами. Это может вызвать серьезные трудности при математическом моделировании, когда при освоении алгоритма Аллана желательно получить имитационным моделированием по реальным данным диаграмму в полном виде, как на рис. , поскольку формирование фликкер-шума из порождающего белого шума хотя и возможно, но не элементарно. Наиболее распространенным способом является пропускание белого шума через систему широкополосных фильтров со специально подбираемыми частотами среза. При конечном числе таких фильтров приближение с определенной точностью, которая может быть задана, свойств генерируемого процесса к фликкер-шуму или другим «окрашенным» шумам получается в конечном диапазоне частот. Предварительно не зная диапазон частот доминирования каждой из составляющих этот диапазон все же нужно заранее хотя бы грубо оценивать.

При отсутствии обоснованных априорных доводов и аргументов в пользу существования и включения в комбинированную модель именно фликкер-шума, можно было бы задать свойства одной из составляющих (гипотетической) спектральной плотностью в виде степенной функции S(ω)= a²ω^k с произвольным, целым или дробным показателем степени k или несколько подобных составляющих. Возможности их использования при аппроксимации данных по экспериментально получаемым спектрам, обсуждаются специалистами в различных разделах физики (так называемые «цветные шумы»). С другой стороны, можно было бы добавить детерминированные составляющие с различными показателями степеней.

Принято считать, что при преобразовании смеси ожидаемый результат вычисления вариации Аллана графически должен приближенно изображаться в виде суммы составляющих. При значительном разнесении составляющих ошибок по уровням результат суммирования, как функция текущего времени t представляется в виде гладкой кривой, непрерывной зависимости, в виде диаграммы Аллана, которая, однако, как предполагается, будет в логарифмической сетке при изменении аргумента (времени) на несколько порядков хорошо аппроксимироваться ломаной (рис. ), прямолинейные участки которой имеют определенные наклоны.

При этом участки (в действительности не имеющие углов при сопряжении, а плавно сопрягаемые) будут иметь определенные наклоны, причем уровни положения отрезков соответствуют масштабным коэффициентам (множителям) при составляющих. Это основано на представлении, что при разворачивании во времени (увеличении параметра t) получается последовательность интервалов, на каждом из которых проявляется преимущественно одна составляющая, намного большая по уровню именно на этом интервале по сравнению с остальными. Номера прямолинейных участков на рис. соответствуют номерам составляющих в выражении (). Обычно наклоны участков обозначаются соответственно числами -1, -½, 0, +½, +1. Это непосредственно следует из задания модели в виде ().

Вставка моя

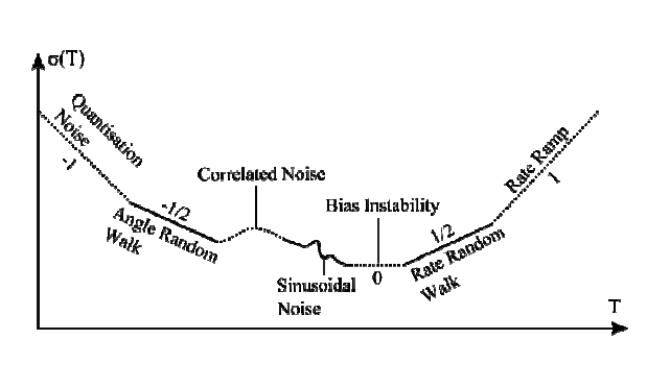
Из анализа диаграммы Аллана видно, что участок с нулевым наклоном позволяет оценивать нестабильность дрейфа (Bias Instability), величина которого имеет размерность [⁰/ч]. Участок с наклоном -½ позволяет оценить максимальный случайный уход по углу (в ⁰/√ч), английское сокращение ARW (буквально «случайное блуждание по углу»). Например, при определении времени, в течение которого уход по углу составит величину , следует воспользоваться выражением t = (/ARW)². Наверно, надо несколько таких примеров использования паспортных данных МЭМС.

Но к построению диаграммы Аллана можно подойти и с другой стороны, а именно, с позиций аппроксимации экспериментальных данных при использовании алгоритма Аллана. Диаграмму Аллана можно рассматривать, как линейную в логарифмическом масштабе сплайн-аппроксимацию экспериментальных данных, причем при вполне определенных наклонах линейных участков (обычно задаваемых, как указано ранее, числами -1, -½, 0, +½, +1). Этому соответствует вполне определенная подобная, кусочно-линейная в логарифмическом масштабе аппроксимация спектральной плотности с участками наклонов, кратных 20 дБ/дек. При таком представлении и диаграммы Аллана, и спектральной плотности точки сопряжения подбираются из услоий наилучшего приближения к экспериментальны данным. В обоих случаях предполагается, что наклоны участков изменяются монотонно в сторону увеличения, т.е. контур ломаной является вогнутым. Однако можно не вводить в модели смесей составляющие, нетрадиционные для прикладных наук. Так, можно предположить, что в процессе отсутствуют окрашенные шумы типа фликкер-шума и интеграла от него. Например, если смесь включает только три, нечетные составляющие выражения (), а именно, белый шум, интеграл от белого шума и линейно-нарастающую детерминированную составляющую, то диаграмма Аллана будет иметь такой вид, как показано на рис. . Такой же вид будет у диаграммы, если фликкер- шум или иные «цветные» шумы хотя и присутствуют, но они имеют низкие уровни и применительно к данному алгоритму они являются ненаблюдаемыми.

Необходимо напомнить, что естественное, но приближенное разделение сложной зависимости по прямолинейным участкам в логарифмических сетках получается и используется преимущественно при построении скелетных логарифмических амплитудно-частотных характеристик динамических систем. Используя принятую там градацию шкал на диаграмме Аллана рис. эти наклоны кратные 10 децибелам на декаду, их следовало бы обозначать – 20 дБ/дек, -10 дБ/дек, 0, +10 дБ/дек, +20 дБ/дек.

При этом идентификация каждой из составляющих осуществляется по показателю наклона асимптотически прямолинейного (практически – лишь близкого к прямолинейному в логарифмической сетке) участку, а масштабный коэффициент при – по уровню (по множителю или весу). Таким образом, в отношении недетерминированных составляющих построением диаграммы Аллана осуществляется своеобразный, очень грубый спектральный анализ с идентификацией составляющих с вполне определенными по форме аналитическими выражениями спектральных плотностей, конкретно - степенными. Но в отличие от широко распространенных анализаторов спектра он является широкополосным, причем выявляются не узкополосные, а широкополосные составляющие функциями зависимости от частоты с различными показателями. Особое внимание обычно обращается на средний, третий участок, поскольку соответствующей составляющей, представляющей собой интеграл от белого шума, придается смысл показателя нестабильности.

Практически, при работе алгоритма на одной реализации однократным проходом составляющие процесса проявляются последовательно, слева направо, причем интервалы, на которых видны эти составляющие, могут увеличиваться на порядки. Следует обратить внимание на то, что на приводимой в качестве иллюстрирующего примера диаграмме вида рис. , воспроизводимой в большинстве литературных источников, рассматриваемые интервалы времени увеличиваются на пять порядков, так что при благоприятных сочетаниях параметров первые составляющие проявляются через сотые доли секунды, а последние – через десятки часов. Поэтому подобное полное представление результатов в принципе возможно при специальных длительных исследовательских испытаниях с достаточно высокими частотами регистрации значений.

Очевидно, что применительно к типовым практическим применениям интерес представляют интервалы времени в пределах одного порядка (например, для БИНС это десятки секунд или единицы минут) и при этом определяющими является только одна или максимум две составляющие, так что определяющими для погрешностей системы на этих интервалах являются только они.

Начальные участки соответствуют недетерминированным составляющим, а последний - детерминированной. При этом первый, падающий участок теоретически имеет вид, как на рис. лишь в предположении бесконечности дисперсии шума, что отчетливо является идеализацией. При конечности дисперсии шума, приближенно квалифицированного как белый шум (что обязательно для любого реального процесса) поведение ломаной зависит от корреляционной функции, и начальный участок при очень малых интервалах времени может быть возрастающим, что изменит общую конфигурацию ломаной.

Необходимо отметить, что в логарифмической приближенно спектральная плотность S(ω) суммы недетерминированных составляющих имеет такой вид, как показано на рис. .

S(ω)

ω

Номера составляющих сигнала – те же, что и в выражении () или на графике рис. . Видно, что по отношению к диаграмме Аллана порядок участков обратный (справа налево), причем горизонтальный участок 1 соответствует белому шуму. Это и естественно, поскольку движение по оси времени в сторону возрастания соответствует движению по оси частот в сторону убывания. Наклоны участков составляют соответственно 0, -20 дБ/дек, -40 дБ/дек, -60 дБ/дек. Характерна вогнутость ломаной в том смысле, что при движении слева направо последовательные прямолинейные участки поворачиваются против часовой стрелки.

При этом существенно предположение, что детерминированные составляющие являются степенными функциями t, а спектральные плотности - степенными функциями ω. Операция логарифмирования, т.е. представления результата в логарифмической сетке, что соответствует графическому изображению, может быть включена в аналитическую запись алгоритма Аллана следующим образом

Однако это не принято.

Как отмечалось ранее, наличие составляющих процесса со спектральными плотностями, неограниченно возрастающими при ω→0 противоречит гипотезе о стационарности погрешности, и вогнутую конфигурацию рис. нельзя признать типичной. При обычном сглаживании сигнала (а следовательно и переменной погрешности) прибора на выходе, а также при прохождении случайных воздействий через любые динамические системы типичной можно признать не вогнутую, а выпуклую конфигурацию (также в логарифмической сетке), как показано на рис. . Наклоны по участкам при переходах справа налево соответственно составляют -80 дБ/дек, -40 дБ/дек, 0. Отметим, что увеличению наклона участков спектральной плотности слева направо соответствует обращению в нуль все более высоких производных корреляционной функции в нуле аргумента. Предполагается, что эта зависимость также представляется в виде ломаной, что соответствует представлению о схеме преобразования белого шума сглаживающим фильтром. Рассчитанная диаграмма вариации Аллана для спектральной плотности рис. с тремя прямолинейными в логарифмической сетке участками имеет такой вид, как показано на рис.

Рис.

Рис.

Видно, что выпуклость (понимаемая в узком смысле, имеется в виду изменение наклонов при движении слева направо, идет по часовой стрелке) кривой спектральной плотности приводит к выпуклости диаграммы Аллана в том же смысле.

Диаграмма Аллана в данном случае обладает важными качественными особенностями. По своему характеру получается зависимость обратная тому, что получалось для обычно представляемой модели сигнала в виде ().

Насколько известно, логарифмические масштабы по осям во временном представлении (при аргументе t) не получили распространения. Может найти применение представление в полулогарифмической сетке (логарифмический масштаб по вертикальной оси) переходного процесса в виде суммы экспонент

x(t) = ΣA_i exp (- α_i t)

При всех положительных A_i и α_i для случая трех составляющих процесса эта зависимость может иметь такой вид, как показано на рис.

При возможной отрицательности некоторых коэффициентов A_i для использования логарифмического масштаба предварительно в преобразовании целесообразно избавиться от знака обычным способом, а именно, использовать операции взятия модуля или возведения в квадрат. При этом может быть определенные нарушения конфигурации вблизи точек сопряжения, возможны неинформативные локальные аномалии типа провалов. Для общей конфигурации (сопряжение участков прямых в полулогарифмической сетке) знаки параметров α_i несущественны. Насколько известно, такой способ представления сумм экспонент не нашел широкого применения, но может оказаться полезным, особенно когда момент окончания переходного процесса может устанавливаться по допуску, который может изменяться в широких пределах. Аналогичным образом удобно представлять корреляционную функцию смеси составляющих, каждая из которых имеет экспоненциальную корреляционную функцию. Если же составляющие имеют знакопеременные корреляционные функции, то подобное построение имеет смысл строить для их огибающих.

Вариация Аллана, как прием, при графическом представлении результатов в виде диаграммы приспособлена для отображения сумм слагаемых, каждое из которых определяется степенной зависимостью от аргумента. Важно, что при построении вариации Аллана каждая составляющая в логарифмической сетке имеет простой геометрический образ, а именно приближенно (асимптотически) представляется в виде прямой, причем наклон прямой определяется только показателем степени зависимости этой составляющей от времени (или ее спектральной плотности от частоты ω), а уровень определяется соответствующим весовым коэффициентом.

При желании модель процесса могут быть дополнены еще несколькими составляющими, причем спектральная плотность каждой изображается в логарифмической сетке прямой с любым наклоном (а именно, S(ω) =Aω^k) или детерминированной составляющей с любой степенной зависимостью от аргумента t (а именно х(t) = Bt^α при α≠0) или несколькими подобными составляющими. В обоих случаях помимо коэффициентов А и В могут быть заранее неизвестными также показатели степеней k и α, которые могут быть дробными (что может получаться при приближенном представлении результатов обработки экспериментальных данных), тогда их также можно определять по результатам обработки данных. При этом нужно учитывать, что процедура вычисления вариации Аллана не позволяет различать возрастающие детерминированные и недетерминированные составляющие при определенных соотношениях между показателями степеней спектральных плотностей и аргументе - времени.

Указанные зависимости спектральных характеристик недетерминированных составляющих (они описывают «цветные» или «окрашенные» шумы), которые часто встречаются в различных разделах экспериментальной физики и соответствующих технических приложениях, чаще всего могут рассматриваться, как приближенные, от степени приближенности на интервале определения этих составляющих зависит достоверность и точность определения параметров. Насколько известно, подобные аппроксимации спектральных плотностей считаются справедливыми только для ограниченных диапазонов частот, а различение свойств стационарности или нестационарности по полному диапазону частот (0, ∞) часто для исследователей интереса не представляет.

Если процессы представляются, как смеси подобных шумов, то построение в логарифмической сетке спектральных плотностей и диаграмм Аллана для них будет представлять собой классическую процедуру линейной сплайн-интерполяции экспериментально полученной (по точкам) зависимости. В принципе число составляющих при представлении процесса в частотном виде не ограничено. При увеличении числа составляющих можно как будто получать все более точное соответствие экспериментальным данным. Однако без содержательного обоснования на каждую составляющую их не рекомендуется включать в модель сигнала.

Чтобы избежать противоречий с мнимой нестационарностью, вполне достаточно предполагать существование и особенности аналитического представления спектральных характеристик степенными функциями только на тех интервалах, на которых они являются доминирующими, а вне этих интервалов они могут быть продолжены как угодно, в частности так, чтобы спектральные плотности были бы интегрируемыми. Подобным образом можно составляющие представить, как стационарные.

Отметим, что при представлении дробно-рациональных спектральных плотностей в логарифмической сетке она приближенно представляется в виде ломаной с наклонами, кратными 40 дБ/дек. Это означает, что на последовательных интервалах, если они достаточно большие (не менее одной декады), процесс представляется, как сумма интегралов от белого шума. И тогда несколько участков будут относиться к одному процессу.

Можно сказать, что при использовании алгоритма Аллана при благоприятных условиях осуществляется частотная селекция по временной развертке, так что на каждом из последовательных временных интервалов проявляется преимущественно одна из составляющих. Однако если в число составляющих входят такие, геометрические образы которых сложны по форме и не приспособлены для восприятия в логарифмической сетке (например, узкополосные в узких диапазонах частот), они могут и, как правило, будут портить общую картину.

Специфическими для алгоритма вариации и диаграммы Аллана являются:

- алгоритм Аллана реализуется в одноканальной схеме, составляющие и их параметры могут определяться по результатам расшифровки и интерпретации результата преобразования единственной реализации выходного сигнала, как функции времени, хотя возможно повторение по другим реализациям с последующим осреднением;

- кусочное постоянство весовой функции, это несколько упрощает реализацию алгоритма, что, впрочем, несущественно при современном уровне вычислительной техники;

- изменение знака на противоположный весовой функции посередине интервала (подобное изменение знака весовой функции характерно для стационарных операций типа дифференцирования со сглаживанием);

- одним и тем же преобразованием определяются параметры как одной из детерминированных составляющих, так и случайных недетерминированных, все составляющие являются однопараметрическими;

- сведения о различных составляющих (о соответствующих коэффициентах) появляются последовательно во времени; хотя как будто осуществляется использование всей длины реализации, но при определении коэффициентов отдельных составляющих те отрезки, на которых осуществляется определение различных составляющих, существенно (даже на многие на порядки) могут различаться;

- параметры каждой составляющей процесса определяются практически только на тех интервалах, на которых они являются доминирующими;

- последовательное во времени определение коэффициентов составляющих в той последовательности, в которой они приводятся в формуле (); при этом естественным образом проявляется на различных интервалах, положение и длина которых (в логарифмической сетке) зависят от соотношения между параметрами составляющих;

- алгоритм не привязан к определенной совокупности составляющих сигнала, состав сигнала может быть расширен или сужен.

При определенных достоинствах алгоритм Аллана обладает существенными ограничениями и недостатками:

Отчетливая картина, подобная представленной на рис. , когда отдельные составляющие могут быть достоверно выделены по последовательным интервалам времени, может иметь место только тогда, когда рассматривается широкий диапазон интервалов времени, а именно несколько порядков (не менее трех-пяти). В соответствии с этим шаг дискретизации по времени должен быть достаточно малым, так, чтобы на тех интервалах времени, на которых проявляются первые составляющие, при обработке использовалось достаточно большое число данных (отсчетов). Очень широкий диапазон представления модели процесса (несколько порядков) полезно иметь в глубоких физических исследованиях, когда не обращается внимания на прикладные задачи, а важно выявление различных источников помех, имеющих различную природу, независимо от влияния на точность решаемых задач. Однако для многих приложений по крайней мере, порядок интервалов времени вполне определен (например, для работы ММГ в составе БИНС это десятки секунд). Поэтому информация о свойствах тех составляющих, которые проявляют себя на малых (на порядок меньших) отрезках времени, не представляет практической ценности.

Одна и та же картина при представлении результатов вычисления вариации Аллана может получаться при качественно различных свойствах составляющих в смеси. Например, если вместо (), где кроме одной все составляющие недетерминипрованы, в противоположность этому в сумме имеется нескольких слагаемых все они детерминированные и представимы в виде степенных функций с целыми дробными (отрицательными и положительными показателями степенейили ), или все они знакопеременные недетерминированные с дробными показателями степеней, то на графиках могут получаться совершенно одинаковые результаты в виде кривых (приближенно ломаных). Таким образом, вариация Аллана неспособна разделять и идентифицировать, с одной стороны, знакопостоянные, в частности прогрессивно и монотонно нарастающие составляющие, а с другой стороны, недетерминированные знакопеременные, характеризующие процессы накопления случайных отклонений.

Некоторые из составляющих, если они недостаточно высоки по уровням, при использовании алгоритма Аллана могут оказаться практически ненаблюдаемыми, соответствующие участки могут при этом «проваливаться» ниже уровней смежных участков. Вопросы обнаруживаемости и идентифицируемости отдельных составляющих сигнала на фоне других составляющих требуют специальных исследований.

При приближенном характере описания свойств недетерминированных составляющих, которые в действительности характеризуются спектральными плотностями более сложного вида, чем степенными (а именно, дробно-рациональными), при использовании алгоритма Аллана на интервалах времени, на которых эти составляющие являются доминирующими, могут появляться как прямолинейные участки, так и участки ломаных. Однако частотные диапазоны, в которых эти составляющие определяются, заранее неизвестны. В то же время для оптимизации преобразований, в частности навигационных систем для установившихся режимов при использовании локальных аппроксимаций необходимо знать поведение спектральных плотностей во вполне определенных диапазонах частот, и только случайно этот диапазон может совпасть с тем диапазоном, на котором спектральная плотность будет выявлена при использовании алгоритма Аллана.

Возведение в квадрат в подинтегральном выражении упрощает графическое представление результатов преобразования, но приводит к потере знаков. Знаки несущественны для тех составляющих, в первую очередь, недетерминированных, которые заведомо имеют нулевые средние значения и являются знакопеременными. Но знаки существенны для составляющих ошибок, которые можно рассматривать, как систематические (для модели в виде () это линейный дрейф по угловой скорости). Потеря знака означает невозможность использования результатов преобразований для выработки и введения корректирующих поправок на систематические составляющие, поэтому результат может быть использована только для общего представления о том, на каких интервалах времени именно эта составляющая существенна. В то же время, если даже только ставится задача оценить значимость знакопостоянной составляющей для партии приборов, выявление преимущественного появления одного и того же знака, возможно позволит выработать обоснованные рекомендации по калибровке и регулировке.

Ненаблюдаемыми являются некоторые важные составляющие сигнала, в первую очередь смещение нуля, очень важное для некоторых из задач, перечисленных в п. 1. Это однозначно связано с выбором весовой функции интегрального преобразования, которое, как отмечалось выше, имеет смысл дифференцирования со сглаживанием. Нестабильность смещения нуля, как качественное свойство очень важно. Однако конкретный смысл составляющей модели погрешности, имеющей такое наименование, неясен; неясно, как использовать этот количественный показатель для оценки вклада соответствующих составляющих погрешностей БИНС по углам, скоростям или координатам. Обычно получается, что интервал времени, на котором проявляется нестабильность смещения нуля, далеко выходит за пределы представляющих интерес интервалов работы БИНС, на которых ошибки по скоростям и координатам

В случае построения диаграммы Аллана прогонкой по одной реализации при определении шумовых случайных составляющих, которым соответствуют первые участки графика рис. , используются сигналы только на очень коротких интервалах времени, возможно на порядки меньших максимальной используемой при преобразовании длительности реализации Т. Например, по очень короткому начальному интервалу определяется предполагаемой постоянной интенсивность белошумной составляющей. Если учесть, что реальный шум не имеет бесконечную дисперсию, а характеризуется затухающей спектральной плотностью, то в графике типа рис. реально может появиться новый участок, который может быть ошибочно идентифицирован, как новая составляющая с иными свойствами. При всем этом исключается возможность выявления и анализа такого фактора, как всегда существующая и часто практически важная относительно медленная изменчивость этой интенсивности, проявляющаяся в реализации на больших интервалах времени.

При определении составляющих, которым соответствуют последние участки графика рис. , используются сигналы на очень больших интервалах времени, имеющих порядок максимальной длительности реализации Т. На не очень больших интервалах времени (заранее неизвестно, каких) при использовании алгоритма Аллана никакие достоверные сведения об этих составляющих не могут быть получены, нужно охватить интервалы, на которых именно эти составляющие являются доминирующими (такие интервалы вообще могут отсутствовать. В частности, в вариации Алана может быть ненаблюдаем показатель нестабильности дрейфа (составляющая ).

Практическая польза от определения некоторых составляющих сомнительна. Например, хотя качественно нестабильность нуля может быть признана важной, неясно, каким образом можно использовать характеристику, имеющую такое наименование в представлении модели сигнала, при решении конкретных задач, например, в БИНС, в состав которой входит ММГ. Кроме того, указанный показатель, квалифицируемый, как нестабильность нуля, определяется на заранее неизвестном интервале времени, возможно определяемом часами или десятками часов, что очень далеко от интервалов времени, на которых должен работать БИНС.

Вследствие всего сказанного выше представляется, что алгоритм вариации Аллана ни в коем случае не может рассматриваться, как универсальный алгоритм, его можно использовать только наряду с другими, проверенными и освоенными; эти алгоритмы частично рассмотрены ранее в п. 4 и 5. Содержащиеся в ряде американских стандартов IEEE рекомендации по его использованию не может быть принята без тщательного предварительного анализа на предмет применимости в конкретных приложениях. Опыт анализа свойств вариации Аллана, принимаемой часто в качестве единственной правильной процедуры, дающей исчерпывающие представления, можно перенести на другие, столь же эвристические процедуры, которых можно предложить и рассмотреть великое множество. Алгоритм Аллана является частным случаем целого семейства алгоритмов будут рассмотрены далее в п.7.