2.2.. Алгоритмы преобразований для определения параметров детерминированных составляющих процессов

При определении коэффициентов детерминированных составляющих в многоканальных схемах алгоритмы обычно являются линейными, если неизвестные параметры являются множителями С_i при функциях f_i(t) известного вида

и_дет (t) = Σ С_i f_i(t)

Алгоритмы преобразования в каналах многоканальной схемы задаются весовыми функциями W_i(t, τ). Эти весовые функции можно и целесообразно задавать так, чтобы на выходах каналов получались оценки искомых коэффициентов, причем независимые друг от друга, т.е. имело бы место разделение, развязка по детерминированным составляющим. Условия разделения представляются в виде равенств нулю определенных функционалов от весовых функций W_i(t, τ), и поэтому наложение только этих условий оставляет широкую свободу в выборе весовых функций, и такое задание весовой функции, как в алгоритме Аллана представляет только одну из многих альтернатив.

Весовые функции также могут определяться однозначно, обычно при оптимизации по тем или иным критериям. В этих критериях может не использоваться или использоваться реальная или виртуальная информация о также присутствующих в сигналах недетерминированных составляющих, которые играют роль подлежащих устранению помех, свойства которых в данной задаче не определяются.

Приведем данные об обычно используемых алгоритмах определения коэффициентов С₁ и С₂ , представляющих собой множители слагаемых в линейно изменяющейся сумме

х_д (t) = С₁ + С₂ t

Применительно к ММГ слагаемые этого выражения представляют собой соответственно постоянное смещение нуля и линейный дрейф. Преобразование строится по параллельной схеме типа рис.5. Метод наименьших квадратов, который был бы оптимален в случае наличия белого шума, но дает хорошие результаты также и при случайных шумах с другими свойствами, дает следующие выражения весовых функций текущего преобразования

W₁(τ) = 2t^-1(2 - 3τ t^-1) W₂(τ) = 6t^-2(1 - 2τ t^-1)

Соответствующие графики (они представляют собой кусочно-линейные функции) приведены на рис. .

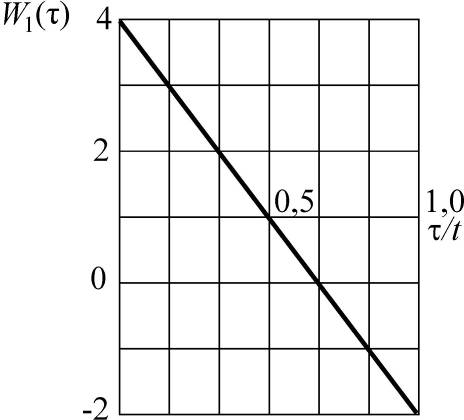
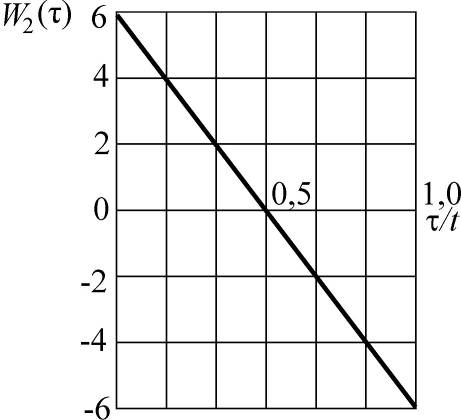
Рис.5.

При нестационарности, когда время памяти непрерывно растет, параметр t переменный. При скользящем стационарном преобразовании на интервале (t-Т, t) в приведенных выражениях весовых функциях t заменяется на время памяти Т.

Используя тот же прием, что и в рассмотренном далее, в п.5 алгоритме Аллана, можно задать весовые функции каналов кусочно-постоянными на условно единичных уровнях при одиночных в пределах интервала переменах знака в согласованные, но различные моменты времени

W₁(τ) = 1 при 0<τt^-1<2^-½ W₂(τ) = 1 при 2^-½<τt^-1<½

= -1 при 2^-½<τt^-1<1 = -1 при ½<τt^-1<1

Графики этих весовых функций имеют такой вид, как показано на рис.6

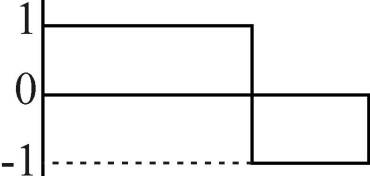
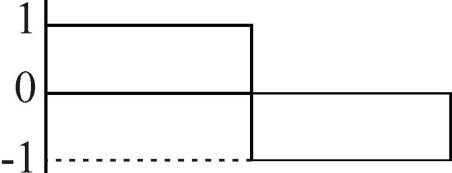
а б

Рис.6.

Как показали численные расчеты, результаты при этом результаты близки к получающимся МНК. Если допустить изменения знаков на интервалах дважды, то в выборе соответствующих моментов времени допускается определенный произвол.

В частных случаях получаются очень простые результаты. Так, если в () имеется (учитывается) только первое слагаемое С₁ (смещение нуля), то оптимальная весовая функция постоянна W₁(t,τ) = t^-1, что просто означает традиционное равномерное осреднение. В дальнейшем, в п. показано, что это простейшее преобразование может быть полезным также и в тех случаях, когда нужно определять параметры нескольких составляющих сигнала, и такое, более простое преобразование может рассматриваться, как альтернатива алгоритма Аллана.

Если в () имеется только второе слагаемое (линейный дрейф), то оптимальная весовая функция, определяемая по МНК, имеет вид

W₂(t,τ) = 3t^-3 τ

Отходя от оптимальности, можно использовать кусочно-постоянную функцию, в частности, такую, как (). Таким образом, можно считать, что вариация Аллана исходно приспособлена для определения линейного дрейфа, но дополнена другими преобразованиями, к числу которых относятся: возведение в квадрат, извлечение корня, добавка множителя. Результаты выделения других составляющих при этом становятся побочными продуктами.

Для определения амплитуд синусоидальных составляющих вида x(t)= A sin(ωt+ψ) оптимальным является преобразование типа синхронного детектирования, при котором в параллельных цепях используются линейные преобразования с весовыми функциями в виде

W₁(,τ) = π^-1 sin ωt W₂(t,τ) = π^-1 cos ωt

Вместо них часто используются преобразования с кусочно-постоянными весовыми функциями вида

W₁(,τ) = π^-1 sgn(sin ωt) W₂(t,τ) = π^-1 sgn (cos ωt)

При неизвестной частоте ω алгоритмы оказываются значительно более сложными.

При большом числе детерминированных составляющих выражения для весовых функций становятся громоздкими, и предпочтительным может быть прямое использование МНК в виде вычислительной процедуры многопараметрической минимизации осредненного (равномерно или неравномерно) по времени квадрата невязки по искомым оценкам неизвестных коэффициентов. Однако, отказываясь от оптимизации, можно задавать весовые функции кусочно-постоянными на одинаковых уровнях при изменении знака, подбирая моменты изменения знаков так, чтобы на выходах получались отдельно множители отдельных составляющих независимо от других.