21. Скорректированный коэффициент детерминации

Для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику R2 он обычно заменяется на скорректированный коэффициент детерминации. который даёт штраф за дополнительно включённые факторы, где n - количество наблюдений, а k - количество объясняющих переменных, включая свободный член.

R2ск=R*(2n−k/n−1)

Можно применять при последовательном включении дополнительных факторов с целью уточнения их влияния на выходную зависимую переменную

Основная проблема применения (выборочного)   заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют! Поэтому сравнение моделей с разным количеством факторов с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

Скорректированный (adjusted) 

Для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику   обычно используется скорректированный коэффициент детерминации, в котором используются несмещённые оценки дисперсий:

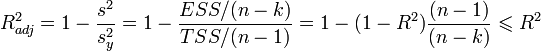
который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество параметров.

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно.

Для моделей с одинаковой зависимой переменной и одинаковым объёмом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии   или стандартной ошибки модели  . Разница только в том, что последние критерии чем меньше, тем лучше.

22. F - тест

F-тест качества спецификации множественной регрессионной модели.

Статистикой обсуждаемого ниже критерия гипотезы H₀: R²=0 (гипотеза о том что модель абсолютно плохая) против альтернативы H₁: 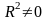служит случайная переменная:

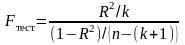(1)

Здесь k — количество регрессоров в модели множественной регрессии, п — объ­ем обучающей выборки (у, X), по которой оценена МНК-модель. В ситуации, когда гипотеза H₀ справедлива, а слу­чайный остаток и в модели обладает нормальным законом распределения, случайная переменная F_тест имеет распределение Фишера с количествами степеней сво­боды ν₁ и ν₂, где ν₁=k и ν₂=n-(k+1) (2)

Данное утверждение положено в основу F-теста. Вот этапы выполнения этой процедуры.

1) вычислить величину (1);

2) задаться уровнем значимости а € (0, 0,05] и при помощи функции FPACПOБP Excel при количествах степеней свободы (2) отыскать (1-α)-квантиль распределения Фишера F_крит

3) проверить справедливость неравенства F<F_крит (3)

Если оно справедливо, то принять гипотезу H₀ и сделать вывод о неудовлетворительном качестве регрессии, т.е. об отсутствии какой-либо объясняющей способности регрессоров в рамках линейной модели.

Напротив, когда неравенство (3) несправедливо —следует от­клонить гипотезу H₀ в пользу альтернативы H₁. Другими словами, сделать вывод о том, что качество регрессии удовлетвори­тельно, т.е. регрессоры в рамках линейной модели обладают способностью объяснять значения эндогенной переменной у.