
- •3. Первый принцип спецификации эконометрических моделей. Типы уравнений в эмм: поведенческие уравнения и тождества (на примере макромодели).
- •4. Типы переменных в экономических моделях. Второй и третий принципы спецификации эконометрических моделей (на примере макромодели). Типы переменных в эконометрических моделях.
- •5. Типы экономических моделей. Спецификация и преобразование к приведённой форме динамических открытых моделей (на примере).
- •6. Структурная и приведённая формы спецификации эконометрических моделей (на примере).
- •7. Отражение в модели влияния на эндогенные переменные неучтённых факторов. Правила включения случайных возмущений (на примере эконометрической модели Самуэльсона-Хикса делового цикла экономики).
- •8. Классическая парная регрессионная модель: спецификация, определение.
- •9. Схема Гаусса-Маркова (на примере модели Оукена: спецификация, экономический смысл переменных и параметров, схема Гаусса-Маркова в виде системы уравненийи в матричном виде).
- •10. Оценка параметров парной регрессии методом наименьших квадратов(суть метода, вывод формул для нахождения оценок коэффициентов через систему нормальных уравнений).
- •11. Матричная форма мнк: спецификация парной регрессионной модели в матричной форме, необходимые условия экстремума в матричном виде, вывод оценки вектора параметров модели.
- •13. Теорема Гаусса - Маркова.
- •15. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели
- •16. Линейная модель множественной регрессии. Порядок ее оценивания мнк в Excel. Смысл выходной статистической информации функции линейн.
- •17. Алгоритм проверки значимости регрессоров во множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки, формулы для расчета статистики.
- •21. Скорректированный коэффициент детерминации
- •23. Алгоритм проверки качества спецификации парной регрессионной модели в Excel (с помощью функции «линейн»).
- •24. Алгоритм проверки адекватности парной регрессионной модели.
- •25. Алгоритм проверки адекватности множественной регрессионной модели (сущность этапов проверки, расчетные формулы, формулировка вывода).
- •27. Процедура интервального прогнозирования по оценённой линейной эконометрической модели значений эндогенной переменной
- •28. Гетероскедастичность случайного возмущения: определение, причины, последствия, количественные характеристики вектора случайных возмущений в условиях гетероскедастичности.
- •29. Алгоритм теста Голдфелда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений в парной регрессионной модели.
- •30. Алгоритм теста Глейзера на наличие или отсутствие гетероскедастичности случайных возмущений.
- •31. Способы корректировки гетероскедастичности. Взвешенный метод наименьших квадратов.
- •32. Способы корректировки гетероскедастичности. Доступный взвешенный метод наименьших квадратов.
- •33. Обобщенная регрессионная модель. Обобщенный метод наименьших квадратов.
- •Оценка параметров обобщенной регрессионной модели
- •34. Автокорреляция случайного возмущения: определение, причины, последствия, количественные характеристики вектора случайных возмущений в условиях автокорреляции.
- •37. Количественные характеристики вектора случайных возмущений в условиях автокорреляции первого порядка (вывод формул).
- •38.Способы корректировки автокорреляции: алгоритм метода Хилдрета-Лу.
- •39.Проблема мультиколлинеарности в моделях множественной регрессии
- •Признаки мультиколлинеарности
- •40. Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарность
- •Последствия частичной мультиколлинеарности
- •45. Алгоритм оценки и проверки адекватности нелинейной по параметрам модели (на примере функции Кобба-Дугласа).
- •46. Фиктивные переменные: определение, назначение, типы.
- •50.Использование фиктивных переменных для определения структурных изменений в экономике.
- •52. Модели временных рядов
- •53. Модели нестационарных временных рядов с трендом и сезонной составляющей и их идентификация.
- •54. Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели; проблема мультиколлинеарности.
- •Проблема мультиколлинеарности.
- •55. Системы одновременных уравнений: проблема оценивания структурных параметров.
- •56. Системы одновременных уравнений: нарушение предпосылки теоремы Гаусса-Маркова о некоррелированности объясняющих переменных и случайных возмущений (на примере макромодели), последствия.
- •58. Идентификация отдельных уравнений системы одновременных уравнений: ранговое условие.
- •60. Косвенный метод наименьших квадратов: алгоритм метода, условия применения.
- •62. Оценка моделей с распределенными лагами с конечным числом лагов.
- •63. Оценка моделей с распределенными лагами с бесконечным числом лагов.
- •64. Оценка моделей с распределенными лагами: метод Алмон
- •65. Тест Дарбина на наличие (отсутствие) автокорреляции вектора возмущений в авторегрессионных моделях.
11. Матричная форма мнк: спецификация парной регрессионной модели в матричной форме, необходимые условия экстремума в матричном виде, вывод оценки вектора параметров модели.


12. Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные статистические процедуры. Требования к наилучшей статистической процедуре: несмещенность и минимальные дисперсии оценок параметров.
Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X (иначе — статистику), с помощью которой судят о значениях параметра a.
Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2.
Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a.
В противном случае оценка называется смещенной.
Если это равенство не выполняется, то оценка ã , полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a , либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки.
Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n.
Так
как для несмещенной оценки M(ã
n
- a)2
есть ее дисперсия
 ,
то эффективность является решающим
свойством, определяющим
качество оценки.
,
то эффективность является решающим
свойством, определяющим
качество оценки.
Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания.
13. Теорема Гаусса - Маркова.
Рассматривается
модель парной регрессии, в которой
наблюдения Y связаны с X следующей
зависимостью: Yi = β1 +
β2Xi
+ εi. На основе n выборочных наблюдений
оценивается уравнение регрессии ![]() .
Теорема Гаусса—Маркова гласит:
Если
данные обладают следующими свойствами:
.
Теорема Гаусса—Маркова гласит:
Если
данные обладают следующими свойствами:
Модель данных правильно специфицирована;
Все Xi детерминированы и не все равны между собой;
Ошибки не носят систематического характера, то есть
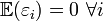 ;
;Дисперсия ошибок одинакова и равна некоторойσ2;
Ошибки независимы, то есть
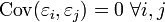 ;
;
—
то
в этих условиях оценки метода
наименьших квадратов эффективны
в классе линейных несмещенных
оценок:
Линейность
оценок показана выражением![]()
Также:
А).
Оценки яв-ся несмещенными, т.е. Eb~=b
и Eâ=a
Док-во:
Введем wt=xt/∑xs2.
При этом ∑wt=0;
∑wtxt=1;
∑wt2 =1/∑xt2;
b~=b+∑wtεt.
Таким образом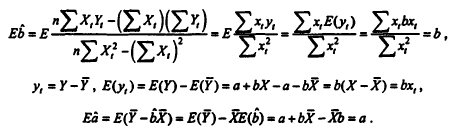 Б).
Оценки являются состоятельными.
Условие
-
Б).
Оценки являются состоятельными.
Условие
- ![]() В
качестве доказательства состоятельности
оценок приведем формулы элементов
ковариационной матрицы вектора b~,
из которых видно, что дисперсии несмещенных
оценок параметров с ростом объема
выборки стрем-ся к 0:
В
качестве доказательства состоятельности
оценок приведем формулы элементов
ковариационной матрицы вектора b~,
из которых видно, что дисперсии несмещенных
оценок параметров с ростом объема
выборки стрем-ся к 0:
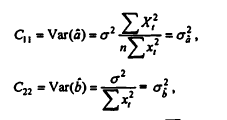 Т.е.
увелечение объема выборки приводит к
устойчивости оценок коэф-в ур-ия.
Считается, что объем выборки должен
удовл-ть соот-ию n>3m-1, где m-кол-во
объясняющих переем-х.
В).
Оценки эфф-ны, т.е. они имеют наименьшую
дисп-ию разброса отн-но теорет-х вел-н
по сравнению с такими же оценками
полученных с примен-м и люб др методов
расчета. Эффективность оценки определяется
критерием вида
Т.е.
увелечение объема выборки приводит к
устойчивости оценок коэф-в ур-ия.
Считается, что объем выборки должен
удовл-ть соот-ию n>3m-1, где m-кол-во
объясняющих переем-х.
В).
Оценки эфф-ны, т.е. они имеют наименьшую
дисп-ию разброса отн-но теорет-х вел-н
по сравнению с такими же оценками
полученных с примен-м и люб др методов
расчета. Эффективность оценки определяется
критерием вида ![]()
Кому не понравилось, смотрим лекцию.
1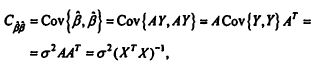 4.
Основные числовые характеристики
вектора оценок параметров классической
множественной регрессионной модели.
Вектор
оценок параметров модели – случайный
вектор, его основными количественными
характеристиками являются: вектор
мат.ожиданий и матрица
автоковариаций.
4.
Основные числовые характеристики
вектора оценок параметров классической
множественной регрессионной модели.
Вектор
оценок параметров модели – случайный
вектор, его основными количественными
характеристиками являются: вектор
мат.ожиданий и матрица
автоковариаций.
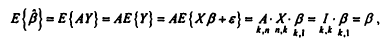 A=(XTX)-1XT
таким
образом, МНК-оценки параметров
множественной регрессии несмещенные.
Построим
матрицу автоковариаций
A=(XTX)-1XT
таким
образом, МНК-оценки параметров
множественной регрессии несмещенные.
Построим
матрицу автоковариаций
,
тк
![]() Доказательство
эффективности несмещенных оценок
b~ выполняется
путем сравнения их дисперсий Var(b^)
с дисперсиями Var(b~)
вектора линейных несмещенных оценок
b~,
определяемого выражением b~ =(A+C)Y,
где С— произвольная (k*n)-матрица. Тогда,
в силу несмещенности оценки b~ и
равенства
Доказательство
эффективности несмещенных оценок
b~ выполняется
путем сравнения их дисперсий Var(b^)
с дисперсиями Var(b~)
вектора линейных несмещенных оценок
b~,
определяемого выражением b~ =(A+C)Y,
где С— произвольная (k*n)-матрица. Тогда,
в силу несмещенности оценки b~ и
равенства ![]() можно
записать:
b=E(b~)=
(A+C)E(Y) = (A+C)Xb = AXb +CXb = b + CXb, откудаследует:
CX=0.
Определим
автоковариационную матрицу вектора
оценок b~:
можно
записать:
b=E(b~)=
(A+C)E(Y) = (A+C)Xb = AXb +CXb = b + CXb, откудаследует:
CX=0.
Определим
автоковариационную матрицу вектора
оценок b~: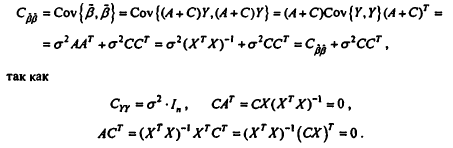 Диагональные
элементы автоковариационных матриц
оценок параметров — их дисперсии.
Диагональные элементы матрицы
ССТ неотрицательны,
поэтому Var(b^)>=Var(b~),
т. е. оценка МНК является эффективной,
имея минимальную дисперсию по сравнению
с любыми несмещенными оценками
неизвестного параметра в классе линейных
процедур.
Диагональные
элементы автоковариационных матриц
оценок параметров — их дисперсии.
Диагональные элементы матрицы
ССТ неотрицательны,
поэтому Var(b^)>=Var(b~),
т. е. оценка МНК является эффективной,
имея минимальную дисперсию по сравнению
с любыми несмещенными оценками
неизвестного параметра в классе линейных
процедур.
