7. Отражение в модели влияния на эндогенные переменные неучтённых факторов. Правила включения случайных возмущений (на примере эконометрической модели Самуэльсона-Хикса делового цикла экономики).

Определение в явном виде эконометрической  модели называется спецификацией эконометрической модели.

Существует 4 принципа спецификации эконометрических моделей:

1. Перевод на математический язык эконометрических утверждений и закономерностей.

2. Число уравнений в модели должно быть равно числу эндогенных переменных. В результате может получиться одно изолированное уравнение или система нескольких уравнений.

3. Датирование переменных

4. Включение в модель случайного возмущения, чтобы показать влияние случайных факторов.

Формы спецификации моделей:

1. Структурная форма модели – эндогенные переменные не выражены явно через предопределенные переменные.

2. Приведенная форма модели – эндогенные переменные представляют собой явно выраженные функции от предопределенных переменных.

В модели Самуэльсона-Хикса экономическим объектом служит закрытая экономика. Ее состояние в текущем периоде t описывается переменными (Y_t, C_t, I_t, G_t). Где Y_t - валовой внутренний продукт (ВВП), C_t - уровень потребления, I_t, - величина инвестиций, G_t – государственные расходы.

При составлении спецификации необходимо учесть следующие экономические утверждения:

1) текущее потребление объясняется уровнем ВВП в предыдущем периоде, возрастая вместе с ним, но с меньшей скоростью;

2) величина инвестиций прямо пропорциональна приросту ВВП за предшествующий период (прирост ВВП за предшествующий период - это разность Y_t-l - Y_t-2);

3) государственные pacхoды возрастают с постоянным темпом роста;

4) текущее значение ВВП есть сумма текущих уровней потребления, инвестиций и государственных расходов (тождество системы национальных счетов).

Перевод на математический язык экономических утверждений данной задачи проводит к спецификации:

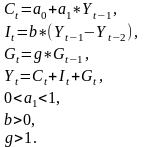(1)

Форма (1) модели близка к приведённой: текущие переменные C_t, I_t и G_t являются явными функциями предопределен­ных переменных, а переменную Y_t очевидно как сделать такой функцией: правые части первых трёх уравнений следу­ет подставить в правую часть четвёртого уравнения. В итоге получится приведённая форма модели Самуэльсона-Хикса:

(2)

Главное отличие эконометрических от других видов моделей является обязательное присутствие случайного возмущения.

Случайное возмущение обладает следующими свойствами:

1. Математическое ожидание случайного возмущения при всех значениях эндогенной переменной равно 0.

2. Гомоскедастичность случайного возмущения – условие постоянности дисперсии случайного возмущения.

8. Классическая парная регрессионная модель: спецификация, определение.

9. Схема Гаусса-Маркова (на примере модели Оукена: спецификация, экономический смысл переменных и параметров, схема Гаусса-Маркова в виде системы уравненийи в матричном виде).

10. Оценка параметров парной регрессии методом наименьших квадратов(суть метода, вывод формул для нахождения оценок коэффициентов через систему нормальных уравнений).

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) ŷ_x минимальна:

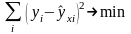(1)

Для того чтобы найти минимум функции (1), надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю. Тогда мы получаем следующую систему нормальных уравнений для оценки параметров a и b

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b:

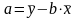
Эта формула получена из первого уравнения системы, если все его члены разделить на n:

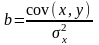
где cov(x,y) — ковариация признаков; σ_х²— дисперсия признака х

Поскольку 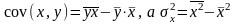, получим сле­дующую формулу расчета оценки параметра b

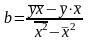
Таким образом явный вид решения системы нормальных уравнений:

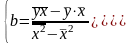
Свойство несмещенности состоит в том, что математиче­ское ожидание оценки должно быть равно истинному значению параметра.

Свойство состоятельности состоит в том, что с увеличе­нием наблюдений дисперсия оценки параметра стремится к ну­лю, т.е. оценка становится более надежной в вероятностном смысле (значения оценки более плотно концентрируются около истинного значения).

Оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с любыми другими оценками этого параметра в классе выбранных процедур.