62. Оценка моделей с распределенными лагами с конечным числом лагов.

Формулировка вопроса:

Оценка моделей с распределенными лагами с конечным числом лагов.

В эконометрике, модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах (иными словами, лаговые переменные).

Спецификацию модели с распределенными лагами с числом лагов k можно записать в следующем виде:

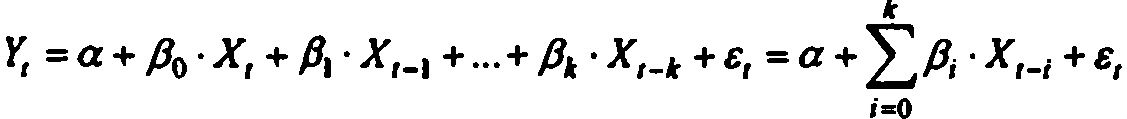
В лаговых моделях параметр β₀ называется краткосрочным мультипликатором, так как он характеризует изменение среднего значения Y под воздействием единичного изменения переменной X, относящейся к тому же моменту времени.

Сумма - 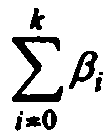долгосрочный мультипликатор, так как она характеризует изменение Y под воздействием единичного изменения переменной Х в каждом из рассматриваемых временных периодов.

При оценке параметров данной модели применяется метод замены переменных:

Таким образом, спецификация представляет собой спецификацию модели множественной регрессии вида:

, параметры которой оцениваются при помощи обычного МНК.

63. Оценка моделей с распределенными лагами с бесконечным числом лагов.

С пецификация модели с бесконечным числом лагов:

Метод геометрической прогрессии

П редполагается, что параметры при лаговых значениях регрессоров убывают в геометрической прогрессии:

Параметр λ характеризует скорость убывания коэффициентов с увеличением лага: чем дальше по времени удалены значения регрессоров, тем меньше их влияние на значение эндогенной переменной в текущий момент времени t.

М одель с учетом данных предположений запишется в виде:

(1)

С пецификацию с бесконечным числом членов можно свести к спецификации с конечным числом при помощи преобразования Койка.

(1)

З апишем данную спецификацию для момента (t-1) и умножим ее на λ:

(2)

( 1)-(2):

И ли

Т аким образом, при помощи преобразования Койка модель с конечным числом лагов сводится к авторегрессионной модели:

Плюс метода: позволяет устранить мультиколлинеарность.

Минусы метода: 1) среди регрессоров появляется лаговая эндогенная переменная, что нарушает одну из предпосылок Гаусса-Маркова;

2) если для случайных возмущений исходной модели ε_t и ε_t-1 справедлива предпосылка о некоррелированности, то для случайного возмущения преобразованной модели будет иметь место автокорреляция.

64. Оценка моделей с распределенными лагами: метод Алмон

Для оценки неизвестных коэффициентов модели с распределённым лагом применяется метод Алмон или лаги Алмон.

Данный метод можно применять к моделям, которые характеризуются полиномиальной структурой лага и конечной величиной лага L:

yt=?0+?1xt+?2xt–1+…+?Lxt–L+?t. (1)

Структура лага определяется графическим методом при отражении зависимости параметров при факторных переменных от величины лага.

Алгоритм метода Алмон реализуется в несколько этапов:

Суть метода Алмон состоит в следующем:

1) зависимость коэффициентов при факторных переменных ?i от величины лага i аппроксимируется полиномиальной функцией:

а) первого порядка ?i=c0+c1*i

б) второго порядка

в) третьего порядка

г) в общем случае полиномиальной функцией порядка P:

Алмон доказал, рассчитать оценки коэффициентов

намного проще, чем найти оценки непосредственно коэффициентов ?i. Подобный метод оценивания коэффициентов ?i  называется полиномиальной аппроксимацией.

2) каждый коэффициент модели (1) можно выразить следующим образом:

?1=c0;

?2=c0+c1+…+cP;

?3=c0+2c1+4c2+…+2PcP;

?4=c0+3c1+9c2+…+3PcP;

…

?L=c0+Lc1+L2c2+…+LPcP.

Подставим полученные выражения для коэффициентов ?i в модель (1):

yt=?0+c0xt+( c0+c1+…+cP)xt–1+…+( ?L=c0+Lc1+L2c2+…+LPcP)xt–L+?t.

3) в полученном выражении перегруппируем слагаемые:

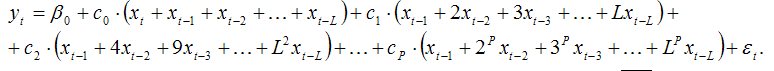
Обозначим слагаемые в скобках при коэффициентах

как новые переменные:

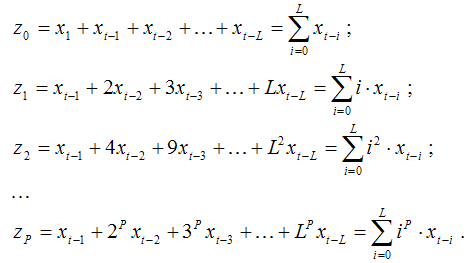
С учётом новых переменных модель примет вид:

yt=?0+c0z0+c1z1+…+cPzP+?t. (2)

4) оценки неизвестных коэффициентов модели (2) можно рассчитать с помощью традиционного метода наименьших квадратов. Далее на основе полученных оценок коэффициентов

5) найдём оценки коэффициентов

модели (1), используя соотношения, полученные на первом шаге.

К основным недостаткам метода Алмон относятся:

1) необходимо заранее знать величину максимального временного лага L, однако на практике это невозможно. Определить величину лага L можно с помощью вычисления показателей тесноты связи, например, линейных парных коэффициентов корреляции, между результативной переменной у и лаговым значением факторной переменной х. Если показатель тесноты связи является значимым, то данную переменную необходимо включить в модель с распределённым лагом. Порядок максимального значимого показателя тесноты связи принимается в качестве максимальной величины лага L;

2) порядок полиномиальной функции Р также заранее неизвестен. При выборе порядка полинома обычно исходят из того, что на практике не используются полиномы более второго порядка, а выбранная степень полинома должна быть на единицу меньше числа экстремумов в структуре лага;

3) если между факторные переменные коррелируют друг с другом, то новые переменные

которые являются линейной комбинацией факторных переменных x, будут также коррелировать между собой. Поэтому проблема мультиколлинеарности в преобразованной модели (2) устранена не полностью. Однако мультиколлинеарность новых переменных zi в меньшей степени отражается на оценках неизвестных коэффициентов ?i исходной модели (1), чем при использовании традиционного метода наименьших квадратов к данной модели. Основным преимуществом метода Алмон является то, что данный метод является универсальным и может быть использован при моделировании процессов, которые характеризуются различными структурами лагов.