55. Системы одновременных уравнений: проблема оценивания структурных параметров.

Для описания сложных эк-х систем, включающих несколько экономических объектов, как правило, используются не отдельные уравнения, а системы. Они могут включать как тождества, так и регресс-еур-я. Отдельные регресс-еур-я системы в качестве предопределенных переменных могут включать как объясняющие переменные, так и объясняемые переменные из других ур-й системы. Поэтому такие системы получили название систем одновременных ур-й. При оценке параметров систем одновременных ур-й приходится сталкиваться с рядом проблем.

Пусть спецификация модели имеет вид: 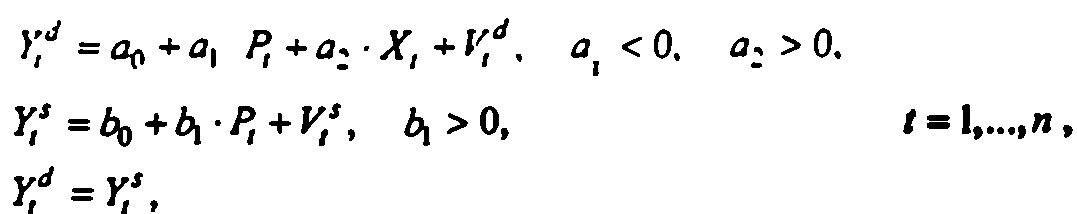где n- объем выборки, — параметры модели. Это структурная форма модели спроса-предложения. Запишем через центрированные значения переменных: 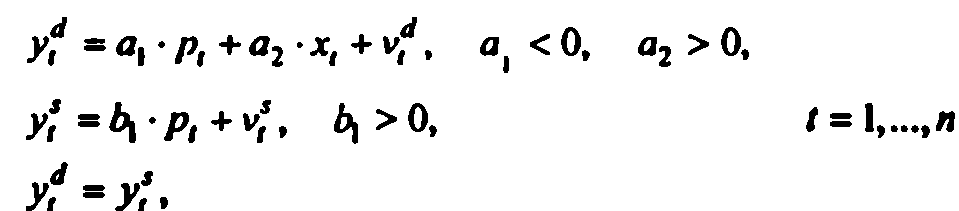Цена р, и величина спроса-предложения у - эндогенные переменными. Предопределенная ее экзогенная переменная — доход х_t. Представим в приведенной форме.

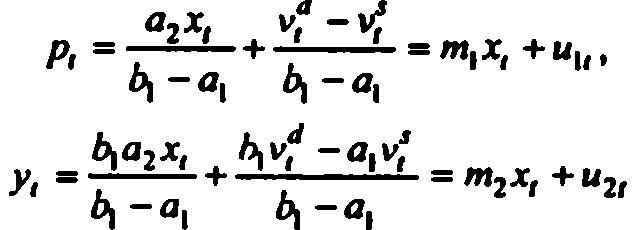
Экзогенные переменные некоррелированы со случайным возмущением, эндогенные имеют ненулевую корреляцию с ними.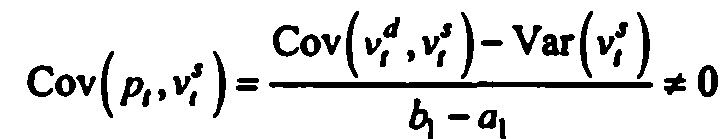 но в моделях со стохастическими регрессорами наличие корреляции между регрессорами и возмущениями приводит к смещенности и несостоятельности МНК-оценок. В приведенной форме регрессор х, некоррелирован с возмущениями, поэтому для оценки параметров приведенной формы применим МНК. Можно попытаться по оценкам приведенной формы вычислить оценки структурной формы. Такой способ оценки наз-ся косвенным методом наименьших квадратов (КМНК). Однако по значениям коэффициентов приведенной формы нельзя сделать никаких выводов относительно структурных параметров первого уравнения. Это связано с так называемой проблемой идентификации. Уравнение для спроса неидентифицируемо.

• Таким образом, при оценке параметров в системах одновременных уравнений приходится сталкиваться со следующими проблемами:

• 1. Одни и те же переменные в одних уравнениях структурной формы являются эндогенными, а в других — предопределенными. Это приводит к корреляции случайных регрессоров с возмущениями данного ур-я и, как следствие, к смещенности и несостоятельности МНК-оцснок его параметров.

• 2. МНК-оценки параметров приведенной формы несмещенные и

• состоятельные, однако они не всегда могут быть использованы для оценки структурных параметров. Возможность определения

• структурных параметров по приведенным связана с так называемой проблемой идентификации. Если такая возможность имеется, то структурная система называется идентифицируемой, в противном случае — неидентифицируемой.

56. Системы одновременных уравнений: нарушение предпосылки теоремы Гаусса-Маркова о некоррелированности объясняющих переменных и случайных возмущений (на примере макромодели), последствия.

МНК позволяет при определенных условиях отыскивать несмещенные и эффективные переменные оценки параметров линейных эконометрических моделей в виде изолированных уравнений, таких как линейная модель множественной регрессии. Одна из предпосылок теоремы Гаусса-Маркова, предпосылка заключается в некоррелированности любой объясняющей переменной модели с любым случайным остатком в уравнениях наблюдений объекта. Если эта предпосылка не выполняется, то МНК-оценки параметров модели теряют при любом конечном объеме n выборки свойство несмещенности. В лучшем случае нарушения предпосылки, а именно: Cov(x_i , u_j) ≠ 0 при i≠j, Cov(x_i, u_j) при i=j. МНК-оценки параметров модели обретают свойство несмещенности в пределе, т.е. при неограниченном увеличении объема выборки n. В худшем случае нарушения предпосылки, а именно: Cov(x_i , u_j) ≠ 0 при i≠j МНК-оценки параметров модели остаются смещенными и при неограниченном увеличении объема выборки. Это значит, что в ситуации МНК-оценки параметров модели оказываются несостоятельными. Корреляция случайных остатков и объясняющих переменных, как правило, присуща поведенческим уравнениям целого класса эконометрических моделей, которые служат наиболее совершенным инструментом изучения изучения экономических объектов.

57. Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие. В общем случае отдельное структурное уравнение системы явля­ется идентифицируемым, если имеется достаточное количество экзогенных переменных, не включенных в само уравнение, которые можно использовать как инструментальные для всех эндогенных объясняющих переменных уравнения. Пусть D — число не включенных в уравнение, но присутству­ющих в системе экзогенных переменных, a G — число включенных в уравнение эндогенных переменных. Уравнение в структурной модели может быть идентифициро­вано, если число не включенных в него экзогенных переменных не меньше числа включенных в него объясняющих эндогенных переменных, т.е. D>G–1 (порядковое условие). Данное условие является необходимым, но не достаточ­ным для идентификации. В частности:

• 
если D = G — 1, то уравнение точно идентифицируемо;

• 
если D> G — 1, то уравнение сверхидентифицируемо;

• 
если D < G — 1, то уравнение неидентифицируемо.