37. Количественные характеристики вектора случайных возмущений в условиях автокорреляции первого порядка (вывод формул).
Зависимость возмущений в различные моменты времени называется автокорреляцией ( сериальной корреляцией). При наличии автокорреляцией между элементами вектора случайных возмущений, его количественные характеристики равны:
, 
,
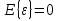
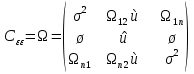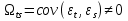где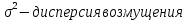
Причины
автокорреляции:
Ошибки
спецификации модели (пропуск важной
объясняющей переменной, использование
ошибочной функциональной зависимости
между переменными и т.д.);
Ошибки
измерений;
Характер
наблюдений (например, данные временных
рядов);
^ Последствия
автокорреляции:
При
наличии автокорреляции
VYRобеспечиваетнесмещенные оценки
параметров, так как первая предпосылка
Гаусса-Маркова выполняется, 
,
но оценка дисперсии возмущения
смешанная: 
.
Это
можно записать так:
.Вектор
остатков e=Mεпри наличии автокорреляции
возмущений имеет следующие основные
количественные характеристики:
E(e)=0, 
. В
этом случае
, что
приводит к нарушению свойства несмещенности
оценки дисперсии возмущения.
Смещенность
оценки дисперсии возмущений приводит
к неадекватным оценкам:
Автоковариационной
матрицы оценок параметров 
;
Границ
доверительных интервалов параметров
модели и значений эндогенной переменной
38.Способы корректировки автокорреляции: алгоритм метода Хилдрета-Лу.
Метод Хилдрета-Лу По данному методу регрессия
оценивается
для каждого возможного значения 
из
интервала [-1;1] с любым шагом (например,
0,001;0,01 и т.д.). Величина 
,
дающая наименьшую стандартную ошибку
регрессии, принимается в качестве оценки
коэффициента
.
И значение 
и 
оценивается
из уравнения регрессии именно с данным
значением
.
39.Проблема мультиколлинеарности в моделях множественной регрессии
Мультиколлинеарность — это понятие, которое используется для описания проблемы, когда нестрогая линейная зависимость между объясняющими переменными приводит к получению ненадежных оценок регрессии. Разумеется, такая зависимость совсем необязательно дает неудовлетворительные оценки. Если все другие условия благоприятствуют, т. е. если число наблюдений и выборочные дисперсии объясняющих переменных велики, а дисперсия случайного члена — мала, то в итоге можно получить вполне хорошие оценки.
Итак, мультиколлинеарность должна вызываться сочетанием нестрогой зависимости и одного (или более) неблагоприятного условия, и это — вопрос степени выраженности явления, а не его вида. Оценка любой регрессии будет страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными. Рассмотрение данной проблемы начинается только тогда, когда это серьезно влияет на результаты оценки регрессии.
Эта проблема является обычной для регрессий временных рядов, т. е. когда данные состоят из ряда наблюдений в течение какого-то периода времени. Если две или более независимые переменные имеют ярко выраженный временной тренд, то они будут тесно коррелированы, и это может привести к мультиколлинеарности.