Оценка параметров обобщенной регрессионной модели

Используется обобщенный МНК, а не обычный.

Обобщенный МНК базируется на Теореме Айткена: В классе линейных несмещенных оценок вектора параметром β обобщенной регрессионной модели оценка

β^{͠ ̽} =A^̽Y=(X^TΩ^-1X)^-1X^TΩ^-1Y является эффективной. Проверим несмещенность оценки Айткена: E{ β^{͠ ̽}}=E(A ^̽ Y)= A ^̽E(Y)= A ^̽Xβ+ A ^̽E(ε)=(X^TΩ^-1X)^-1X^tΩ^-1Xβ+0=β.

В силу третей предпосылки обобщенной регрессионной модели, матрица Ω^-1 положительно определена и симметрична. Существует такая невырожденная n×n матрица P, что

Ω^-1=P^TP.

34. Автокорреляция случайного возмущения: определение, причины, последствия, количественные характеристики вектора случайных возмущений в условиях автокорреляции.

Зависимость возмущений в различные моменты времени называется автокорреляцией ( сериальной корреляцией).

Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость.

Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное.

Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов

Причина:

Ошибки спецификации модели (пропуск важной объясняющей переменной, использование ошибочной функциональной зависимости между переменными и т.д.);

Ошибки измерений;

Характер наблюдений (например, данные временных рядов);

Последствия автокорреляции

При применении МНК обычно выделяются следующие последствия автокорреляции:

1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.

2. Дисперсии оценок являются смещенными. Часто дисперсии, вычисляемые по стандартным формулам, являются заниженными, что влечет за собой увеличение t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.

3. Оценка дисперсии регрессии

S²_e

является смещенной оценкой истинного значения σ² , во многих случаях занижая его.

4. В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

Вектор остатков e=Mε при наличии автокорреляции возмущений имеет следующие основные количественные характеристики:

E(e)=0, . В этом случае, что приводит к нарушению свойства несмещенности оценки дисперсии возмущения.

35. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε_tε_S) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в раз­личные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени на­зывается автокорреляцией (сериальной корреляцией). Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды), ошибка измерений. Для проверки на автокорреляцию используется ряд крите­риев, из которых наиболее широкое применение получил тест Дарбина-Уотсона, основанный на вычислении статистики DW: Последовательность его выполнения: 1.оценка модели и вычисление остатков; 2. вычисление статистики DW: 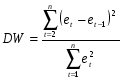3.выбор табличных значений границ критического значения статистики( по параметрам n, k, α):

d_u – верхняя граница критического значения статистика Дарбина-Уотсона

, d_L - нижняя граница критического значения статистика Дарбина-Уотсона 4.определение интервала, в который попадает вычисленное значение статистики DW. При этом возможны следующие случаи:

• Наличие положительной автокорреляции: DW<d_L.

• Наличие отрицательной автокорреляции: DW >4-dL.

• Автокорреляция отсутствует(равна нулю): dU≤ DW≤ 4-dU.

• Зоны неопределенности: dL<dw<dUили 4- dU<dw<4-dL. Поскольку коэффициент корреляции принимает значения -1<=r<=1 то для значений статистики DW выполняется неравенство 0<=DW<=4. Предпосылки теста: случайные возмущения распределены по нормальному закону и гомоскедастичны 36. Способы корректировки автокорреляции (авторегрессионные модели первого порядка).  Автокорреляция случайных возмущений означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. При отрицательной автокорреляции можно видеть, что положительные значения имеют тенденцию следовать за отрицательными и наоборот. При положительной автокорреляции положительные значения чаще следуют за положительными, а отрицательные за отрицательными. При большихρ процесс становится нестационарным, приближаясь к случайному блужданию. С ρ = 0.9 последовательность значений с одним знаком становится длинной, а тенденция возврата к 0 слабой.  Устранение автокорреляции.

1. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1).

Модель парной регрессии:  .Тогда есть два наблюдения: Тогда наблюдениям t и (t-1) соответствуют формулы ,  . Пусть случайные отклонения подвержены воздействию авторегссии первого порядка  Автокорреляция AR(1) может быть устранена в лаговых моделях. Для этого нужно умножить уравнение для y_t-1наρ и вычесть из y_t. Случайный член   (инновация) не является автокоррелированным. Проблема автокорреляции устранена. Однако данный способ приводит к потере первого наблюдения (если мы не обладаем предшествующим ему наблюдением). Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса-Уинстона: ,  . Аналогично устраняется влияние автокорреляции в множественной регрессионной модели.