3.2.4. Энергия упругой волны

Распространение волн связано с переносом энергии. При этом частицы среды не переносятся волной, а совершают колебание около положения равновесия. Скорость колеблющейся частицы, в соответствии с формулами (3.11) и (3.24), равна

.

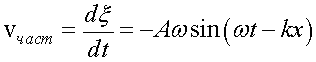Кинетическая энергия частиц, заключенных в объеме , равна (см. формулу (1.29))

.

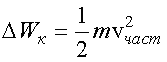Масса выделенного объема m равна

,

где ρ - плотность среды.

Тогда значение кинетической энергии выделенного объема равно

.

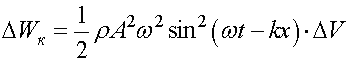Выделенный объем обладает также потенциальной энергией . Можно показать, что

,

где, согласно формуле (3.23), .

Следовательно, кинетическая энергия выделенного объема равна потенциальной энергии.

Полная энергия равна сумме кинетической и потенциальной энергии

.

Полная энергия, возникающая в упругой среде при распространении в ней плоской гармонической волны, равна

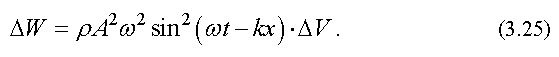
Плотностью энергии называется энергия, заключенная в единице объема, т. е.

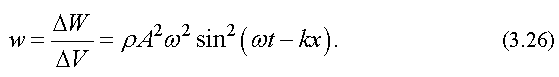
Из формулы (3.26) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. Среднее значение плотности энергии определяется средним значением квадрата синуса

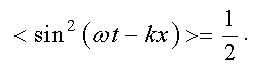
Следовательно, среднее по времени значение плотности энергии в данной точке среды равно

Итак, энергия волны (3.25), плотность энергии (3.26) и ее среднее значение (3.27) пропорциональны плотности среды, квадрату амплитуды и квадрату частоты.

 

3.2.5. Электромагнитные волны

Электромагнитными волнами называется процесс распространения в пространстве переменного электромагнитного поля. Теоретически существование электромагнитных волн предсказано английским ученым Максвеллом в 1865 г., а впервые они экспериментально получены немецким ученым Герцем в 1888 г.

Из теории Максвелла вытекают формулы, описывающие колебания векторов и . Плоская монохроматическая электромагнитная волна, распространяющаяся вдоль оси x, описывается уравнениями

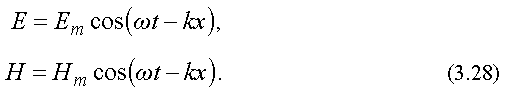
Здесь E и H - мгновенные значения, а E_m и H_m - амплитудные значения напряженности электрического и магнитного полей, ω - круговая частота, k - волновое число. Векторы и колеблются с одинаковой частотой и фазой, взаимно перпендикулярны и, кроме того, перпендикулярны вектору     - скорости распространения волны (рис. 3.7). Т. е. электромагнитные волны поперечны.

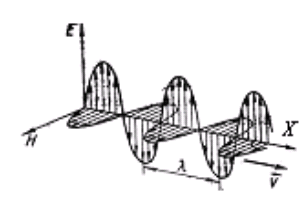
Рис.3.7

В вакууме электромагнитные волны распространяются со скоростью . В среде с диэлектрической проницаемостью ε и магнитной проницаемостью µ скорость распространения электромагнитной волны равна:

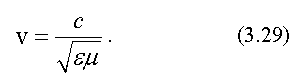
Частота электромагнитных колебаний, так же, как и длина волны, могут быть в принципе любыми. Классификация волн по частоте (или длине волны) называется шкалой электромагнитных волн. Электромагнитные волны делятся на несколько видов.

Радиоволны имеют длину волны от 10³ до 10^-4 м.

Световые волны включают:

• инфракрасное излучение,

• видимый свет в интервале ,

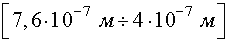• ультрафиолетовое излучение.

Рентгеновское излучение - .

Гамма-излучение   имеет длину волны < 10^-12 м.

 

3.2.6. Световые волны

Световые волны - это электромагнитные волны, которые включают в себя инфракрасную, видимую и ультрафиолетовую части спектра. Длины световых волн в вакууме, соответствующие основным цветам видимого спектра, указаны в нижеприведенной таблице. Длина волны дана в нанометрах, .

Таблица

Цвет	Длина волны, нм	Цвет	Длина волны, нм
красный	760 - 620	голубой	510 - 480
оранжевый	620 - 590	синий	480 - 450
желтый	590 - 575	фиолетовый	450 - 380
зеленый	575 - 510

Для световых волн характерны те же свойства, что и для электромагнитных волн.

1. Световые волны поперечны.

2. В световой волне колеблются вектора и .

Опыт показывает, что все виды воздействий (физиологическое, фотохимическое, фотоэлектрическое и др.) вызываются колебаниями электрического вектора . Его называют световым вектором. Уравнение световой волны имеет сведующий вид

Амплитуду светового вектора E_m часто обозначают буквой A и вместо уравнения (3.30) используют уравнение (3.24).

3. Скорость света в вакууме .

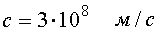Скорость световой волны в среде определяется по формуле (3.29). Но для прозрачных сред (стекло, вода) обычно , поэтому .

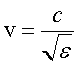Для световых волн вводится понятие - абсолютный показатель преломления.

Абсолютным показателем преломления называется отношение скорости света в вакууме к скорости света в данной среде

Из (3.29), с учетом того, что для прозрачных сред , можно записать равенство .

Для вакуума ε = 1 и n = 1. Для любой физической среды n > 1. Например, для воды n = 1,33, для стекла . Среда с большим показателем преломления называется оптически более плотной. Отношение абсолютных показателей преломления называется относительным показателем преломления:

4. Частота световых волн очень велика. Например, для красного света с длиной волны

.

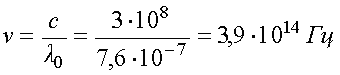При переходе света из одной среды в другую частота света не изменяется, но изменяется скорость и длина волны.

Для вакуума - 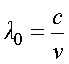; для среды - 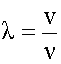, тогда

.

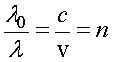Отсюда длина волны света в среде равна отношению длины волны света в вакууме к показателю преломления

5. Поскольку частота световых волн очень велика 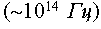, то глаз наблюдателя не различает отдельных колебаний, а воспринимает усредненные потоки энергии. Таким образом вводится понятие интенсивности.

Интенсивностью называется отношение средней энергии, переносимой волной, к промежутку времени и к площади площадки, перпендикулярной направлению распространения волны:

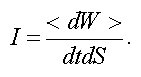
Поскольку энергия волны пропорциональна квадрату амплитуды (см. формулу (3.25)), то интенсивность пропорциональна среднему значению квадрата амплитуды

Характеристикой интенсивности света, учитывающей его способность вызывать зрительные ощущения, является световой поток - Ф.

6. Волновая природа света проявляется, например, в таких явлениях, как интерференция и дифракция.