
- •Сборник заданий
- •«Основы инженерной графики»
- •Перечень графических работ
- •Общие правила оформления индивидуальных заданий (графические работы по дисциплине « Основы инженерной графики»)
- •Графическая работа № 1 «Линии чертежа в соответствии с требованиями стандарта»
- •Методические рекомендации
- •Методические рекомендации
- •Контрольные вопросы
- •Методические рекомендации
- •Проекции призм
- •Проекции пирамид
- •Проекции цилиндров
- •Проекции конусов
- •Аксонометрические проекции
- •Контрольные вопросы
- •Образец выполнения графической работы № 4
- •Задания по вариантам на практическую работу.
- •Задания по вариантам на практическую работу.
- •Задания по вариантам на практическую работу.
- •Графическая работа № 5 «Выполнение чертежа усеченного геометрического тела»
- •Методические рекомендации
- •Контрольные вопросы
- •Методические рекомендации Построение разрезов на чертежах деталей.
- •Построение аксонометрических изображений деталей.
- •Методические рекомендации Составление эскизов деталей изделий с натуры
- •Последовательность действий при выполнении эскизов
- •Эскизирование детали типа штуцер Последовательность изображения детали в проекциях (виды, разрезы, сечения, выносные элементы)
- •Последовательность нанесения размеров на деталь типа штуцер
- •Особенности нанесения параметров шероховатости поверхности
- •Контрольные вопросы
- •Методические рекомендации
- •Выполнения чертежа детали
- •Контрольные вопросы
- •Образец выполнения практической работы № 24
- •Задания по вариантам на практическую работу.
- •Графическая работа № 10
Задания по вариантам на практическую работу.
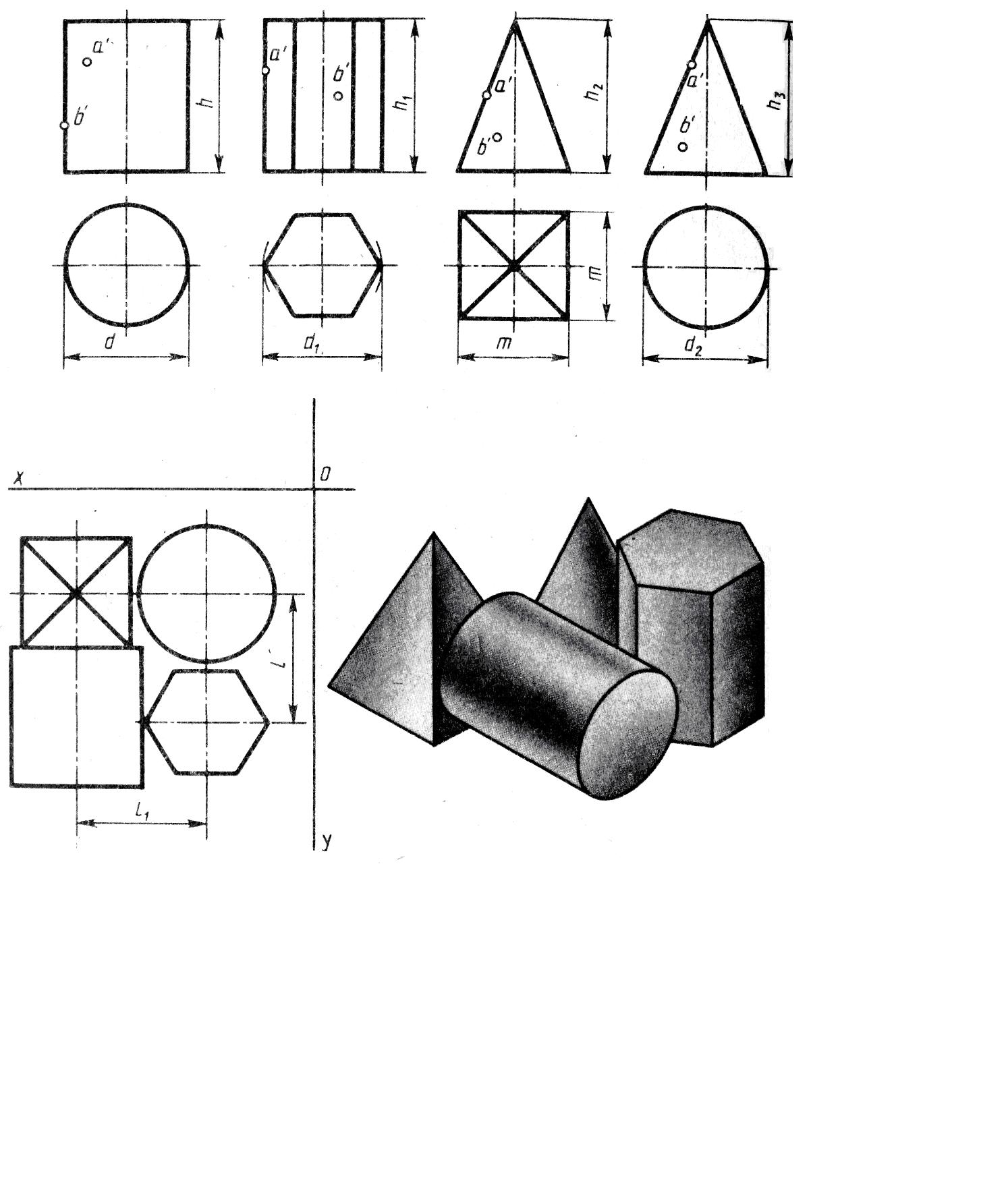
№ варианта |
Размеры, мм |
|||||||||
d |
d1 |
d2 |
m |
h |
h1 |
h2 |
h3 |
l |
l1 |
|
13 |
45 |
45 |
45 |
45 |
50 |
60 |
60 |
70 |
50 |
45 |
14 |
50 |
45 |
45 |
45 |
60 |
70 |
70 |
60 |
55 |
50 |
15 |
50 |
40 |
45 |
36 |
60 |
70 |
50 |
65 |
50 |
50 |
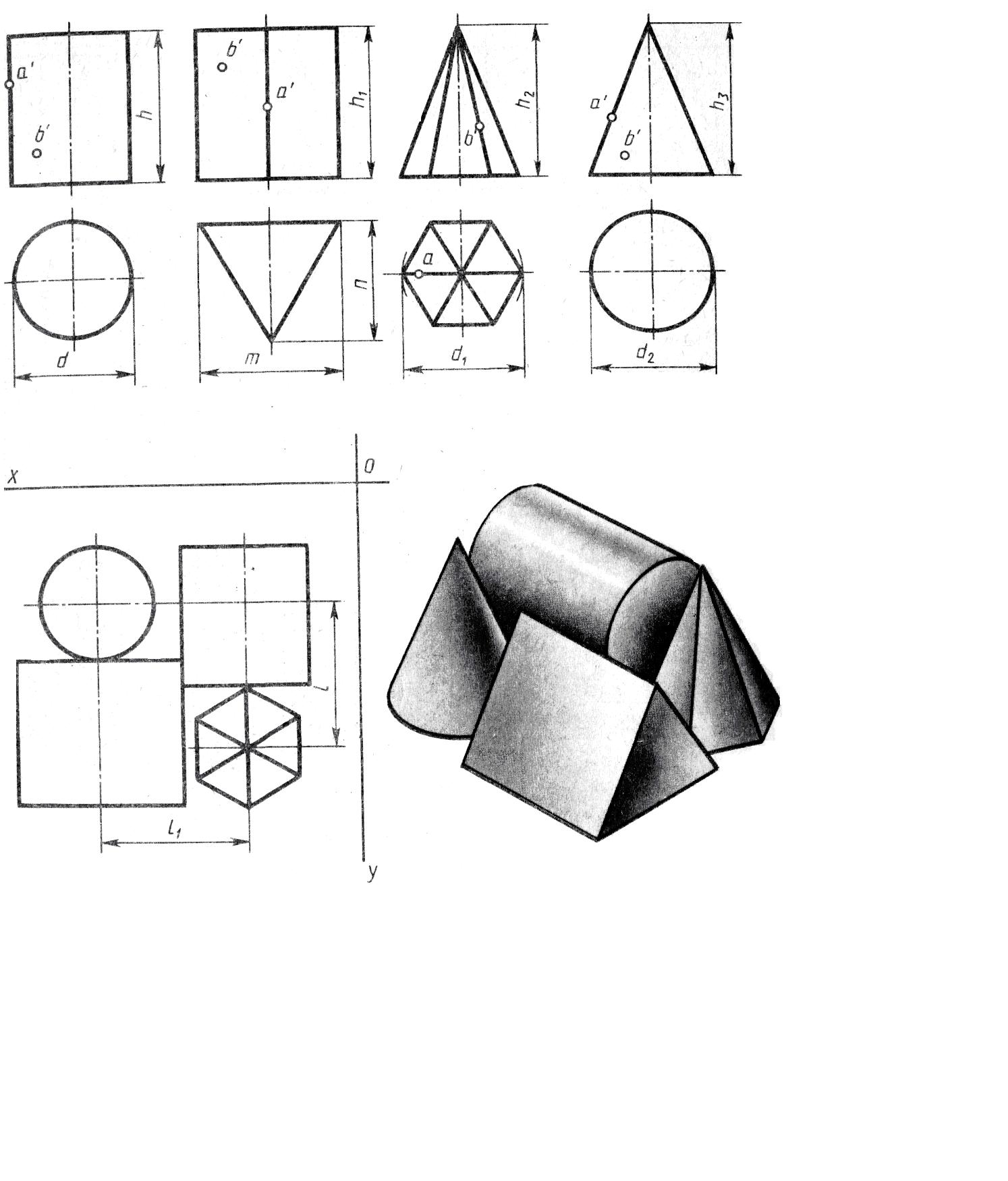
№ варианта |
Размеры, мм |
||||||||||
d |
d1 |
d2 |
m |
n |
h |
h1 |
h2 |
h3 |
l |
l1 |
|
16 |
40 |
40 |
40 |
40 |
50 |
60 |
60 |
70 |
70 |
60 |
40 |
17 |
50 |
40 |
50 |
30 |
40 |
65 |
55 |
60 |
65 |
70 |
50 |
18 |
40 |
50 |
46 |
30 |
45 |
60 |
60 |
65 |
65 |
65 |
43 |
Графическая работа № 5 «Выполнение чертежа усеченного геометрического тела»
Цель: закрепить умение строить проекции геометрических тел на три плоскости проекций, определять проекции точек, принадлежащим поверхностям заданных тел. Закрепить умения по построению аксонометрической проекции и определению действительной величины фигуры сечения различными способами.
Содержание: Выполнить в трех проекциях комплексный чертеж геометрического тела, пересеченного проецирующей плоскостью. Построить в трех проекциях усеченное геометрическое тело, определить натуральную величину фигуры сечения, построить развертку поверхности усеченного многогранника и его аксонометрическую проекцию.
Оформление: Чертеж выполнить на листе чертежной бумаги формата А3, обязательно с рамкой и основной надписью.
Методические рекомендации
Построение пересечения тел плоскостями часто встречается при изображении внешних очертаний деталей машин и приборов, при выявлении внутренних очертаний деталей и во вспомогательных построениях (нахождение точек встречи прямой с поверхностью, отыскание линий пересечения двух поверхностей и др.). При изучении темы нужно обратить особое внимание на построение опорных точек при выполнении сечений и определении действительных величин фигур сечений.
Нужно обратить внимание на то, что при пересечении многогранника плоскостью в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника, а при пересечении тел вращения фигура сечения ограничена плавной кривой линией. Точки этой кривой находят с помощью вспомогательных линий, взятых на поверхности тела (например, образующих конуса и цилиндра). Точки пересечения образующих с секущей плоскостью будут принадлежать кривой линии сечения.
Для того чтобы определить действительную величину сечений, необходимо знать способы преобразования плоскостей проекций: способ вращения и способ перемены плоскостей проекций. В качестве вспомогательных к комплексным чертежам применяют аксонометрические проекции. Это делают в тех случаях, когда нужно дать наглядное изображение предмета. Рассмотрите примеры построения наглядных изображений в изометрической, прямоугольной диметрической и косоугольной диметрической проекциях.
Работать над чертежом нужно в такой последовательности:
начертите рамку и основную надпись, перечертите по своему варианту (таблица 1) две проекции заданного геометрического тела, дочертите третью проекцию;
постройте линии сечения на всех проекциях;
постройте способом перемены плоскостей проекций или способом совмещения действительную фигуру сечения;
вычертите аксонометрическую проекцию;
постройте развертку усеченного тела.
Необходимо помнить, что для построения разверток берется только действительная величина ребер многогранников или образующих тел вращения. 0братите внимание на композицию чертежа; изображения должны быть расположены равномерно без «пустых» или слишком заполненных углов. Чистить чертеж нужно перед обводкой. Удалив все лишние линии, выполните обводку чертежа. Линии построения фигуры сечения сохраните. Заполните основную надпись.
Последовательность построения графической работы рассмотрим на примере усеченной призмы.
Призмой называется многогранник, у которого 2 грани (основания) - равные многоугольники с соответственно параллельными сторонами, а боковые грани – прямоугольники (у прямой призмы) или параллелограммы (у наклонной). Мы рассмотрим прямую призму. Элементы призмы: вершины, ребра (боковые и основания), грани (2 основания и боковые).
Рассмотрим 3 проекции 6-угольной призмы. На главном виде – это прямоугольники, боковые ребра – это горизонтально проецирующие прямые, 6-угольник на виде сверху представляет собой проекцию обоих оснований.
Сечение призмы выполнено фронтально-проецирующей плоскостью.
Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Сечение широко применяется в техническом черчении для выявления формы и внутреннего устройства предметов. В сечении многогранника плоскостью образуется многоугольник. Вершины многоугольника – это точки пересечения ребер многогранника с секущей плоскостью, стороны – это линии пересечения секущей плоскости с гранями многогранника.
Задание на построение комплексного чертежа усеченного многогранника состоит из решения следующих задач:
Построение проекций фигуры сечения.
Определение натуральной величины сечения.
Построение развертки отсеченной части.
Построение аксонометрического изображения отсеченной части.
Рассмотрим все поставленные задачи.
Задача 1. (см. Рис. 1).
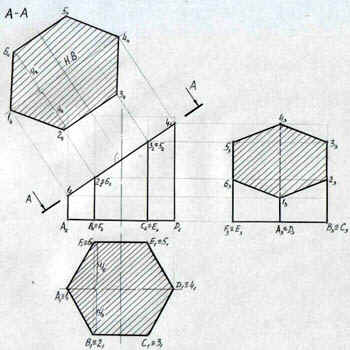 Рисунок
1
Рисунок
1
Для построения трех проекций усеченной призмы выполняем следующие операции:
Строим 3 проекции правильной 6-угольной призмы, сторона основания а = 30, высота - произвольная.
Проводим фронтально-проецирующую секущую плоскость А-А.
На горизонтальной проекции плоскость сечения совпадает с проекцией основания ABCDEF, на профильной проекции сечение строится путем определения профильных проекций точек 1,2,3,4,5,6 и их последовательного соединения.
Задача 2. (см. Рис. 1).
Решение задачи 2 проводится с использованием чертежа, полученного при решении задачи 1. Для определения натуральной величины сечения используем метод вспомогательных секущих плоскостей. Для решения задачи выполняем следующие операции:
На произвольном расстоянии и параллельно секущей плоскости А-А проводим прямую. От фронтальных проекций точек 1, 2, 3, 4, 5, 6 проводим прямые, которые будут перпендикулярны плоскости сечения. Прямые проводим до пересечения с новой плоскостью проекций.
Новые проекции точек 1, 2, 3, 4, 5, 6 получаем перенося горизонтальные проекции данных точек в новую систему координат.
Полученный 6-и угольник в новой системе плоскостей проекций и будет являться натуральной величиной сечения 6-угольной призмы.
Задача 3. (см. Рис. 2).
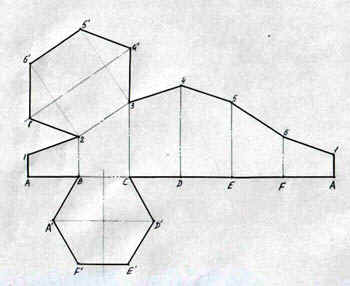 Рисунок
2
Рисунок
2
Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок.
Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией. Построение развертки поверхности многогранника сводится к определению истинной величины каждой его грани по чертежу многогранника (см. Рис. 1). После этого грани многогранника стыкуются (соединяются) по ребрам и вершинам.
Для решения задачи 3 выполняем следующие операции:
Проводим горизонтальную прямую, на которой от произвольно выбранной точки А, откладываем отрезки AB, BC, CD, DE, EF, FA, равные длине стороны основания а = 30.
Из точек A, B, C, D, E, F, A восстанавливаем перпендикуляры и на них откладываем величины ребер усеченной призмы. Величины данных отрезков A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции усеченной призмы. Полученные точки соединяем и получаем развертку боковой поверхности призмы.
К одному из отрезков основания, например к BC, пристраиваем 6-угольник ABCDEF.
К одному из звеньев ломаной, например, к отрезку 2-3, пристраиваем 6-угольник 123456 (сечение призмы), который переносим, используя метод засечек, с рисунка 1.
Задача 4. (см. рис. 3)
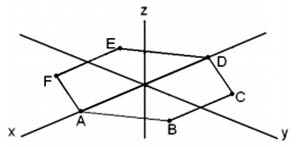
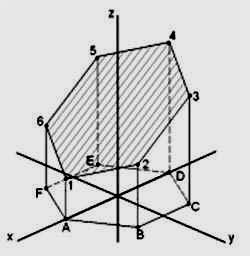 Рисунок 3
Рисунок 3
Строим усеченную 6-и угольную призму в изометрии. Сторона основания призмы, а = 30. Высоты A1, B2, C3, D4, E5, F6 – берем с фронтальной проекции усеченной призмы.
Построение сечения прямого кругового цилиндра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.
Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равномерно расположенных образующих, в данном примере двенадцать. Для этого горизонтальную проекцию основания делят на 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рис. 4, а).
Из комплексного чертежа видно, что плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рис. 4, в).
Фронтальная проекция фигуры сечения совпадает с фронтальным следом Pv плоскости Р. Горизонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра.
Профильная проекция фигуры сечения представляет собой проекцию части эллипса и может быть построена по нескольким точкам, которые строятся с помощью линий связи по горизонтальной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.
Действительный вид фигуры сечения получен на рис. 4, а способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций х1 может быть проведена параллельно следу Pv на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с Pv. От оси х1, откладывают отрезки 5'50=55х, 4'40=44х, т. е. отрезки т, п и т. д., так как расстояние от новой проекции этой точки до новой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекций.
Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения показана на рис. 4, б.
Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную πd, и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку πd, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра Полученные точки 1191 соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой 1191 (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.
Изометрическую проекцию усеченного цилиндра строят следующим образом (рис. 4, в). Сначала строят изометрию нижнего основания (овал) и части верхнего основания — сегмента (часть овала). На диаметре окружности нижнего основания от центра О' откладывают отрезки a, b и т. д., взятые с горизонтальной проекции основания. Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересеченья с осью эллипса.
Через полученные точки проводят прямые, параллельные оси у и на них откладывают отрезки, взятые с действительного вида сечения. Полученные точки соединяют по лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям — овалам.
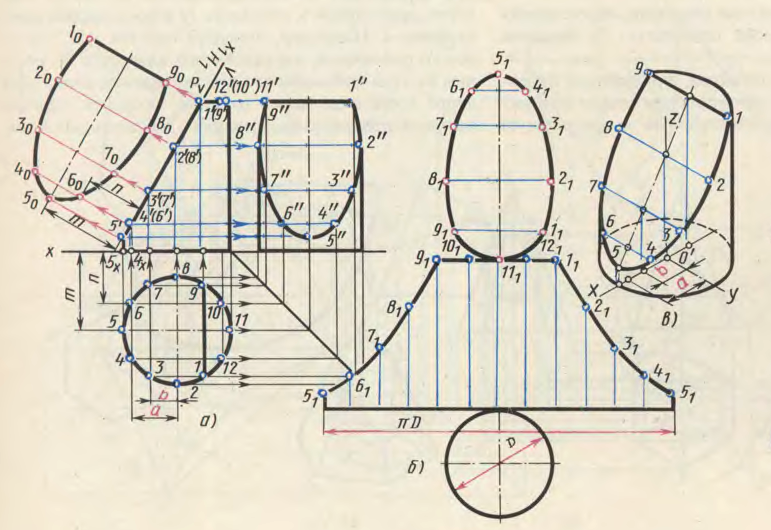
Рисунок 4
