
- •Сборник заданий
- •«Основы инженерной графики»
- •Перечень графических работ
- •Общие правила оформления индивидуальных заданий (графические работы по дисциплине « Основы инженерной графики»)
- •Графическая работа № 1 «Линии чертежа в соответствии с требованиями стандарта»
- •Методические рекомендации
- •Методические рекомендации
- •Контрольные вопросы
- •Методические рекомендации
- •Проекции призм
- •Проекции пирамид
- •Проекции цилиндров
- •Проекции конусов
- •Аксонометрические проекции
- •Контрольные вопросы
- •Образец выполнения графической работы № 4
- •Задания по вариантам на практическую работу.
- •Задания по вариантам на практическую работу.
- •Задания по вариантам на практическую работу.
- •Графическая работа № 5 «Выполнение чертежа усеченного геометрического тела»
- •Методические рекомендации
- •Контрольные вопросы
- •Методические рекомендации Построение разрезов на чертежах деталей.
- •Построение аксонометрических изображений деталей.
- •Методические рекомендации Составление эскизов деталей изделий с натуры
- •Последовательность действий при выполнении эскизов
- •Эскизирование детали типа штуцер Последовательность изображения детали в проекциях (виды, разрезы, сечения, выносные элементы)
- •Последовательность нанесения размеров на деталь типа штуцер
- •Особенности нанесения параметров шероховатости поверхности
- •Контрольные вопросы
- •Методические рекомендации
- •Выполнения чертежа детали
- •Контрольные вопросы
- •Образец выполнения практической работы № 24
- •Задания по вариантам на практическую работу.
- •Графическая работа № 10
Аксонометрические проекции
Для наглядного изображения расположенных в пространстве относительно выбранных плоскостей проекций точек, линий, плоскостей, многогранников и т.д. используются проекции, называемые аксонометрическими (от древнегреческого «аксон» – ось, «метрио» – измеряю) или аксонометрией. Их часто используют для наглядного изображения конструкций приборов, машин на чертеже, особенно на начальных этапах конструирования.
Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, проецируется параллельно на некоторую плоскость, принятую за плоскость аксонометрических проекций.
Изометрическая проекция.
Изометрическую проекцию для упрощения, как правило, выполняют без уменьшения размеров (искажения) по осям x, у, z, т. е. используют приведенный коэффициент искажения, который принимают равным 1. Каждый отрезок, направленный по осям x, у, z или параллельно им, сохраняет свою величину.
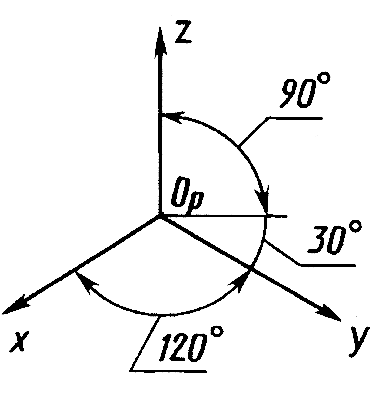
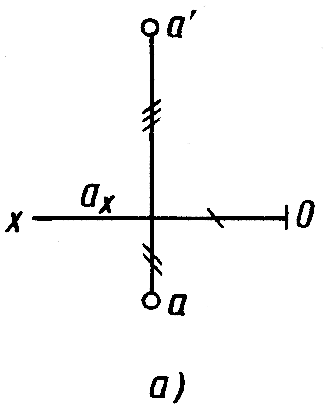
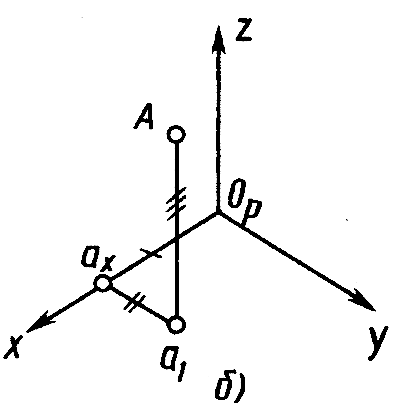
Рис.11.4 Рис.11.5
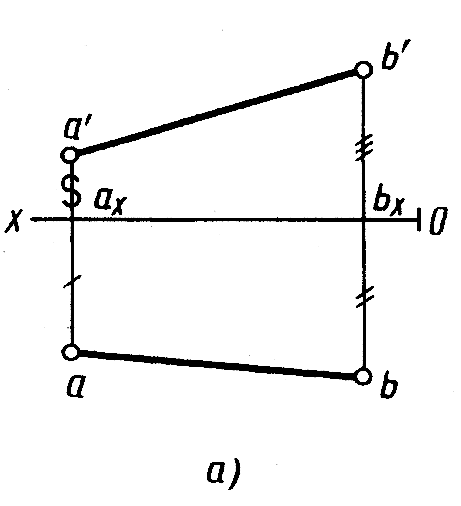
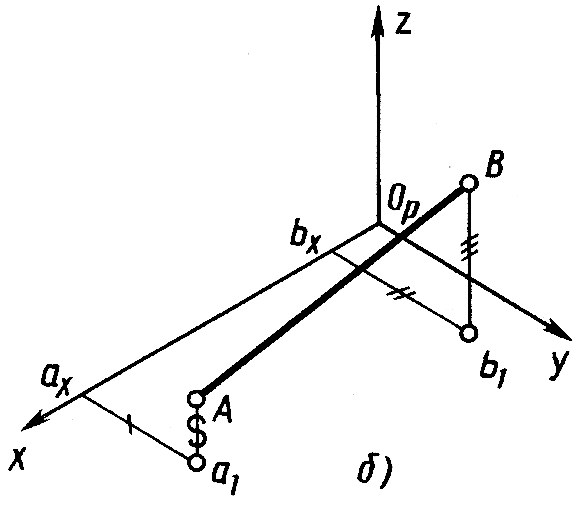
Рис.11.6
Расположение осей изометрической проекции показано на рисунке 11.4. На рисунках 11.5, а, 11.6, а показаны ортогональные, а на рисунках 11.5, б, 11.6, б – изометрические проекции точки А и отрезка AB.
Шестигранная призма в изометрии. Построение шестигранной призмы по данному чертежу в систем ортогональных проекций (слева на рис.11.7) приведено на рисунке 11.7. На изометрической оси z откладывают высоту H, проводят линии, параллельные осям x и у. Отмечают на линии, параллельной оси x, положение точек 1 и 4.
Для построения точки 2 определяют координаты этой точки на чертеже – х2 и у2 – и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.
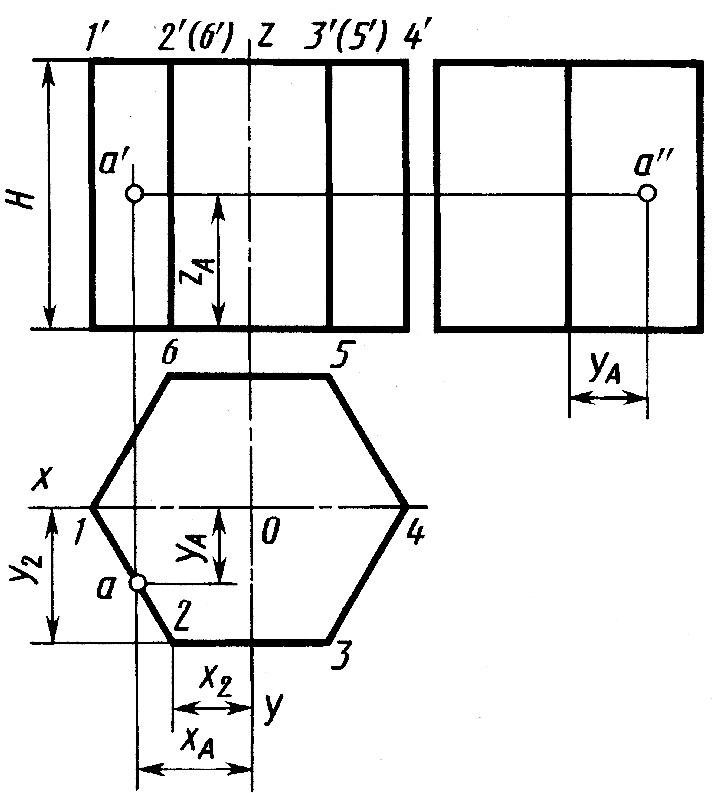
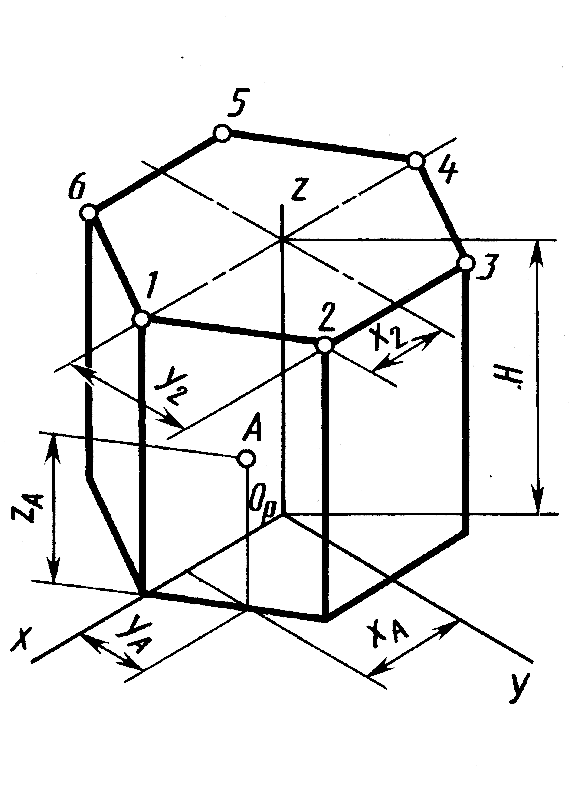
Рис. 11.6 Рис. 11.7
Построенные точки верхнего основания соединяют между собой, проводят ребро из точки 1 до пересечения с осью x, затем – ребра из точек 2, 3, 6. Ребра нижнего основания проводят параллельно ребрам верхнего. Построение точки А, расположенной на боковой грани, по координатам хА (или уА) и zA очевидно из рисунка 11.7
Аксонометрические изображения окружности. Окружности в аксонометрической проекции приведены на рисунке 11.9
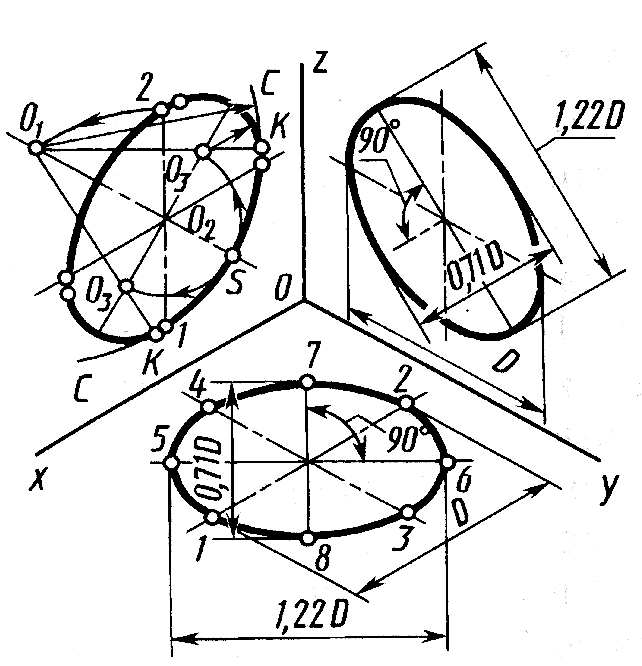 Рис.
11.9
Рис.
11.9
Построение показано на рисунке 11.9 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра делают засечку радиусом R = D на продолжении малой оси эллипса в точке О1 (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки О1 как из центра проводят дуту CSC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О2 как из центра проводят дугу радиуса О2S до пересечения с большой осью эллипса в точках О3. Проводя через точки О1 , О3 прямую, находят в пересечении с дугой CSC точку К, которая определяет О3К – величину радиуса замыкающей дуги овала. Точки К являются также точками сопряжения дуг, составляющих овал.
Аксонометрия цилиндра. Аксонометрические изображения цилиндра определяются аксонометрическими изображениями окружностей его оснований. Построение в изометрии цилиндра высотой H ортогональному чертежу (рис. 11.11 слева) и точки С на его боковой поверхности показано на рисунке 11.11 справа. Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рисунке 11.12. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты x0 y0.
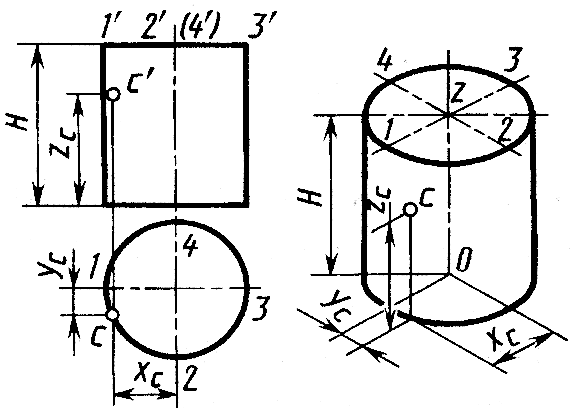
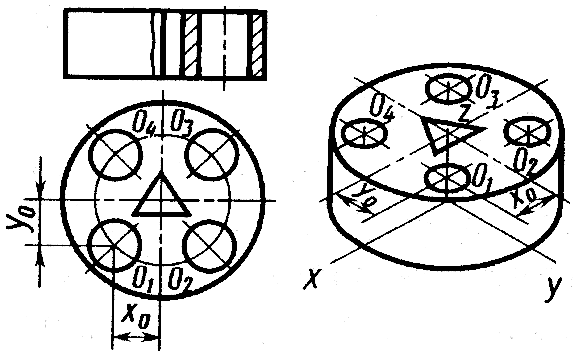
Рис.11.11 Рис.11.12
