Практическое занятие № 7
Тема: «Абсолютная и условная сходимость числовых рядов»
Задача 1.
Исследовать сходимость ряда (определить,
является ли он абсолютно сходящимся,
условно сходящимся, расходящимся)
.
Решение.
Для этого знакочередующегося ряда
выполнены условия признака Лейбница:
1)
2)
.
Следовательно,
указанный ряд сходится. Однако ряд,
составленный из модулей членов данного
ряда, т.е. ряд
расходится (гармонический ряд). Значит
исходный ряд условно сходящийся.
Задание. Исследовать сходимость ряда.
1.
.
Ответ.
Абсолютно сходится.
2.
. Ответ.
Расходится.
3.
.
Ответ.
Условно сходится.
4.
.
Ответ.
Абсолютно сходится.
5.
.
Ответ.
Абсолютно сходится.
6.
.
Ответ.
Абсолютно сходится.
7.
.
Ответ.
Расходится.
8.
.
Ответ.
Расходится.
Практическое занятие № 8
Тема: «Степенные ряды»
Задача 1.
Найти область сходимости ряда
.
Решение.
Имеем
.
Следовательно
ряд сходится при любом значении
.
Задача 2.
Найти область
сходимости ряда
.
Решение. Имеем
. 
.
Исследуем поведение
ряда на концах интервала сходимости
.
При
имеем ряд
,
который расходится (гармонический
ряд). При
имеем ряд
,
который сходится по признаку Лейбница.
Следовательно,
областью сходимости исходного ряда
является полуотрезок
.
Задача
3. Найти
область сходимости cтепенного
ряда
.
Решение. Имеем
. 
.
Следовательно,
ряд сходится при
,
т.е. при
.
При
имеем
ряд
,
который сходится по признаку Лейбница.
При имеем ряд
,
который расходится (гармонический ряд).
Следовательно,
областью сходимости исходного ряда
является полу-отрезок
.
Задание. Найти область сходимости ряда.
1.
.
Ответ.
(-7,
7). 2.
.
Ответ.
[1,
3].
3.
.
Ответ.
[2,
8). 4.
.
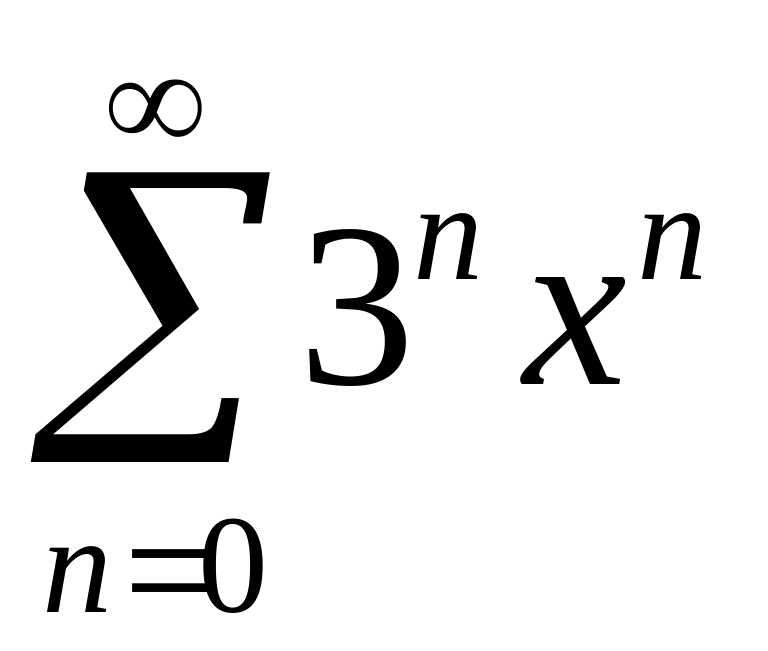Ответ.
.
5.
.
Ответ.
.
Практическое занятие № 9
Тема: «Разложение функций в степенные ряды»
Задача 1.
Разложить
в ряд Маклорена функцию
.
Решение. Найдем значения функции и ее производных при .
………………………………..
Получим :
.
Задача 2.
Выписать
ряд Маклорена функции
.
Решение. В разложении
заменим
на
;
получим:
Задача 3.
Разложить
в ряд Маклорена функцию
.
Решение. Воспользуемся формулой
Так как
,
то заменив
на
,
получим:
где
,
т.е.
.
Задание. Разложить в ряд Маклорена.
1.
.
Ответ.
2.
.
Ответ.
.
3. Разложить
в ряд по
степеням
.
Ответ.
4.
Разложить
в
ряд по степеням
.
Ответ.
.
5. Выписать ряд
Маклорена для функции
.
Ответ.
.
Практическое занятие № 10
Тема: «Некоторые приложения степенных рядов»
Задача 1.
Вычислить
с точностью 0,0001.
Решение. Преобразуем корень
.
Полагаем в разложении
функции
и умножая его на 3 получим
.
Здесь частичная
сумма
обеспечивает заданную точность, т.к.
Задание.
1. Вычислить
с
точностью
0,0001. Ответ.
.
2. Вычислить
с
точностью до 0,001. Ответ.
.
3. Вычислить
с
точностью до 0,0001. Ответ.
.
Задача
2. Вычислить
интеграл
с точностью до 0,001.
Решение.
4. Вычислить
интеграл
с точностью до 0,0001.
Ответ.
5. Вычислить
интеграл
с точностью до 0,001.
Ответ.
