Практическое занятие № 1

Тема: «Двойные интегралы в декартовых координатах»

Задача 1. Перейдя к повторным интегралам, расставить пределы инте­грирования в интеграле , если область D ограничена прямыми .

Решение. Проведем указанные линии и нарисуем область D :

Если взять интеграл по как внешний, а по как внутренний, то переменная х будет меняться от 0 до 2, а у – от функции (линия входа ОА) до функции (линия выхода АВ). Тогда

.

Если же внешний интеграл взять по переменной у, а внутренний – по переменной х, то у будет изменяться от 0 до 2, а х – от функции (линия входа ОВ) до функции (линия выхода АВ). Тогда

.

Ответ. .

Задание. Представить двойной интеграл в виде повторных, предварительно изобразив область D, если D ограничена заданными линиями:

1. . 2.

3. . 4.

Задача 2. Изменить порядок интегрирования в двойном интеграле

.

Решение. Проведя линии , изобразим область D:

Если за внешнюю переменную взять , то будет меняться от 0 до 4, при этом линией входа будет линия ОВ, заданная уравнением , а линией выхода – ломанная О – А – В, причем для линией выхода будет прямая ОА, заданная уравнением , а для линией выхода будет прямая АВ, заданная уравнением .

Таким образом, при изменении порядка интегрирования интеграл разбивается на два интеграла:

.

Ответ. = .

Задание. Изменить порядок интегрирования, предварительно изобразив область интегрирования D:

1. . 2. . 3. . 4. .

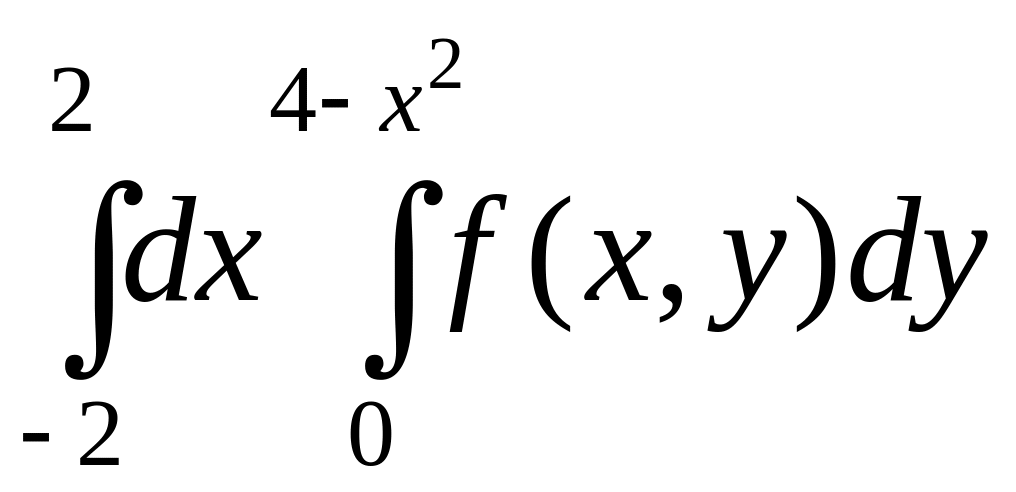Задача 3. Вычислите интеграл , если область D ограничена заданными линиями: .

Решение. Изобразим область D на чертеже и перейдем к повторному интегралу, взяв в качестве внешней переменной переменную х:

.

Задание. Вычислить двойные интегралы

1. , если область D ограничена линиями: . Ответ. -6,4.

2. , Если область d ограничена линиями: . Ответ. .

3. , Если область d ограничена линиями: . Ответ. .

4. , Если область d ограничена линиями: . Ответ. 0. Практическое занятие № 2

Тема 2: «Вычисление тройных интегралов в декартовых координатах»

Задача 1. Вычислить интеграл , если тело V ограничено поверхностями .

Решение. Для данного тела , поэтому

=

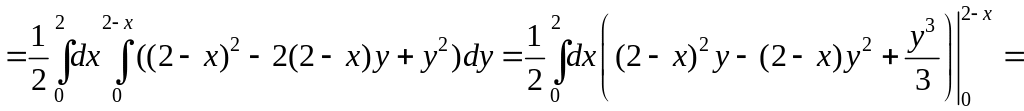
= = Ответ: .

Задание. Вычислить тройные интегралы.

1. , если V - параллелепипед ограниченный плоскостями . Ответ: 24.

2. , если тело V - ограничено плоскостями . Ответ: .

3. , если тело V ограничено поверхностями . Ответ: 12.

4. , если тело V – ограничено поверхностью и плоскос­тями . Ответ: 8.

5. , если тело V ограничено плоскостями . Ответ: .

Практические занятия № 3 – 4

Тема 1: «Вычисление двойного интеграла в полярных координатах»

Задача 1. Перейдя к полярным координатам, вычислить интеграл , если область D задана условиями .

Решение. Область D – верхняя половина круга радиуса 2.

При переходе к полярным координатам угол  будет изменяться от 0 до , а расстояние r- 0 до 2.

Выразим подинтегральную функцию через r и :

.

Тогда

.

Ответ. .

Задание. Перейдя к полярным координатам, вычислить интегралы.

1. , где D – верхнее полукольцо, заданное условиями . Ответ.

2. , где D – часть круга , лежащая в первой четверти. Ответ. .

3. если область D задана условиями . Ответ. 9.

4. , если область D задана условиями . Ответ. 2π.

5. . Ответ. .

6. . Ответ. .

7. . Ответ. .