Лабораторная работа №2

ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ

ПОСРЕДСТВОМ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ

Цель работы: познакомиться с основами проектирования цифровых устройств посредством системы булевых функций; научиться представлять логические функции в совершенной дизъюнктивной форме, совершенной конъюнктивной форме, а также с помощью таблиц истинности

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Элементной базой современных цифровых устройств и систем являются цифровые интегральные схемы. Цифровая интегральная схема (ИС) – это микроэлектронное изделие, изготовленное методами интегральной технологии (чаще полупроводниковой), заключенное в самостоятельный корпус и выполняющее определенную функцию преобразования дискретных (цифровых) сигналов. Номенклатура выпускаемых промышленностью цифровых ИС достаточно обширна и, следовательно, весьма разнообразны реализуемые ими функции преобразования. Простейшие преобразования над цифровыми сигналами осуществляют цифровые ИС, получившие названия логических элементов (ЛЭ).

Для описания работы цифровых ИС, а следовательно и устройств, построенных на их основе, используется математический аппарат алгебры логики или булевой алгебры. Возможность применения булевой алгебры для решения задач анализа и синтеза цифровых устройств обусловлена аналогией понятий и категорий этой алгебры и двоичной системы счисления, которая положена в основу представления преобразуемых устройством сигналов.

Основными понятиями булевой алгебры являются понятия логической переменной и логической функции.

Логической переменной называется величина, которая может принимать одно из двух возможных состояний (значений), одно из которых обозначается символом "0", другое - "1" (для обозначения состояний возможно применение и других символов, например, "Да" и "Нет" и др.). В силу определения логические переменные можно называть также двоичными переменными.

Логической (булевой) функцией называется функция двоичных переменных (аргументов), которая также может принимать одно из двух возможных состояний (значений): "0" или "1". Значение некоторой логической функции п переменных определяется или задается для каждого набора (сочетания) двоичных переменных. Количество возможных различных наборов, которые могут быть составлены из п аргументов, очевидно, равно . При этом, поскольку сама функция на каждом наборе может принимать значение "0" или "1", то общее число возможных функций от п переменных равно .

Таким образом, множество состояний (значений), которые могут принимать как аргументы, так и функции, равно двум. Для этих состояний в булевой алгебре определяются отношение эквивалентности, обозначаемое символом равенства (=) и три операции: а) логического сложения (дизъюнкции), б) логического умножения (конъюнкции), в) логического отрицания (инверсии), обозначаемые соответственно символами: + или – операция дизъюнкции,

или или & – операция конъюнкции,

или – операция инверсии (* – символ аргумента или функции) .

Функция алгебры логики (ФАЛ) представляется в виде:

Y = F (X1, X2, X3, ..., XN).

Данная форма задания ФАЛ называется алгебраической.

Основными операциями или функциями Булевой алгебры являются операция И (конъюнкция), ИЛИ (дизъюнкция) и НЕ (отрицание).

Основные теоремы и законы булевой алгебры Теоремы для одной переменной.

Эти теоремы охватывают все возможные операции над одной переменной X, а также константами 0 и 1.

1. X + 0 = X 5.

2. X + 1 = 1 6.

3. X + X = X 7.

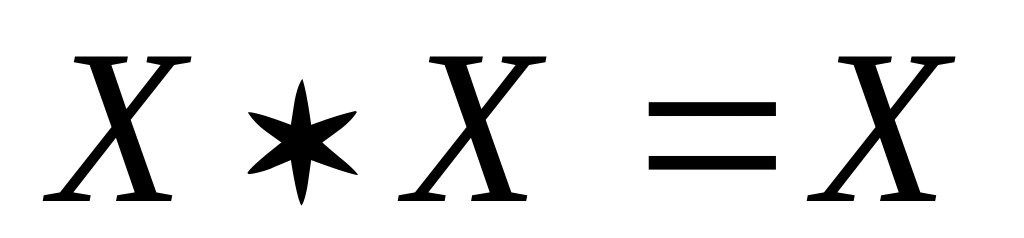
4. 8.

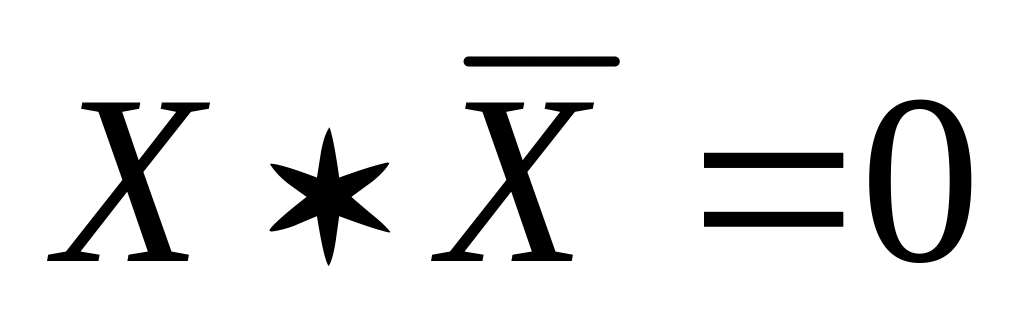
9.

1.2.2. Теоремы и законы для двух и более переменных.

1. Переместительный закон (закон коммутативности): Закон справедлив для любого числа переменных. Он гласит: результат выполнения операции ИЛИ и И не зависит от порядка написания переменных.

Для сложения: 

X+Y=Y+X

Для умножения:

X*Y=Y*X

2. Сочетательный закон (закон ассоциативности). Закон справедлив для любого числа переменных. Он гласит: результат вычислений не зависит от порядка объединения переменных в группы при выполнении операций И или ИЛИ.

Для сложения:

X+Y+Z=X+(Y+Z)=(X+Y)+Z

Для умножения:

X*Y*Z=X*(Y*Z)=(X*Y)*Z

3. Распределительный закон (закон дистрибутивности):

Сложение по отношению к умножению: X+Y*Z=(X+Y)*(X+Z)

(аналогий в обычной алгебре нет)

Умножение по отношению к сложению:

X*(Y+Z)=Х*Y+Х*Z

(можно вносить/выносить общий член в/за скобки)

4. Закон поглощения

Для сложения:  

X+Y*X=X

Х*(1+Y)/1=X*1=X

Для умножения:

X*(X+Y)=X X*X/X+X*Y=X+X*Y=X*(1+Y)=X

Случай 1:

Случай 2:

5. Закон склеивания

Для сложения:

Для умножения:

6. Правило Де-Моргана

Правило Де-Моргана вытекает из принципа двойственности. В соответствии с этим принципом, при замене в логической функции всех аргументов их отрицаниями, и операции умножения/сложения операциями сложения/умножения получается отрицание значения функции. Так, например:

.

Для случая двух аргументов правило Де-Моргана имеет такой вид:

Для сложения:

Для умножения:

Из этого следует, что отрицание значения булевой функции можно получить путем замены всех аргументов их отрицаниями, и всех знаков логического умножения знаками логического сложения и наоборот. Правило Де-Моргана доказывает, что в процессе преобразования булевых функций один и тот же результат может быть получен, как через операции логического сложения, так и через операции логического умножения

Способы представления (задания) функций

Существует четыре основных способа представления булевой функции:

• на словах;

• табличный;

• алгебраический (аналитический);

• числовой

Представление функций на словах.

Этот способ предусматривает словесное описание поведения функции в зависимости от значений аргументов, от которых она зависит.

Например, функция трех переменных (аргументов) принимает значение 1, если два любых аргумента или все три равны 1. Во всех других случаях функция равна 0. Этими предложениями функция полностью определена.