5. Растет погрешности обработки опытно-статистическим методом

Ожидаемая точность обработки может быть определена расчетно-аналитическим методом. Статистический метод оценивает одновременно влияние всех факторов, действующих при обработке детали. К преимуществам статистического метода следует отнести возможность определения точности обработки непосредственно на производстве, без постановки специальных экспериментов. Многократными наблюдениями установлено, что распределение величин погрешности обработки деталей соответствует статистическому закону нормального распределения (Закону Гаусса):

,

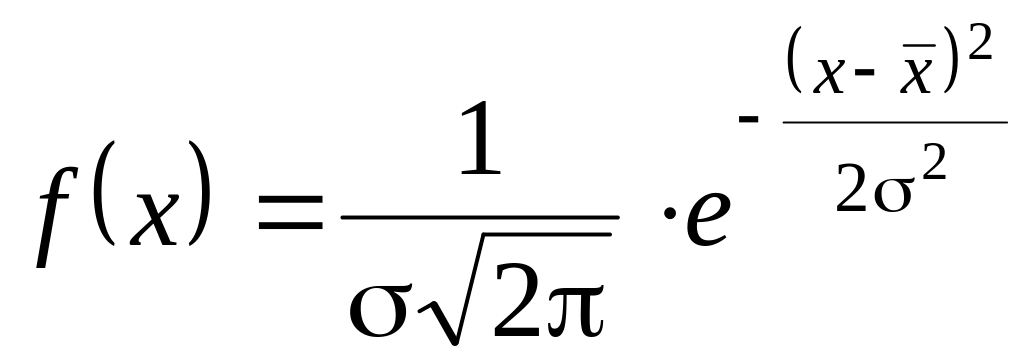где – среднее квадратическое отклонение; – среднее арифметическое отклонение; х – текущее значение размера детали.

При известном поле допуска на размер детали можно довольно точно определить количество годных и бракованных деталей из общего количества :

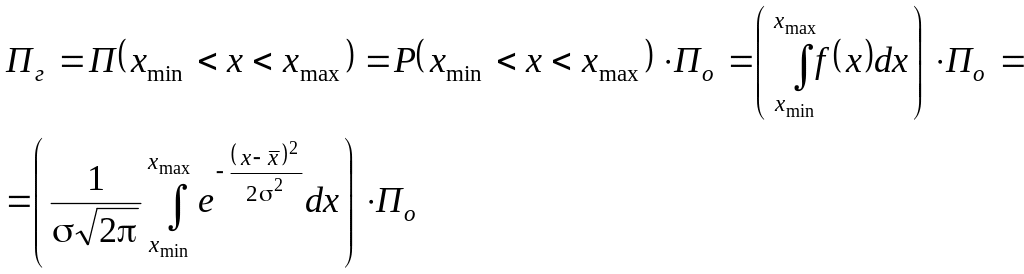
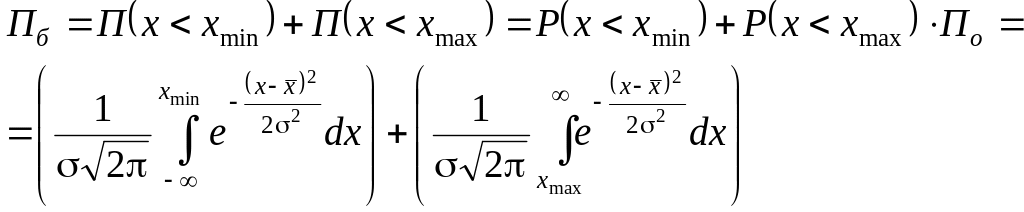
Замена переменных позволяет перейти к табличным значениям функции Лапласа:

,

.

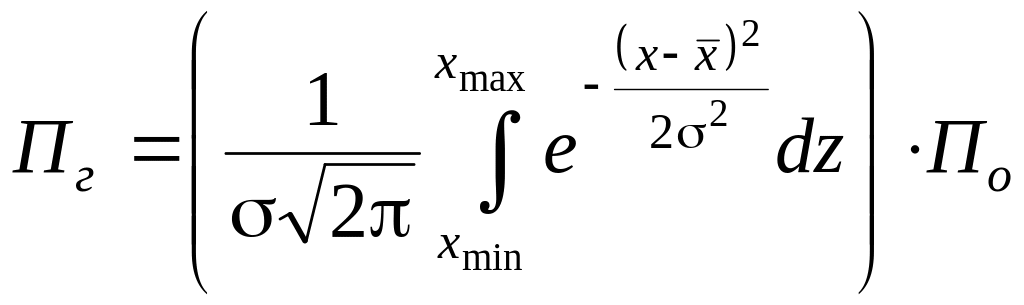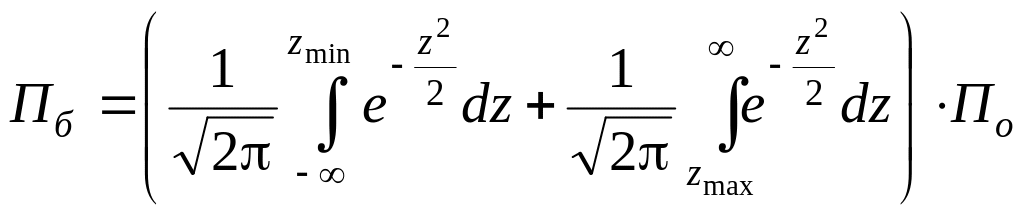Дальнейшее преобразование ведется в зависимости от табличных значений функции Лапласа:

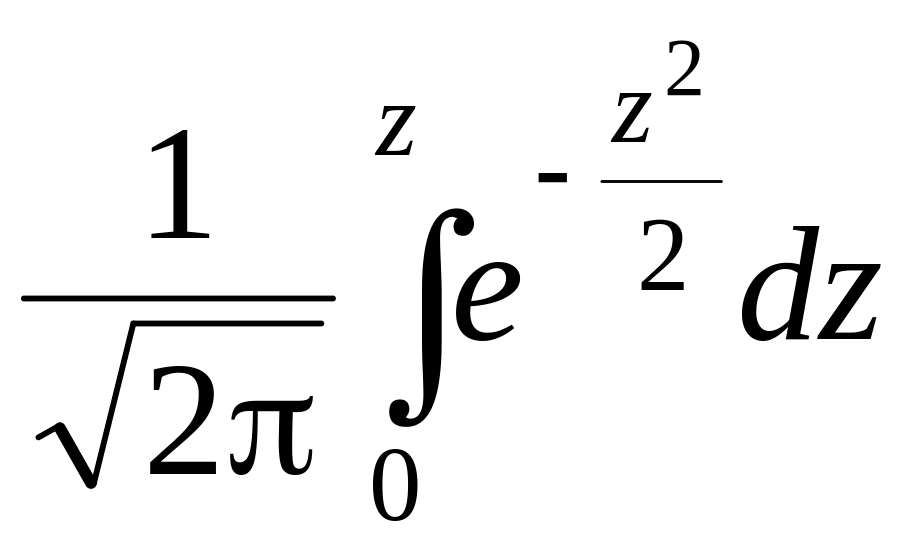или и т.д.

На этом этапе нужно четко понимать, какую площадь под кривой распределения необходимо определить (искомую вероятность) и что нам дает табличное значение функции Лапласа.

Задача. На револьверном станке обрабатывают партию валов = 300 штук диаметром 30_-0,1 мм. По результатам измерения 100 пробных валов величины среднего и среднего квадратического отклонений составляют d = 29,97 мм и = 0,019. Определить число годных и бракованных деталей.

Решение. Количество по нижнему отклонению

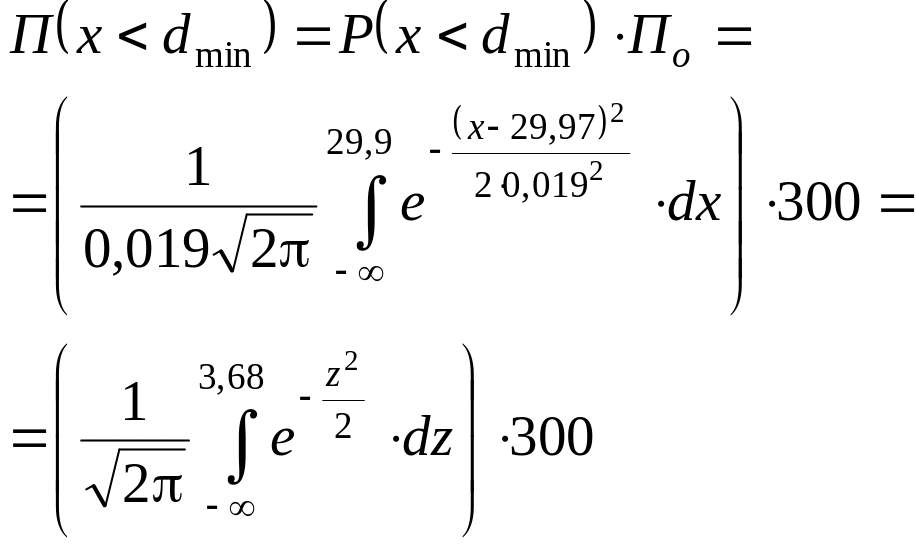
Воспользовавшись (1 или прил. 1 данной работы), получим

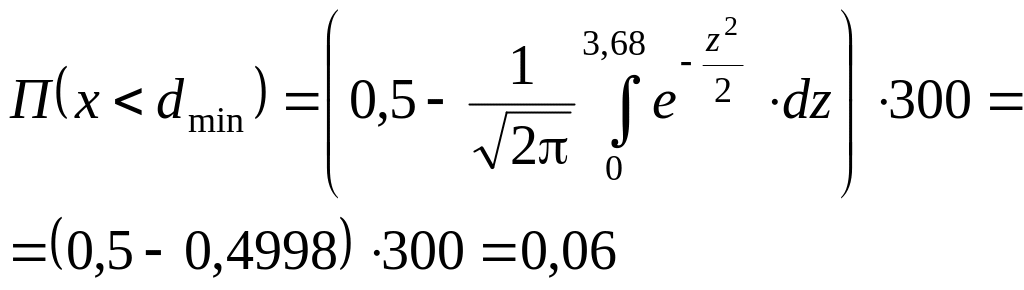
Количество бракованных деталей по верхнему отклонению (исправимый брак)

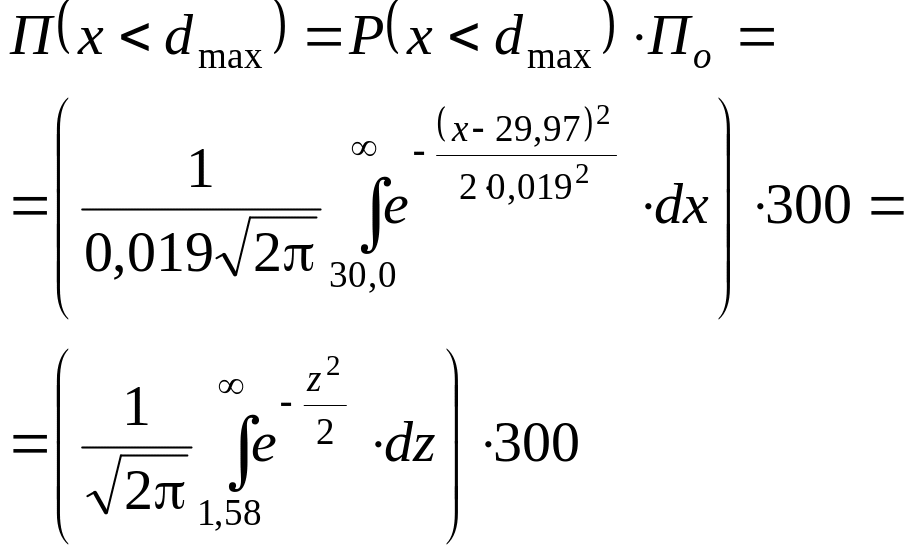
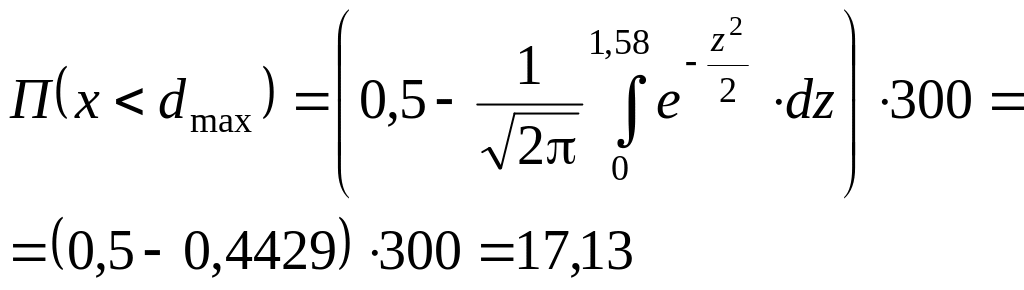
Количество годных деталей

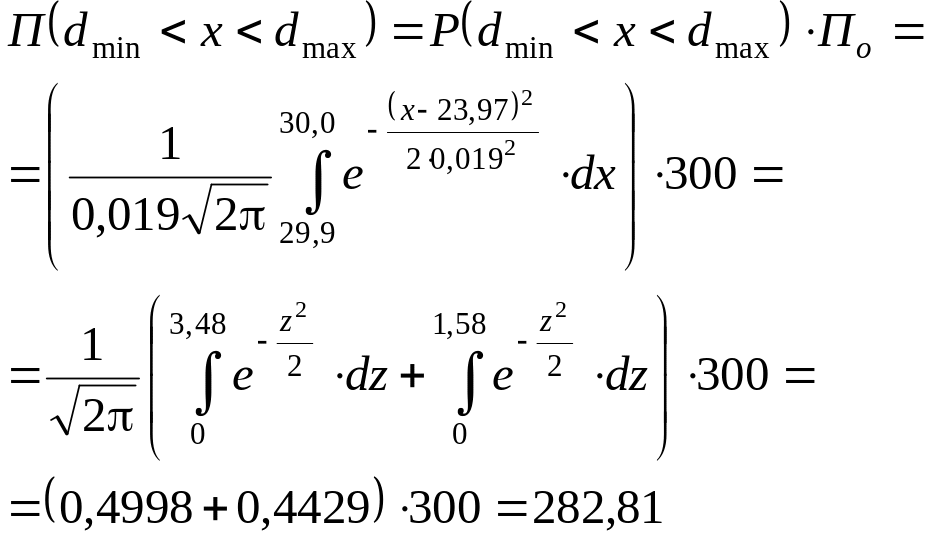
Таким образом, число годных деталей составит 282 шт., а 18 деталей лбудут с исправленным браком.

Варианты заданий

Определить число годных деталей исправимого и неисправимого брака при растачивании отверстий диаметром 130^+0,1 мм из партии 1000 шт. корпусных деталей. Среднее характеристическое отклонение по результатам измерений и величина смещения центра кривой распределения размеров  относительно середины поля допуска представлена в табл. 5.1.

Таблица 5.1

Исходные данные

Вариант	, мм	, мм	Вариант	, мм	, мм
1	2	3	4	5	6
0	0,0167	+0,02	5	0,02	+0,02
1	0,0167	+0,01	6	0,02	+0,01
2	0,0167	0	7	0,02	0
3	0,0167	–0,01	8	0,02	–0,01
4	0,0167	–0,02	9	0,02	–0,02

6. Методы расчета размерных цепей

Существует два метода расчета размерных цепей: по максимальному–минимальному и вероятностный. При 100%-ной взаимозаменяемости размерные цепи рассчитывают по методу максимума–минимума. Если по условиям производства экономически целесообразно назначить более широкие допуски на составляющие звенья (размеры), считая, что возможен выход размеров замыкающих звеньев за пределы поля допуска, то размерные цепи рассчитывают вероятностным методом.

Основное уравнение при расчете размерных цепей при расчете по методу максимума–минимума имеет вид

,

где , – допуски замыкающего и составляющего звеньев; m – число звеньев размерной, включая и замыкающее; – передаточное отношение, в размерных цепях с параллельными звеньями для увеличивающих составляющих звеньев = 1, для уменьшающих – = –1.

При расчете по вероятностному методу

,

где t – коэффициент риска, характеризующий процент выхода расчетных отклонений за пределы допуска; – коэффициент относительного рассеивания, характеризующий закон распределения размеров. Коэффициент риска t определяется принятым процентом риска Р и выбирается из следующего ряда:

Р, %	32	10	4,5	1,0	0,27	0,1	0,01
t	1,0	1,65	2,0	2,57	3,0	3,29	3,89

Коэффициент относительного рассеивания принимается следующим: – если при расчете не известен характер кривой рассеяния размера (мелкосерийное и индивидуальное производство); – если предполагается, что закон распределения кривой рассеяния близок к закону треугольника; – если предполагается, что кривая рассеяния будет иметь нормальный закон распределения (крупносерийное и массовое производство).

При решении прямой задачи, когда по параметрам замыкающего звена требуется найти параметры составляющих звеньев, для упрощения вычисления допусков на составляющие размеры рекомендуется определять среднюю точность по квадрату составляющих звеньев в числах единиц допуска [4] соответственно по методу максимума–минимума и вероятностному методу:

,

,

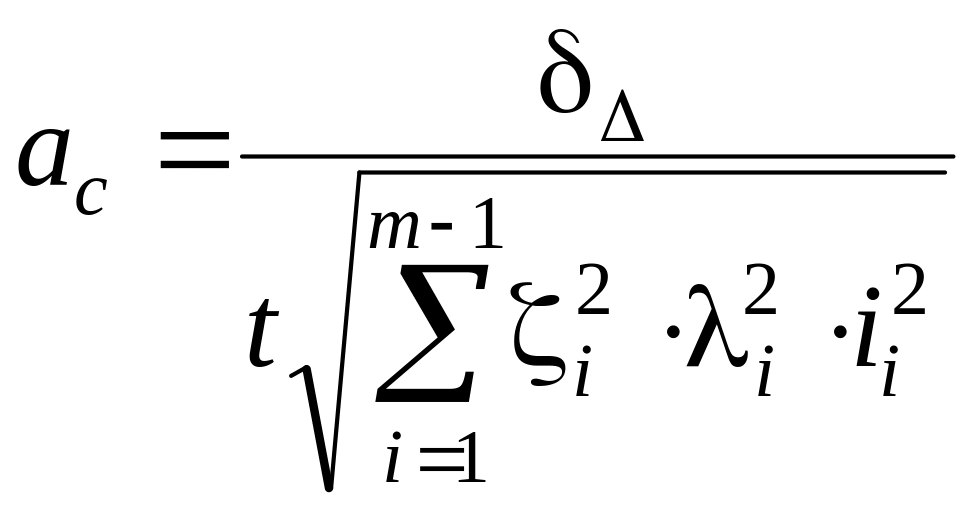где – единица допуска составляющих размеров; считается в мкм. Для размеров до 500 мм [4]

,

где D – размер, для которого определяется величина единичного допуска.

Квалитет точности составляющих звеньев стремятся к тому, чтобы коэффициент запаса был равен или близок к единице:

.

Вполне приемлемым является вариант, когда допуск на составляющие звенья выполняют с точностью по разным квалитетам, учитывая трудность выполнения того или иного размера при обработке.

Координаты середины полей допусков звеньев размерной цепи связаны между собой:

,

где , – координаты середины полей допусков соответственно замыкающего звена и составляющих звеньев.

Предельные отклонения искомого звена

, ,

где и – соответственно верхнее и нижнее отклонения.