- •Интегральное исчисление функции многих переменных
- •§ 1. Определение и свойства двойного интеграла
- •§ 2. Вычисление двойных интегралов в прямоугольной системе координат
- •§ 3. Вычисление двойного интеграла в полярной системе координат
- •3. Вычисление ди в декартовых координатах
- •4. Ди в полярных координатах
- •5. Приложения ди
4. Ди в полярных координатах
Примеры решения
4.1. В повторных интегралах перейти к полярным координатам:
1.

2.
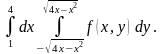
► 1. Пределы
интегрирования позволяют построить
область
 (рис. 10).
(рис. 10).
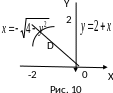
Уравнения границ
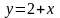 и
и
 в полярных координатах записываются
следующим образом:
в полярных координатах записываются
следующим образом:
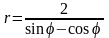 и
и
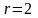 .
.
Угол
меняется от
 до
до
 ,
а
меняется от
,
а
меняется от
 до 2, т.е.
до 2, т.е.
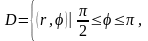
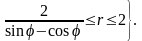 Тогда получаем:
Тогда получаем:

2. Из условия
 следует, что
следует, что
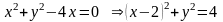 − окружность с центром С
(2, 0) и
− окружность с центром С
(2, 0) и
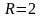 (рис. 11).
(рис. 11).

Уравнение окружности
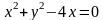 и прямой
и прямой
 в полярных координатах принимает вид:
в полярных координатах принимает вид:
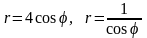 .
.
Решая совместно
уравнения
 ,
находим:
,
находим:
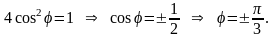
Угол
изменяется от
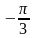 до
до
 .
Любой луч, выходящий из полюса под углом
.
Любой луч, выходящий из полюса под углом
 ,
переcекает
границу области в точках:
,
переcекает
границу области в точках:
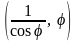 и
и
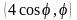 .
Тогда область D
.
Тогда область D

Таким образом,
 ◄
◄
4.2. Переходя к полярным координатам, вычислить ДИ:
1.
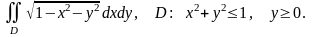
2.

► 1. В данном случае
переход к полярным координатам особенно
удобен, так как область D
− верхняя половина единичного круга
(рис. 12). Для
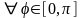 полярный радиус
полярный радиус
 Поэтому, используя формулы (вычисление
ДИ в
полярных координатах), получим:
Поэтому, используя формулы (вычисление
ДИ в
полярных координатах), получим:

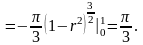

В данном интеграле переход к полярным координатам удобен из-за вида области интегрирования (рис. 13).

Заметим, что
уравнение луча
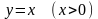 в полярных координатах запишется
в полярных координатах запишется
 ,
а
,
а
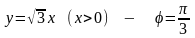 .
Таким образом, используя формулу
(вычисление ДИ
в полярных
координатах), получим:
.
Таким образом, используя формулу
(вычисление ДИ
в полярных
координатах), получим:
 ◄
◄
4.3. Вычислить ДИ
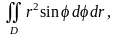 где область D
ограничена линиями
где область D
ограничена линиями
 и лежит вне первой окружности.
и лежит вне первой окружности.
► Сначала определим пределы изменения полярного угла в области D, для чего решаем совместно систему из уравнений линий, ограничивающих область:
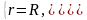

Таким образом,
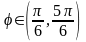 (рис. 14). Полярный радиус r
изменяется в области D
от R
до
(рис. 14). Полярный радиус r
изменяется в области D
от R
до
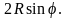

Следовательно,
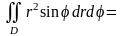
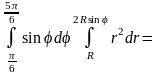
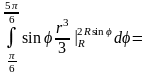

 ◄
◄
Аудиторные задачи
I. В повторных интегралах перейти к полярным координатам:
4.4.
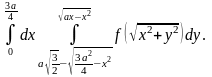
4.5.

4.6.

II. Переходя к полярным координатам, вычислить ДИ :
4.7.
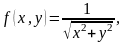 D
− первая четверть круга, радиуса
D
− первая четверть круга, радиуса
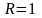 c
центром в т. О
(0, 0).
c
центром в т. О
(0, 0).
4.8.
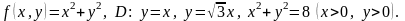
4.9.

4.10.
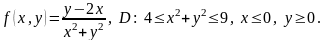
4.11.
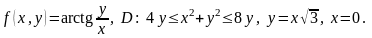
5.2.12.
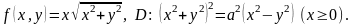
Задание на дом
4.13. В ДИ перейти к полярным координатам и расставить пределы интегрирования:
4.14. Вычислить ДИ:
1.
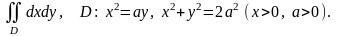
2.
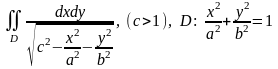
(переход к обобщённой полярной системе координат).
Ответы
4.4.
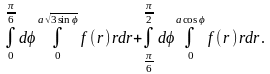
4.5.
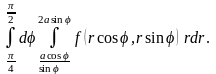
4.6.

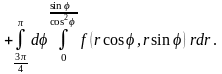
4.7.
4.8.
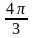
4.9.
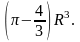
4.10. 3.
4.11.
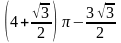
4.12.
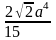
4.13. 1.
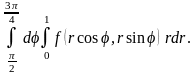
2.
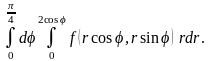
4.14. 1.
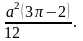
2.

5. Приложения ди
Примеры решения
5.1.
Найти площадь, ограниченную параболами
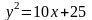 и
и
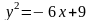 .
.
►
Решая систему уравнений
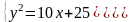 ,
найдем точки пересечения парабол
,
найдем точки пересечения парабол
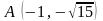 ,
,
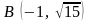 и сделаем чертеж (рис. 14).
и сделаем чертеж (рис. 14).

Область
D
на рис. 14 является правильной относительно
оси OX,
поэтому площадь
 можно представить в виде повторного
интеграла:
можно представить в виде повторного
интеграла:
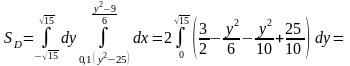
 .
.
Здесь мы воспользовались симметрией области относительно оси OX. ◄
5.2.
Найти площадь, ограниченную кривыми
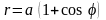 и
и
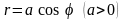 .
.
► В плоскости XOY фигура показана на рис. 15.

Вычислим по формуле (геометрические приложения ДИ) площадь верхней части и удвоим:
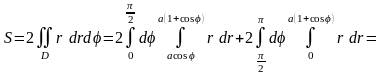

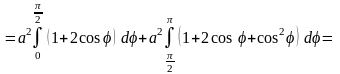
 .
◄
.
◄
5.3. Площади каких областей выражаются интегралами:
1.
 ,
,
2.
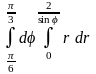 ?
?
►
1. Область ограничена системой неравенств:
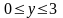 ,
,
 .
Искомая область располагается в полосе
(это сразу отмечается на рисунке).
Уравнения
.
Искомая область располагается в полосе
(это сразу отмечается на рисунке).
Уравнения
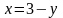 и
и
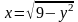 запишем соответственно в виде:
запишем соответственно в виде:
 ,
,
 .
Далее строим область (рис. 16).
.
Далее строим область (рис. 16).


2.
Область ограничена системой неравенств:
 ,
,
 .
.
Луч,
проведенный из полюса через любую
внутреннюю точку области, сразу входит
в область, т.к.
 ,
а точка его выхода находится на линии
,
а точка его выхода находится на линии
 (или
(или
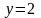 ).
Далее строится область (рис. 17). ◄
).
Далее строится область (рис. 17). ◄
5.3.4.
Найти объем тела, ограниченного
поверхностями:
,
,
 ,
,
 .
.
► Первая поверхность – параболический цилиндр с образующими, параллельными оси OZ (почему)? Сделаем чертеж (рис. 18).

Согласно формуле (геометрические приложения ДИ) получим

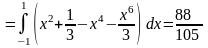 .
◄
.
◄
5.5.
Найти объем тела, ограниченного
плоскостью
и параболоидом
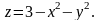
► Сверху данное
тело (рис. 19) ограничено параболоидом
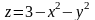 ,
поэтому
,
поэтому
 .
.

Область
D
- круг, его
границу
 получим подстановкой
в уравнение
.
В полярных координатах уравнение этой
окружности имеет вид
получим подстановкой
в уравнение
.
В полярных координатах уравнение этой
окружности имеет вид
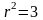 или
или
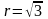 .
Учитывая симметрию тела относительно
плоскостей XOZ
и YOZ,
найдем
.
Учитывая симметрию тела относительно
плоскостей XOZ
и YOZ,
найдем
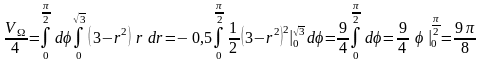 .
.
Откуда
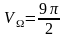 .
◄
.
◄
5.6. Найти массу
квадратной пластинки
 ,
поверхностная плотность которой равна
,
поверхностная плотность которой равна
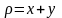 .
.
►
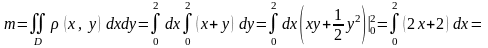
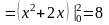 .
◄
.
◄
5.7.
Вычислить площадь части поверхности
параболоида
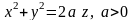 ,
вырезанной цилиндром
,
вырезанной цилиндром
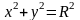 .
.
► Сделаем чертеж
(рис. 20). Согласно
формуле
(геометрические приложения ДИ) получим
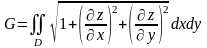 ,
где
,
где
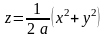 ,
тогда
,
тогда
 .
.

Перейдем к полярным координатам (почему?).
Используя формулу, получим
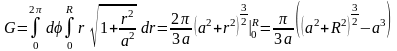 .
◄
.
◄
5.8.
Тонкая пластина имеет форму кругового
кольца с радиусами
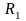 и
и
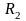
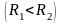 .
Удельная теплоемкость пластинки
меняется по закону
.
Удельная теплоемкость пластинки
меняется по закону
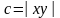 ,
плотность постоянна и равна
,
плотность постоянна и равна
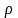 .
Найти количество теплоты
.
Найти количество теплоты
 ,
полученное пластинкой при ее нагревании
от температуры
,
полученное пластинкой при ее нагревании
от температуры
 до
до
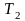 .
.
► Количество теплоты определится по формуле
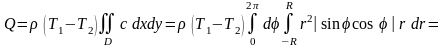
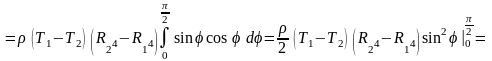
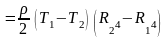 .
◄
.
◄
5.9.
Найти координаты центра масс однородной
пластинки, ограниченной кривыми
 .
.
►
Кривые пересекаются в точках
 и
и
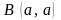 (рис. 21).
(рис. 21).

Поэтому можно записать:
 ,
,

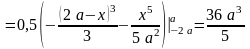 ,
,
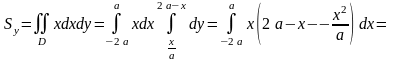
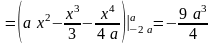 .
.
Подставляя найденные значения в формулы (физические приложения ДИ), имеем:
 ,
,
 .
◄
.
◄
5.10.
Найти моменты инерции однородного
треугольника, заданного уравнениями
 .
.
► Построим область интегрирования (рис. 22).

Используя формулы (физические приложения ДИ), можно записать
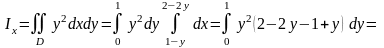
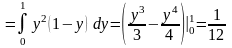 ,
,
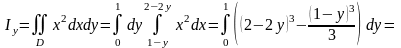
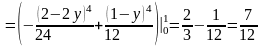 .
◄
.
◄
Аудиторные задачи
I. Найти площадь, ограниченную линиями:
5.11.
 .
.
5.12.
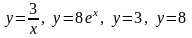 .
.
5.13.
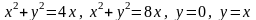 .
.
5.14.
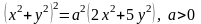 .
.
5.15.
 .
.
5.16.
 (вне кардиоиды).
(вне кардиоиды).
II. Найти объем тела, ограниченного поверхностями:
5.17.
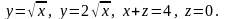
5.18.
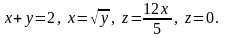
5.19.
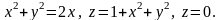
5.20.
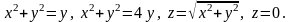
5.21.

5.22.
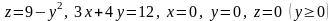 .
.
III.
Найти площадь поверхности
 ,
вырезаемую поверхностями
,
вырезаемую поверхностями
 :
:
5.23.
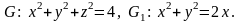
5.24.
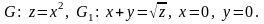
5.25.
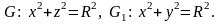
5.26.
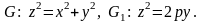
5.27.
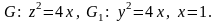
5.28.
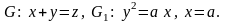
IV. 5.29.
Найти массу круглой пластинки радиуса
 ,
если плотность ее пропорциональна
квадрату расстояния точки от центра и
равна
на краю пластинки.
,
если плотность ее пропорциональна
квадрату расстояния точки от центра и
равна
на краю пластинки.
5.30. Найти массу
пластинки, имеющей форму прямоугольного
треугольника с катетами
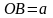 и
и
 ,
если плотность ее в любой точке равна
расстоянию точки от катета
,
если плотность ее в любой точке равна
расстоянию точки от катета
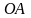 .
.
5.31. Найти массу
квадратной пластинки со стороной
 ,
если плотность материала пластинки
пропорциональна квадрату расстояния
от точки пересечения диагоналей
и на углах квадрата равна единице.
,
если плотность материала пластинки
пропорциональна квадрату расстояния
от точки пересечения диагоналей
и на углах квадрата равна единице.
V. 5.32.
На тонкой пластинке, имеющей форму
параболического сегмента, ограниченного
осью
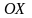 и параболой
и параболой
 ,
распределен электрический заряд с
поверхностной плотностью
,
распределен электрический заряд с
поверхностной плотностью
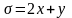 .
Найти полный заряд
.
Найти полный заряд
 .
.
VI. Найти координаты центра масс однородной фигуры, ограниченной кривыми:
5.33.
 .
.
5.34.
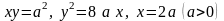 .
.
5.35.
 .
.
VII.
Найти моменты инерции относительно
осей
и
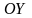 однородной фигуры
однородной фигуры
 ,
ограниченной кривыми:
,
ограниченной кривыми:
5.36.
 .
.
5.37. .
5.38.
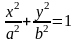 .
.
Задание на дом
5.39. Найти площадь фигуры, ограниченной линиями:
1.
 .
.
2.
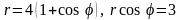 (справа от прямой).
(справа от прямой).
5.40. Найти объем тела, ограниченного поверхностями:
1.
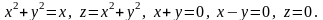
2.
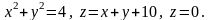
5.41. Найти
площадь части поверхности
 между
между
 и
и
 .
.
5.42. Найти массу пластинки
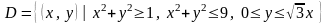 с плотностью
с плотностью
 .
.
5.43. Найти координаты
центра масс однородной фигуры,
ограниченной кривыми
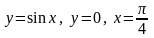 .
.
Ответы
5.11.
 .
.
5.12. 5.
5.13.
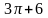 .
.
5.14.
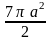 .
.
5.15.
 .
.
5.16.
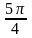 .
.
5.17.
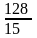 .
.
5.18. 1.
5.19.
 .
.
5.20. 28.
5.21.
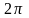 .
.
5.22. 45.
5.23.
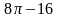 .
.
5.24.
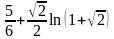 .
.
5.25.
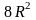 .
.
5.26.
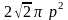 .
.
5.27.
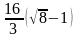 .
.
5.28.
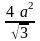 .
.
5.29.
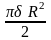 .
.
5.30.
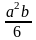 .
.
5.31.
 .
.
5.32.
 .
.
5.33.
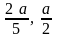 .
.
5.34.

5.35.
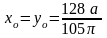 .
.
5.36.
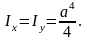
5.37.
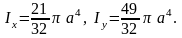
5.38.
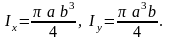
5.39.
1.
 .
2.
.
2.
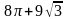 .
.
5.40. 1.
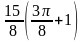 .
2.
.
2.
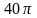 .
.
5.41.
 .
.
5.42.

5.43.
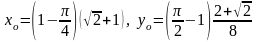 .
.
Вопросы для самопроверки
Каков геометрический смысл теоремы о среднем для ДИ по плоской области от непрерывной неотрицательной функции?
Как записывается неравенствами множество точек области, правильной в направлении а) , б) ?
Какова должна быть область интегрирования, чтобы пределы по x и y были постоянными?
Какая область является правильной в полярной системе координат?
В каких случаях вычисление ДИ целесообразно производить в полярных координатах?