Продовження рисунку 3.24

Задача 10 Побудувати проекції лінії перетину двох поверхонь, одна з яких є круговий конус і фронтально-проекційний циліндр(рис. 3.25).

Розв’язок задачі подано на рис 3.25,а,б,в,г у поетапному розв’язку. Крайні ліва і права твірні конуса перетинаються з поверхнею циліндра у точках 1 і 2. За ними знаходимо 1₁ і 2₁. Точка 1 буде найвищою точкою перетину (рис. 3.25,б) . Найнижчі точки перетину 3 і 4 побудовані за допомогою площини , яка дотикається до найнижчої твірної циліндра (рис. 3.25,б). Точки 5 і 6 розділяють видиму частину горизонтальної проекції лінії перетину від невидимої, визначені за допомогою горизонтальної площини , яка проходить через середину циліндра.

Д ля побудови лінії перетину конуса і циліндра на рис. 3.25,г застосуємо допоміжні горизонтальні січні площини, які перетинають циліндр по прямокутнику, а конус — по колу. У результаті перетину кожного прямокутника відповідним колом одержимо точки лінії перетину поверхонь. З’єднаємо у певній послідовності побудовані точки і дістанемо просторову замкнену криву лінію перетину цих поверхонь. Невидима частина горизонтальної проекції лінії перетину зображена штриховою лінією.

а)

б)

в)

Рисунок 3.25

г)

Продовження рисунку 3.25

Задача 11 Побудувати проекції лінії перетину конуса та кулі (рис. 3.26).

Для побудови точок перетину цієї лінії також вибираємо допоміжні горизонтальні площини, які перетинають обидві поверхні по колах. Ці кола на горизонтальну площину проекцій проектуються у кола.

.

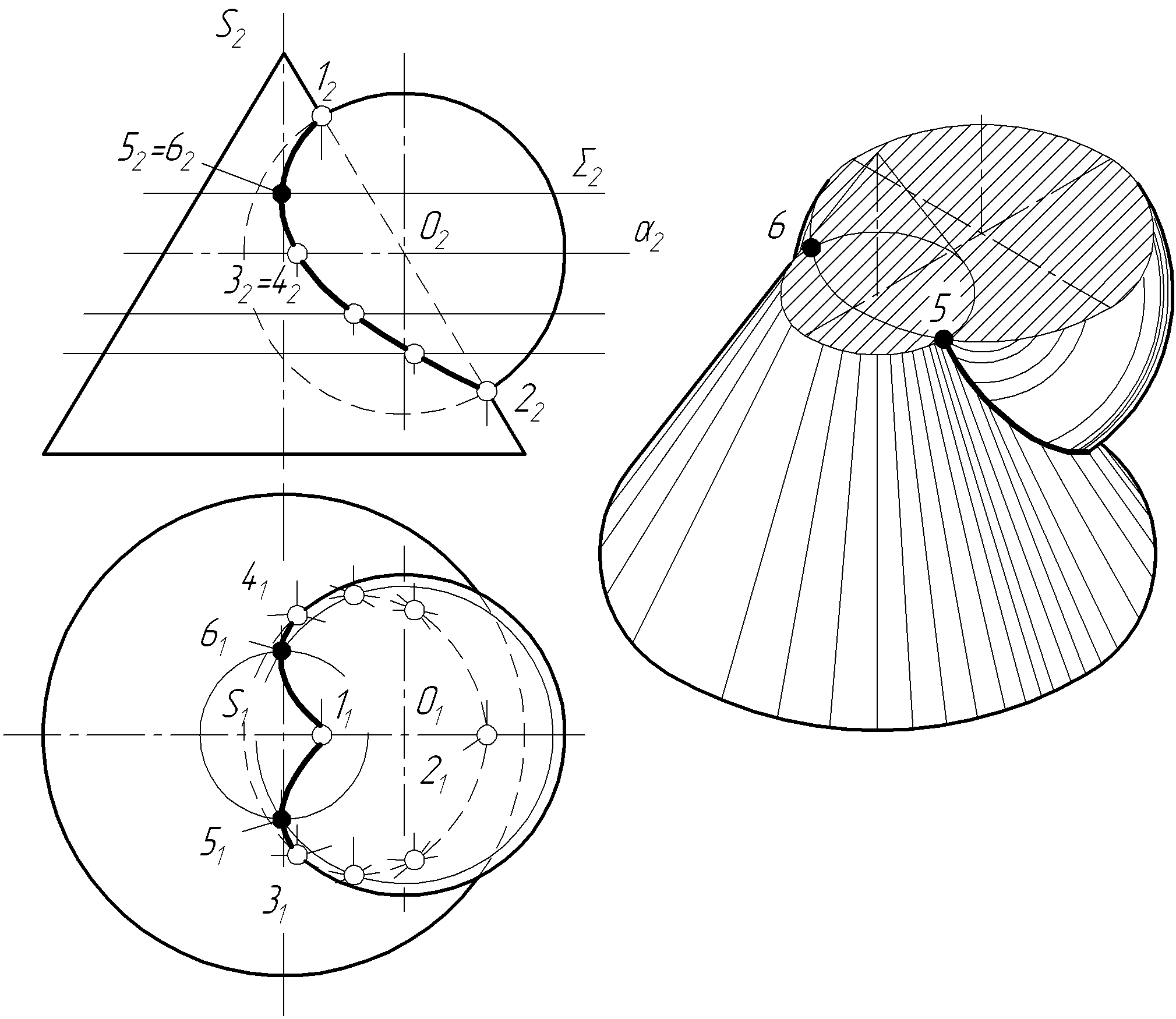
Рисунок 3.26

Спочатку, як і у попередніх задачах, знайдемо характерні точки. Точки 1 і 2 розташовані на перетині очеркових ліній фронтальної проекції і знаходяться у площині спільної симетрії поверхонь. Точки 3 і 4 знаходяться на екваторі кулі, знаходимо їх за допомогою площини , яка перетинає кулю по екватору, а конічну поверхню — за відповідним колом. Горизонтальні проекції цих кіл перетинаються в точці 3₁ і 4₁. Вони лежать на лінії одного проекційного зв’язку до p₂, тому на фронтальній площині проекцій співпадають. Решту проміжних точок знаходимо за аналогією за допомогою горизонтальних площин.

На фронтальній площині проекцій не завжди побудована крива видима (невидима її частина закривається видимою), половина її знаходиться на заданій стороні даних поверхонь. На горизонтальній проекції видима частина кривої відділяється від невидимої точками 3 і 4, що лежать на екваторі

Задача 12 Побудувати проекції лінії перетину циліндра з півкулею (рис. 3.27).

Насамперед знайдемо характерні точки:

а) у точках 3 і 4 крайні ліва і права твірні циліндра перетинаються з поверхнею кулі. Щоб знайти ці точки, застосуємо фронтальну площину , яка проходить через середину циліндра і перетинає кулю по колу, а циліндр по твірних;

б) у точках 9 і 10 головний меридіан кулі перетинає твірні циліндра;

в) найближча точка 5 і найвіддаленіша від спостерігача точка визначається за допомогою січних площин  і . Проміжні точки лінії перетину знаходимо за допомогою допоміжних фронтальних площин. Так площина  перетинає поверхню кулі по колу, а поверхню циліндра – по твірних. На перетині цих ліній знаходимо точки 7 і 8 (рис. 3.27).

Найвищу і найнижчу точки перетину лежать на горизонтально-проекційній площині , що проходить через вісь циліндра і центр кулі. З’єднавши всі отримані точки лінії перетину у певній послідовності, дістанемо шукану лінію перетину.

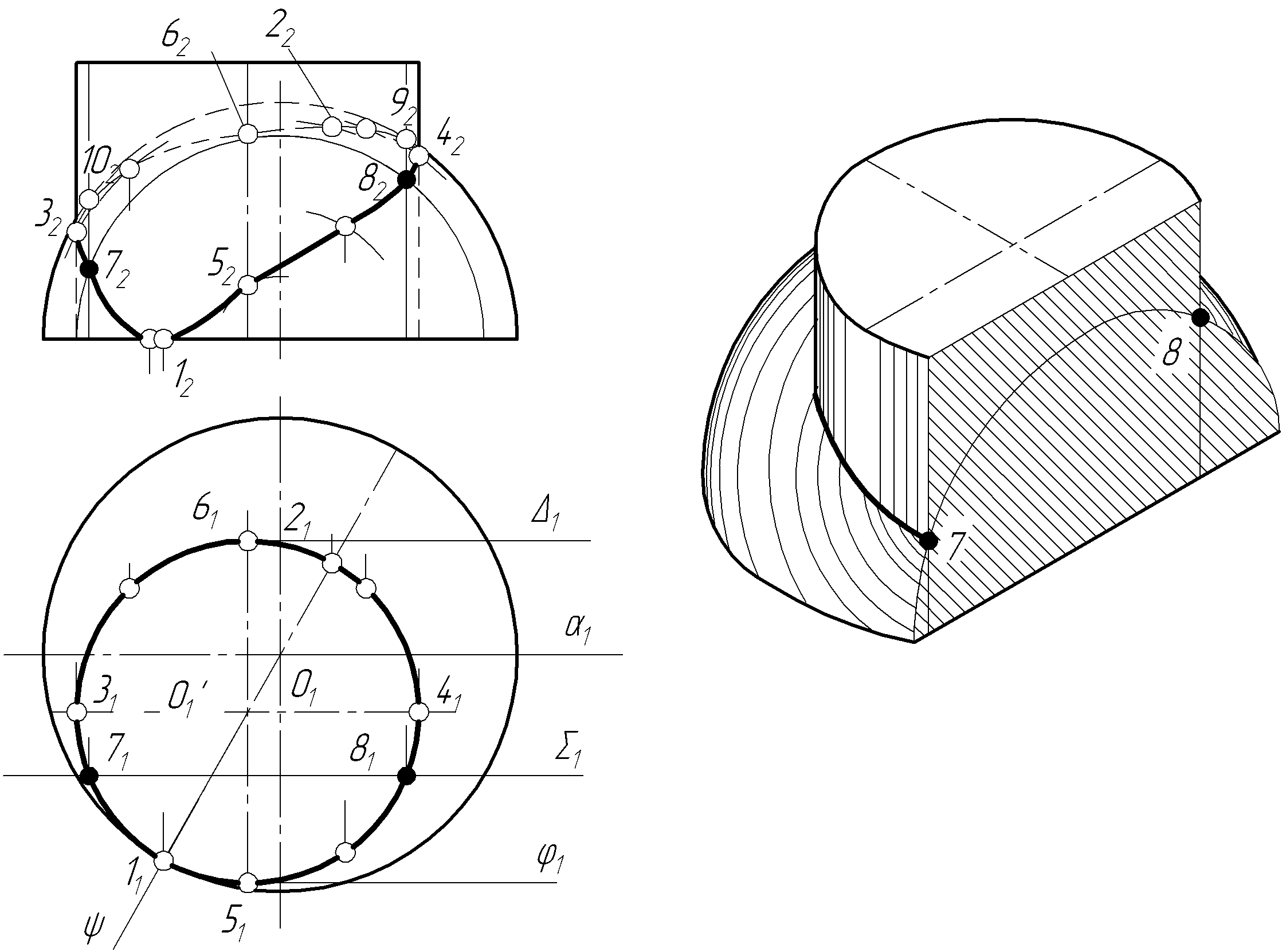
Рисунок 3.27

Задача13 Побудувати проекції лінії перетину двох конусів методом січних сфер (рис. 3.28).

Перетинаються два конуси обертання, осі яких розміщені в площині, яка є паралельною до площини p₂. Для пошуку точок, які належать лінії перетину, використаємо допоміжні січні сфери, центри яких лежать на перетині осей конусів (точка1О) і кожна із сфер перетинає задані конуси по колах. Проекції кіл, по яких сфера радіусу r перетинає обидва конуси — відрізки прямої.

Характерними точками в даному випадку є точки, які лежать на перетині двох конусів. Це точки 1, 2, 3, 4.

Найменшою сферою буде сфера, яка є вписана в один із конусів і перетинає другий конус. Проводимо коло з центру О₂ взявши його за проекцію кулі. Будуємо проекції кіл, по яких ця куля перетинається з одним із конусів – в, с і дотична до другого конуса, тому перетне по колу а. На перетині цих відрізків дістанемо точки 5₂6₂ і 7₂8₂.

Характерні точки 9, 10, 11, 12 знаходимо як точки перетину найближчої і найдальшої твірної конуса з колом, яке одержали від перерізу конуса горизонтальною площиною, проведеною через точку О. Спочатку знаходимо 9₁, 10₁, 11₁, 12₁, а за ними 9₂,110₂, 11₂, 12₂. Для визначення проміжних точок, що належать лінії перетину, проводимо ще ряд січних сфер різними радіусами, але більшими ніж r_min.

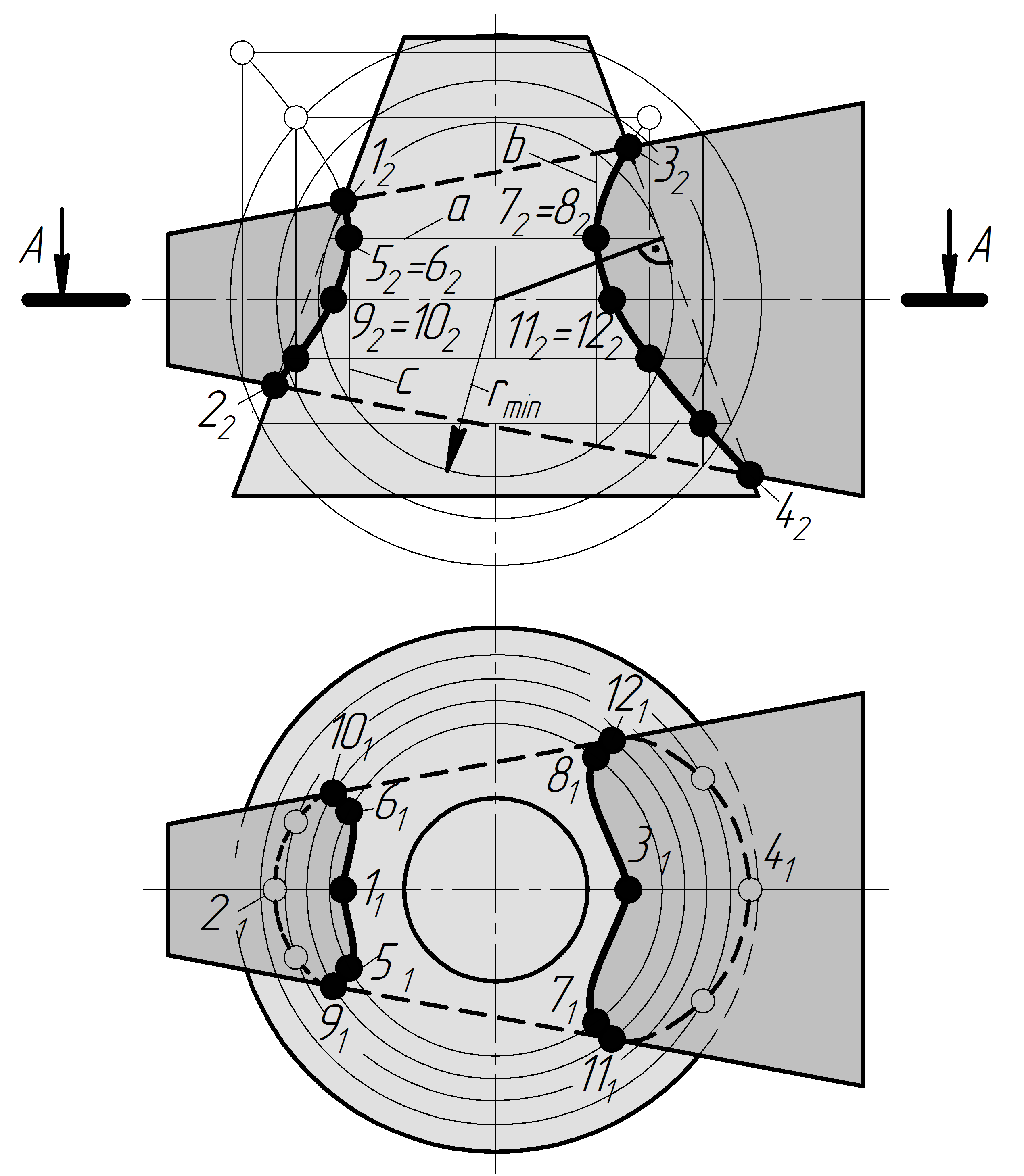
Рисунок 3.28

Подвійний дотик. У таблиці 3.1 приведені окремі випадки прикладу поверхонь обертання другого порядку, де лінія перетину розпадається на дві плоскі криві, які перетинаються. У кожному з випадків дві поверхні другого порядку, що перетинаються, дотикаються до третьої поверхні кулі (також другого порядку).

При цій умові має силу теорема Монжа, згідно якої дві поверхні другого порядку перетинаються і результатом перетину є дві плоскі криві другого порядку, якщо вони описані навколо третьої поверхні другого порядку або вписані в неї.

Таблиця 3.1 – Лінія перетину поверхонь обертання другого порядку

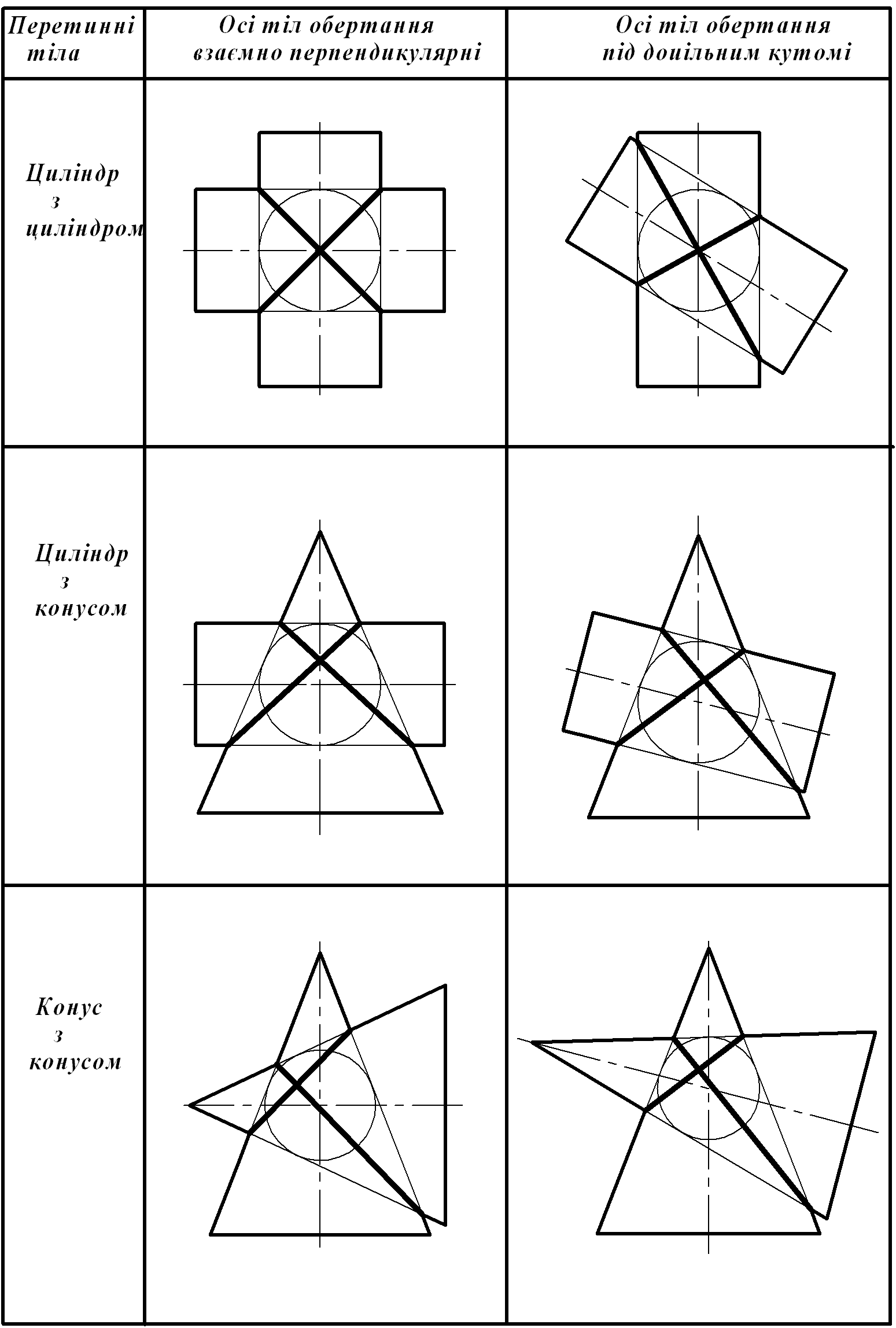
У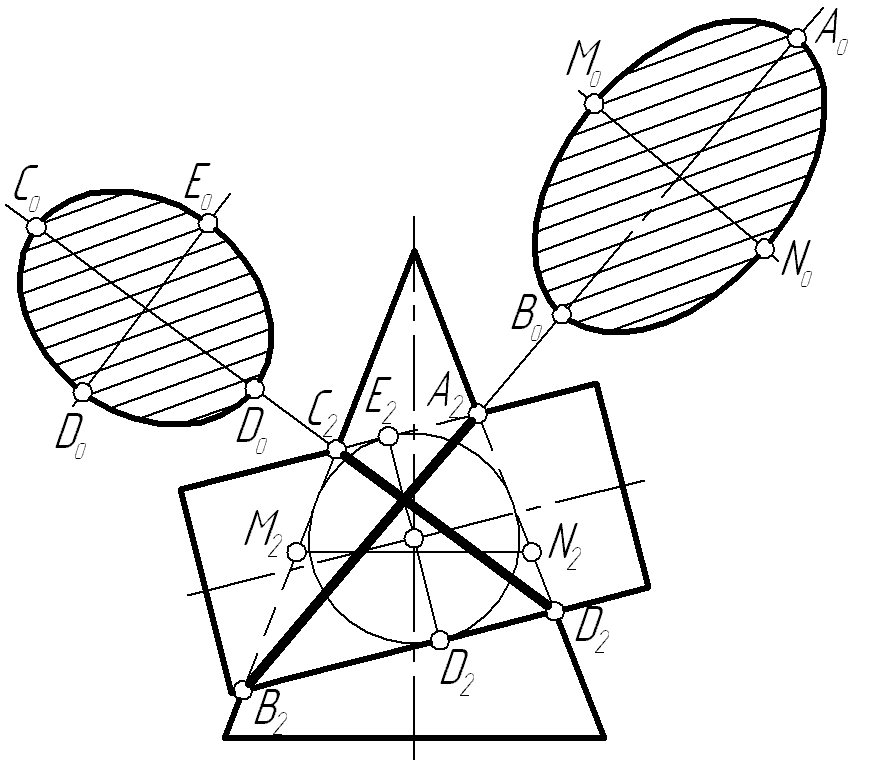 відповідності з цією теоремою лінії перетину двох циліндрів, двох конусів або циліндра з конусом, які описані навколо сфери, будуть плоскими кривими – еліпсами, фронтальні проекції яких є відрізками прямих (табл.3.1), на рисунку 3.29 винесеними перерізами є плоскі криві (еліпсів), які отримаємо при перетині циліндра з конусом, якщо останні описані навколо однієї і тієї ж кулі.

Рисунок 3.29