3.3 Взаємний перетин поверхонь

Перетин поверхонь між собою приводить до утворення ліній – кривих чи прямих, які є геометричним місцем точок, спільним для обох поверхонь. Ці лінії називаються лініями взаємного перетину або лініями переходу. Для побудови лінії перетину потрібно відшукати такі точки, які належали б одночасно двом заданим поверхням, що перетинаються. З’єднавши ці точки в певній послідовності, одержимо шукану лінію перетину. Лінії взаємного перетину можуть бути плоскими і просторовими.

Для визначення точок, які належать лінії перетину поверхонь тіл, застосовують метод посередників. Посередником може бути площина або сфера (спосіб площин і спосіб сфер). Спосіб допоміжних площин є універсальний і може успішно використовуватися в більшості випадків . Деколи при взаємному перетині поверхонь обертання більш простий розв’язок може дати спосіб сфер.

Рисунок 3.22

Алгоритм розв’язку задачі на визначення лінії перетину двох поверхонь наступний:

1. Вводимо допоміжну січну площину, яка перетинає кожну із заданих поверхонь за найбільш простими та вигідними для побудови лініями;

2. Визначаємо лінії перетину допоміжної площини із кожною із заданих поверхонь;

3. Знаходимо точки перетину побудованих ліній.

Принцип допоміжних сферичних перерізів грунтується на тому, що сфера з центром на осі будь-якої поверхні обертання перетинається з нею по колу, яке лежить в площині перпендикулярній до осі тіла (рис 3.23).

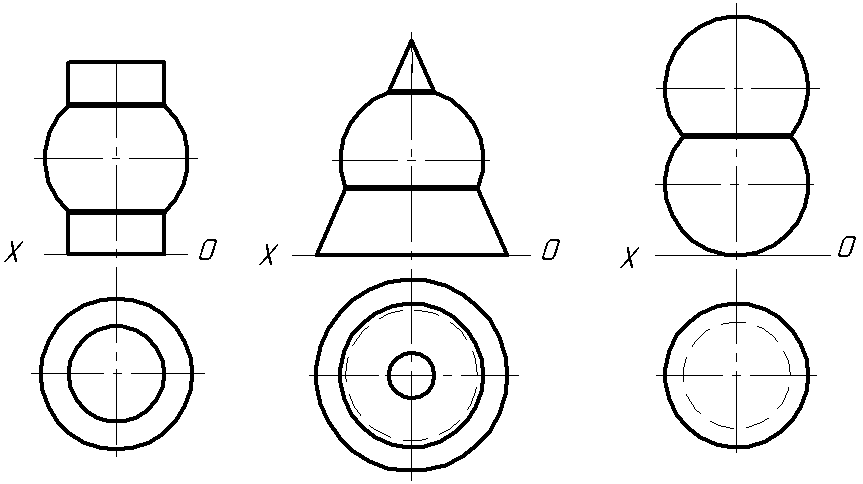Я кщо вісь тіла обертання паралельна одній із площин проекцій, тоді коло спроектується на дану площину проекцій у вигляді відрізка прямої, яка перпендикулярна до однойменної проекції осі тіла обертання.

а) б) в)

Рисунок 3.23 — Перетин: а) кулі з циліндром, б) кулі з конусом, в) взаємний перетин двох сфер

Задача 9 Побудувати проекції лінії перетину призми та прямого кругового конуса (рис. 8.3).

Розв’язок задачі подано на рис. 3.24,а,б,в,г у поетапному розв’язку, починаючи з умови задачі (рис. 3.24,а). У даному випадку лінія перетину буде складною. Вона складатиметься з кола, яке одержимо від перетину верхньої грані призми і конуса (рис.13.24,б) і двох парабол, що будуть мати спільні точки 9 і 10 (рис. 3.24,г). Вершини параболи будуть точками 3 і 4, пошук яких показано на рис. 3.24,в.

Для розв’язування цієї задачі і знаходження точок лінії перетину застосуємо допоміжну горизонтальну січну площину . Така площина перетинає призму прямокутником, а конус ─ колом (рис. 3.24). Це добре видно з наочного зображення для побудови точок 5, 6, 7, 8 за допомогою площини . За аналогією введемо ще одну січну площину  і знайдемо точки, які будуть належати лінії перетину. З’єднуємо у певній послідовності побудовані точки і дістаємо лінію перетину цих двох поверхонь – дві параболи, по яких бічні грані призми перетинають поверхню конуса.

а)

б)

Рисунок 3.24

в)