1. Проводять ряд допоміжних площин, які перетинають задану поверхню і площину;

2. Будують лінії перетину допоміжних площин з заданою поверхнею і площиною;

3. В перетині знайдених ліній відмічають точки шуканої лінії перетину.

При перетині лінійчастих поверхонь з площиною вигідно знаходити точки перетину твірних поверхні (прямих) із заданою площиною.

Задача 5 Задано прямий, коловий, горизонтально-проектуючий циліндр, який стоїть своєю основою на p₁ і перетинається січною площиною Σ. Знайти три проекції та дійсну величину перерізу (рис.3.16).

Для побудови проекцій перерізу, поверхню циліндра ділимо на однакову кількість рівних частин – на рис. 3.16 поділ зроблено на 8 частин. На горизонтальній проекції показано точки 1₁,2₁…,8₁. На фронтальній проекції проведено твірні, які перетинаються із січною площиною Σ в точках 1₂, 2₂….,8₂. Фронтальна проекція перерізу виродиться у відрізок 1₂7₂, який збігається з фронтальним слідом Σ₂ січної площини, а горизонтальна проекція перерізу збігається з горизонтальною проекцією циліндра. Профільна проекція в перерізі буде плавною кривою – еліпсом, велика вісь якого дорівнює відрізку 1₃5₃, а мала вісь – відрізку 3₃7₃. Проміжними точками еліпса є точки, отримані перетином відповідних твірних циліндра (2,4,6,8) з площиною . При побудові, коли січна площина проходить під кутом 45˚ до площини проекцій p₁, профільна проекція виродиться в коло, діаметр якого дорівнює діаметру основи циліндра. Дійсна величина еліпса може бути побудована, наприклад, одним із способів перетворення епюра (розділ 2). У даному випадку використаємо спосіб суміщення, що є найраціональніший для даної задачі.

Рисунок 3.16

Задача 6 Побудувати проекції та дійсну величину перерізу прямого кругового конуса фронтально-проекційною площиною  (рис.3.17, 3.18, 3.19).

Р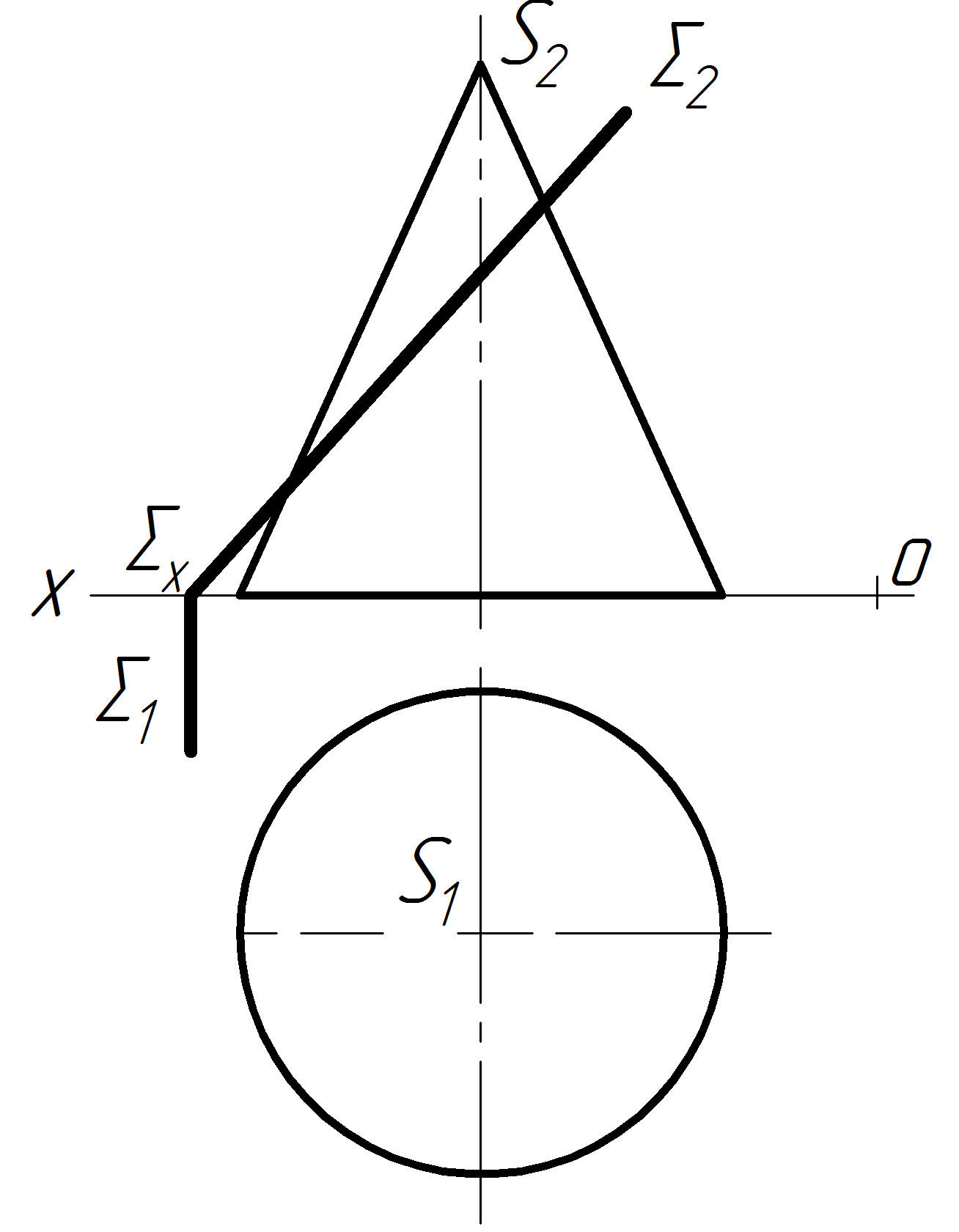 озв’язок показано поетапно на рисунках 3.17, 3.18, 3.19. У даному випадку січна площина перерізає конус по еліпсу, який співпадає із фронтальним слідом ₂ січної площини у пряму 1₂2₂, що буде великою віссю еліпса. Горизонтальна проекція осі визначається за точками 1₁2₁ (рис.3.18,а).

Д

Рисунок 3.17

ля знаходження малої осі еліпса ділимо фронтальну проекцію осі навпіл і через середину її проводимо горизонтальну площину . Фронтальна проекція малої осі вироджується в точку 3₂=4₂, а горизонтальна проекція буде відрізком 3₁4₁ (рис.3.18,б)_. Величина цього відрізка визначається у точках перетину кола, побудованого радіусом О₂К₂, з центру S₁, від перерізу конуса допоміжною площиною , з напрямком малої осі. Проміжними точками еліпса є точки, отримані перетином відповідних твірних конуса (SC, SD, SA, SB) із площиною  (рис.3.18,в та 3.18,г).

Дійсну величину фігури перерізу визначаємо способом суміщення площини ₃ з горизонтальною площиною ₁, або ж заміною площин проекцій, які описані у розділі 2.

а)

б)

г)

в)

Рисунок 3.18

Рисунок 3.19

З адача 7 Побудувати проекції та дійсну величину перерізу прямого кругового конуса фронтально-проекційною площиною  (рис.3.20).

На рис.3.20 конус перетинається фронтально-проекційною площиною, яка паралельна твірній конуса. Лінією перетину буде парабола, для побудови якої проводимо допоміжні горизонтальні площини (, , ), які перетинають конус по колах, а площину  — по її горизонталях. На перетині цих ліній лежать шукані точки параболи.

Фронтальна проекція перерізу співпадає з фронтальним слідом площини , а на горизонтальній площині p₁ проектується у вигляді параболи. Дійсна величина параболи знайдена шляхом суміщення площини  з площиною проекцій p₁ (розділ 2).

Рисунок 3.20

Задача 8 Побудувати переріз конуса фронтальною площиною  (рис.3.21).

П ерерізом конуса буде гіпербола, оскільки січна площина паралельна p₂, але не проходить через вісь конуса, тому гіпербола спроектується на площину p₁ у вигляді прямої, яка збігатиметься із слідом ₁, а на площину p₂ — у дійсну величину. Характерні точки гіперболи 6 і 7, в яких вона перетинає площину p₁ і коло основи конуса зі слідом _1.

Щ

Рисунок 3.21

е одна характерна точка гіперболи — вершина 1. Горизонтальна проекція 1₁ знаходиться на середині відрізка 6₁7₁. Для побудови фронтальної проекції 1₂ проводимо з точки S₁ коло радіусом R=S₁1₁. Щоб знайти фронтальну проекцію цього кола, проводимо лінію зв’язку до перетину з крайньою твірною конуса. Знаходимо місце знаходження цього кола на фронтальній площині і точки 1₂ на ньому. Допоміжні точки гіперболи 2, 3, 4, 5 можна знайти за допомогою допоміжних січних площин  і , яка аналогічна побудові точки 1.