1 Суть методу проекцій. Види проекцій

В основі побудови довільного зображення лежить метод проекцій, який полягає в тому, що в просторі вибираємо довільну точку за центр проеціювання і площину, яка називається площиною проекцій. Для того, щоб спроеціювати на площину проекцій будь-яку точку, достатньо через центр проекцій і цю точку провести пряму, яка називається проекційним променем, до перетину її з площиною проекцій. Точка перетину променя з площиною є проекцією вибраної нами точки.

Залежно від вибраного центру проекцій розрізняють центральне і паралельне проеціювання, і відповідно, центральні і паралельні проекції.

1.1 Центральні та паралельні проекції

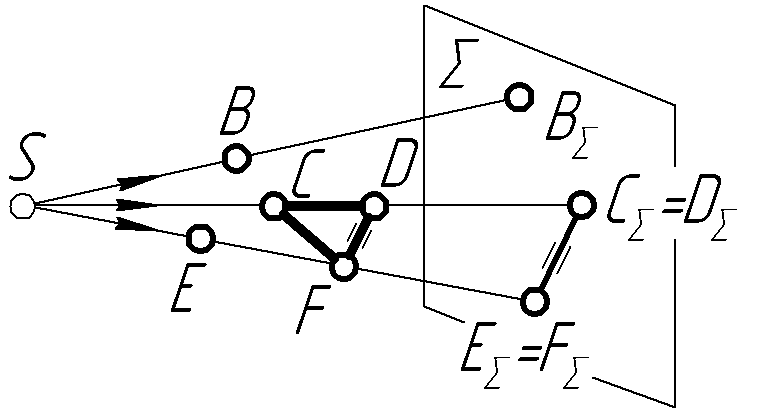
При центральному проеціюванні (рис.1.1) проеціюючі промені приймаються за такі, що виходять з однієї точки S, яка знаходиться на кінцевій віддалі від площини проекцій Σ. Ця точка називається центром проекцій або полюсом.

П ри проеціюванні кривої лінії множина променів, які проведені через точки кривої, утворюють конічну поверхню (рис.1.1), тому центральні проекції називають також конічними або полярними.

Ц

Рисунок 1.1 – Центральні проекції

ентральну проекцію будь-якого предмета називають також ще перспективою. В цьому випадку центром проекцій є точка зору спостерігача. Центральні проекції використовують в інженерно-будівельних кресленнях, а також у малярському мистецтві, оскільки вони є найбільш

наочними, але будуються порівняно складно, невигідні для вимірювання, а тому в машинобудівних кресленнях мають обмежене застосування.

При паралельному проеціюванні центр проекцій передбачається віддаленим у безкінечність, тому проекційні промені паралельні між собою (рис. 1.2).

Таким чином, замість центру проекцій, тут задається напрямок проеціювання. Множина проекційних променів, які проведені через точки заданої кривої лінії, утворюють циліндричну поверхню (рис.1.2), тому паралельні проекції називають також циліндричними.

Перевагою паралельних проекцій є простота побудови креслень, а також легкість вимірювання потрібних величин. Недоліком є менша наочність у порівнянні з центральними проекціями.

Рисунок 1.2 – Паралельні проекції

П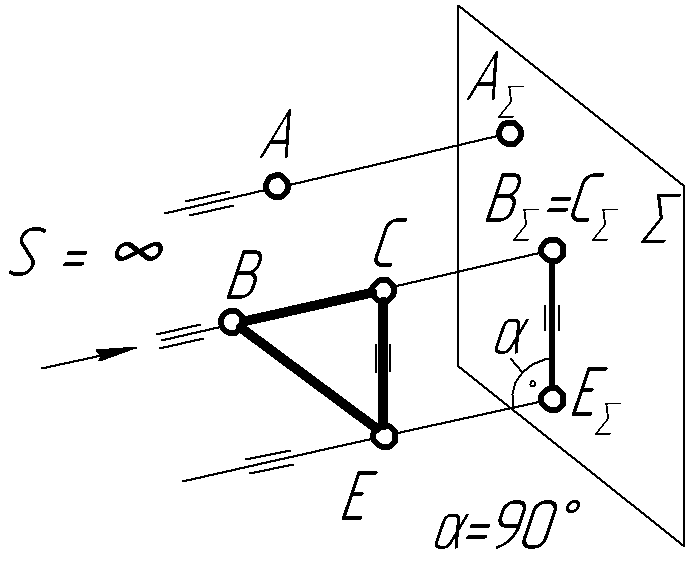 аралельні проекції широко використовуються в машинобудівних кресленнях.

Залежно від направлення проеціюючого променя відносно площини проекцій є два види паралельних проекцій: прямокутні і косокутні.

П

Рисунок 1.3 – Прямокутні проекції

рямокутними називаються такі паралельні проекції, в яких напрямок проеціювання перпендикулярний до площини проекцій (рис.1.3); косокутними – такі, в яких напрямок проеціювання складає з площиною проекцій кут, відмінний від прямого.

Прямокутні проекції часто називають ортогональними проекціями, слово “ортогональні” в буквальному перекладі означає “прямокутні” (від грецьких слів “ортос” – прямий і “гонос” – кут).

Загальні властивості паралельних проекцій.

• Проекцією точки є точка.

• Проекцією прямої лінії є пряма.

• Якщо точка лежить на прямій, то проекція цієї точки належить проекції прямої; те саме можна сказати про проекцію точки, яка лежить на кривій лінії.

• Якщо відрізок паралельний до площини проекцій, то він спроеціюється на площину проекцій без спотворень (в дійсну величину).

• Якщо пряма розміщена паралельно до напрямку проеціювання, то проекції всіх точок цієї прямої збігаються з проекцією прямої, яка є точкою на площині проекцій.

• Якщо прямі або криві лінії перетинаються в просторі, то проекції цих ліній також перетинаються.

• Проекції відрізків однієї і тієї ж прямої лінії пропорційні самому відрізку.

• Проекції двох паралельних прямих паралельні між собою.

• Відношення проекцій відрізків двох паралельних прямих дорівнює відношенню цих відрізків.