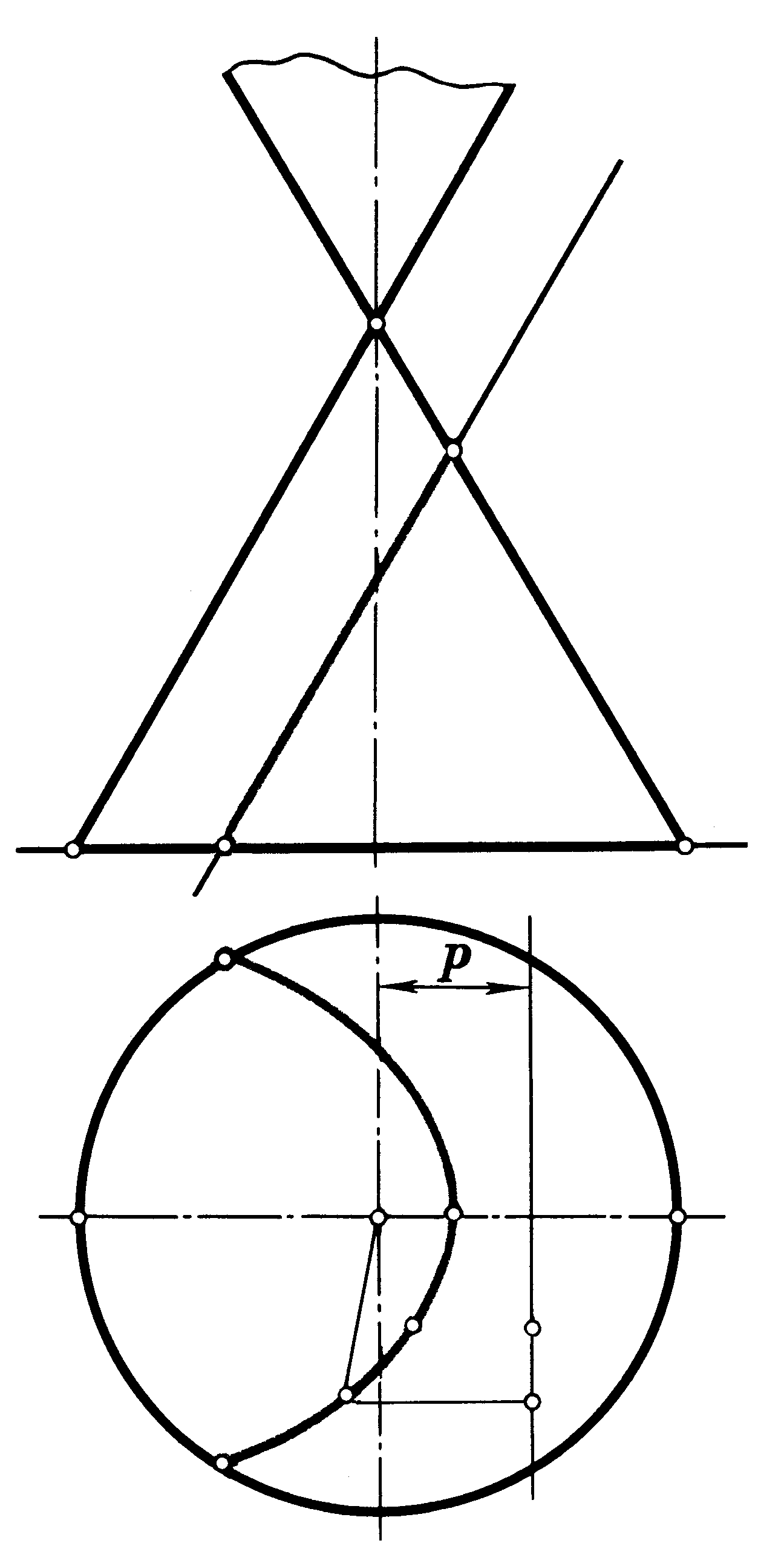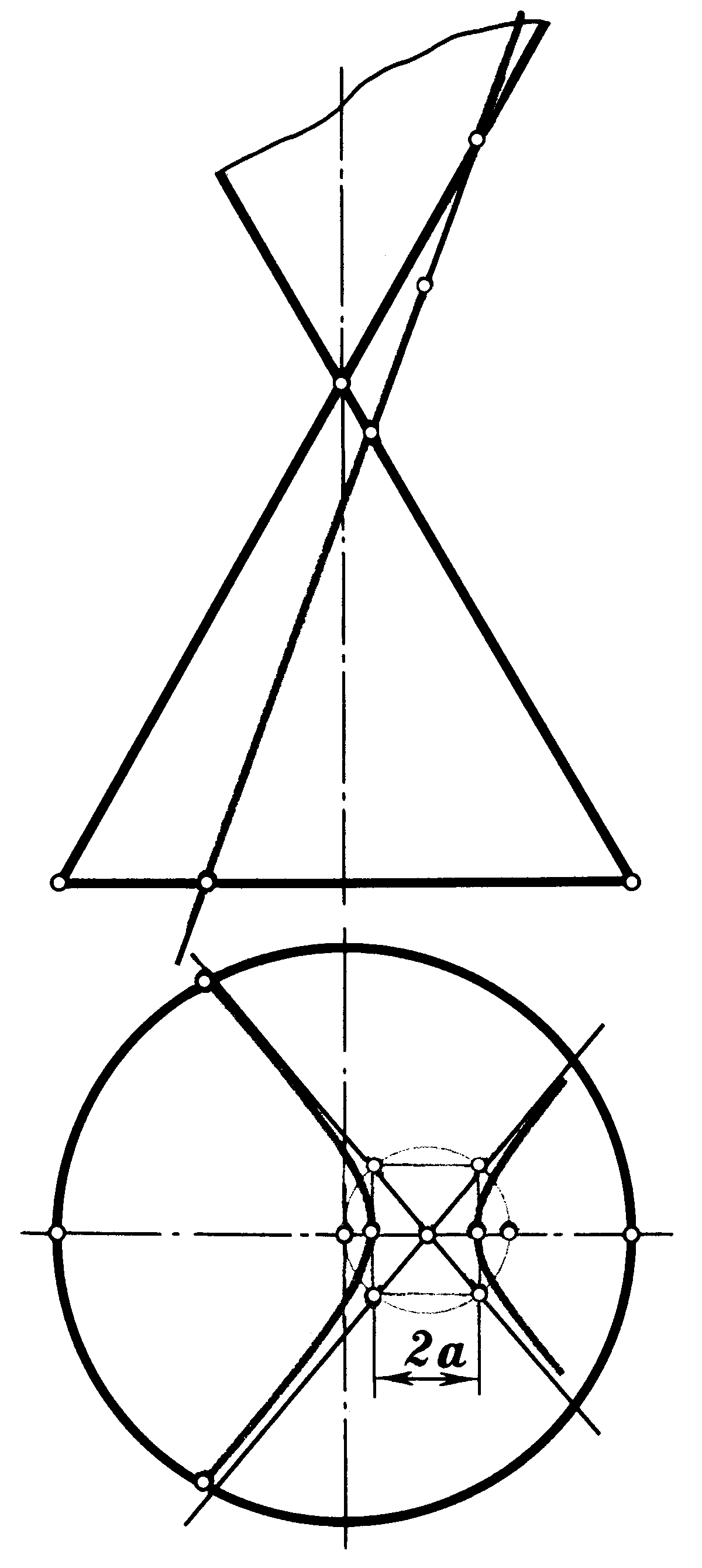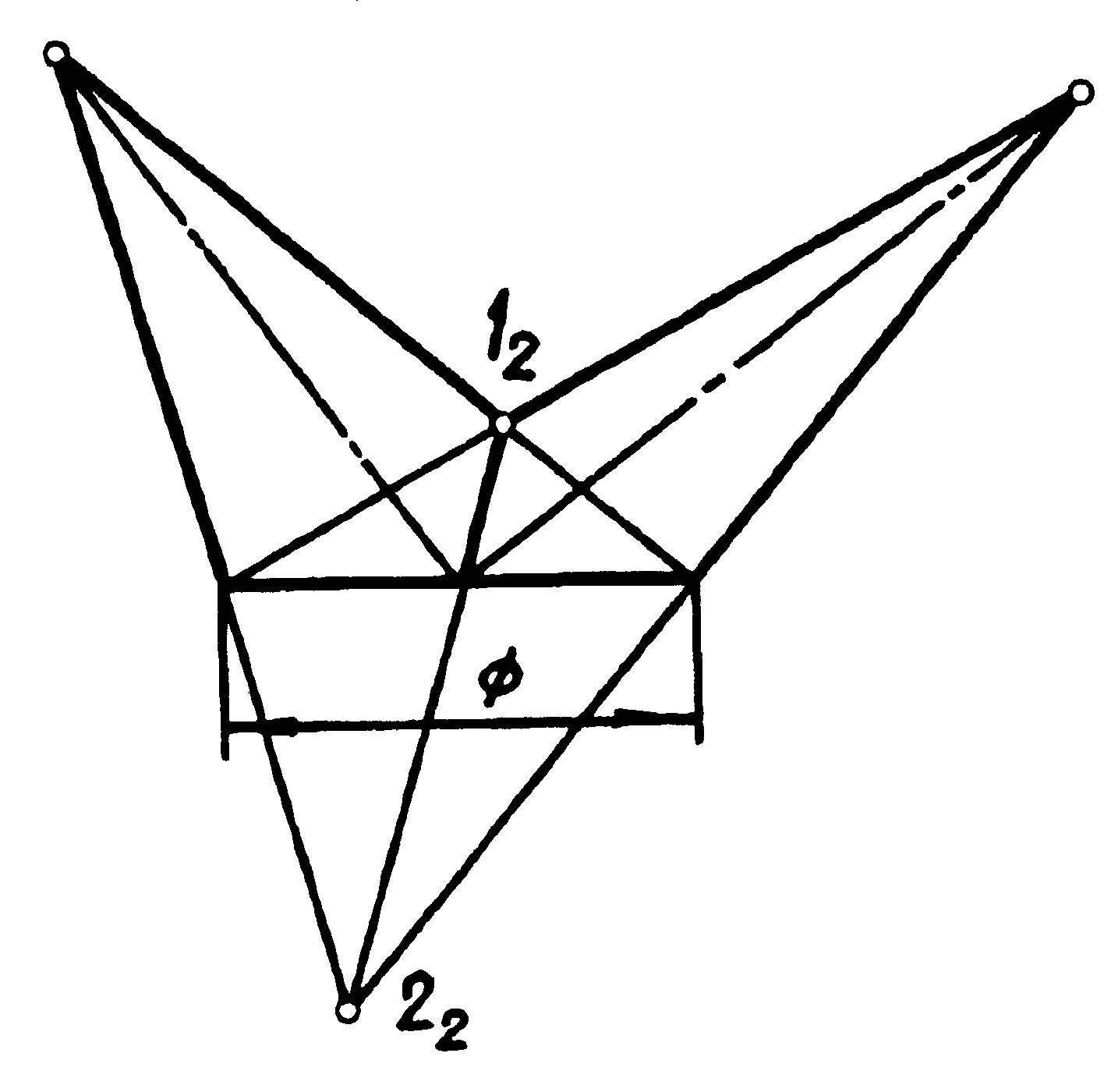6 Поверхні обертання.

ВЗАЄМНИЙ ПЕРЕТИН ПОВЕРХОНЬ ОБЕРТАННЯ

(6год, П10, П11, П12)

Навести відповіді та виконати графічні побудови в робочому зошиті на поставлені запитання

6.1 Яким чином утворюються поверхні обертання і який вигляд має їх визначник?

Поверхні обертання утворюються обертанням плоскої або просторової лінії l (твірної) навколо осі і . Визначник такої поверхні має вигляд Ф(l, і )[A].

6.2 Які лінії утворюють ортогональну сітку поверхонь обертання? Наведіть їх назви і як вони утворюються?

Поверхня обертання вміщує в собі два каркаси ліній – паралелі і меридіани, які утворюють ортогональну сітку її.

6.3 Які лінії на поверхні обертання називають екватором, а які шийкою?

Найбільшу з паралелей називають екватором, а найменшу – шийкою.

6.4 Яким чином на кресленні задають поверхню обертання?

Креслення поверхні обертання, яке складається із проекцій осі і твірної, важке для уявлення. Тому на кресленні поверхню обертання задають проекціями осі, головного меридіана і екватора, які утворюють обрис поверхні на відповідних площинах проекцій.

6.5 Яким чином на кресленні за заданими віссю обертання і твірною будують головний меридіан поверхні?

1) через точки твірної проводять паралелі поверхні;

2) будують точки головного меридіана як результат перетину паралелей з головною меридіанною площиною (тобто з площиною рівня, яка проходе через вісь поверхні обертання).

6.6 Які поверхні обертання називають поверхнями другого порядку?

Поверхні обертання описуються алгебраїчним рівнянням. Степінь рівняння алгебраїчної поверхні визначає її порядок. Тому поверхні обертання другого порядку описуються алгебраїчним рівнянням другого степеня. Графічно порядок поверхні можна визначити за числом точок перетину її з прямою лінією (ураховуються точки як дійсні, так і уявні).

6.7 Запишіть теорему про перетин двох алгебраїчних поверхонь.

Теорема. Дві алгебраїчні поверхні перетинаються між собою по алгебраїчній кривій, порядок якої дорівнює добутку порядків поверхонь: N = n₁ × n₂ .

6.8 По яким лініям поверхня обертання другого порядку може пересікатися із січною площиною, назвіть їх.

 Поверхня обертання 2-го порядку із січною площиною може пересікатися по кривим другого порядку:

 по колу, еліпсу

 по параболі,

 по гіперболі ,

або по двом прямим:

6.9 Сфера із січною площиною перетинається по колу .

6.10 Поверхня циліндру обертання в залежності від розташування січної площини відносно неї може бути перерізаною по:

 колу ,

 еліпсу , або

 по двом прямим .

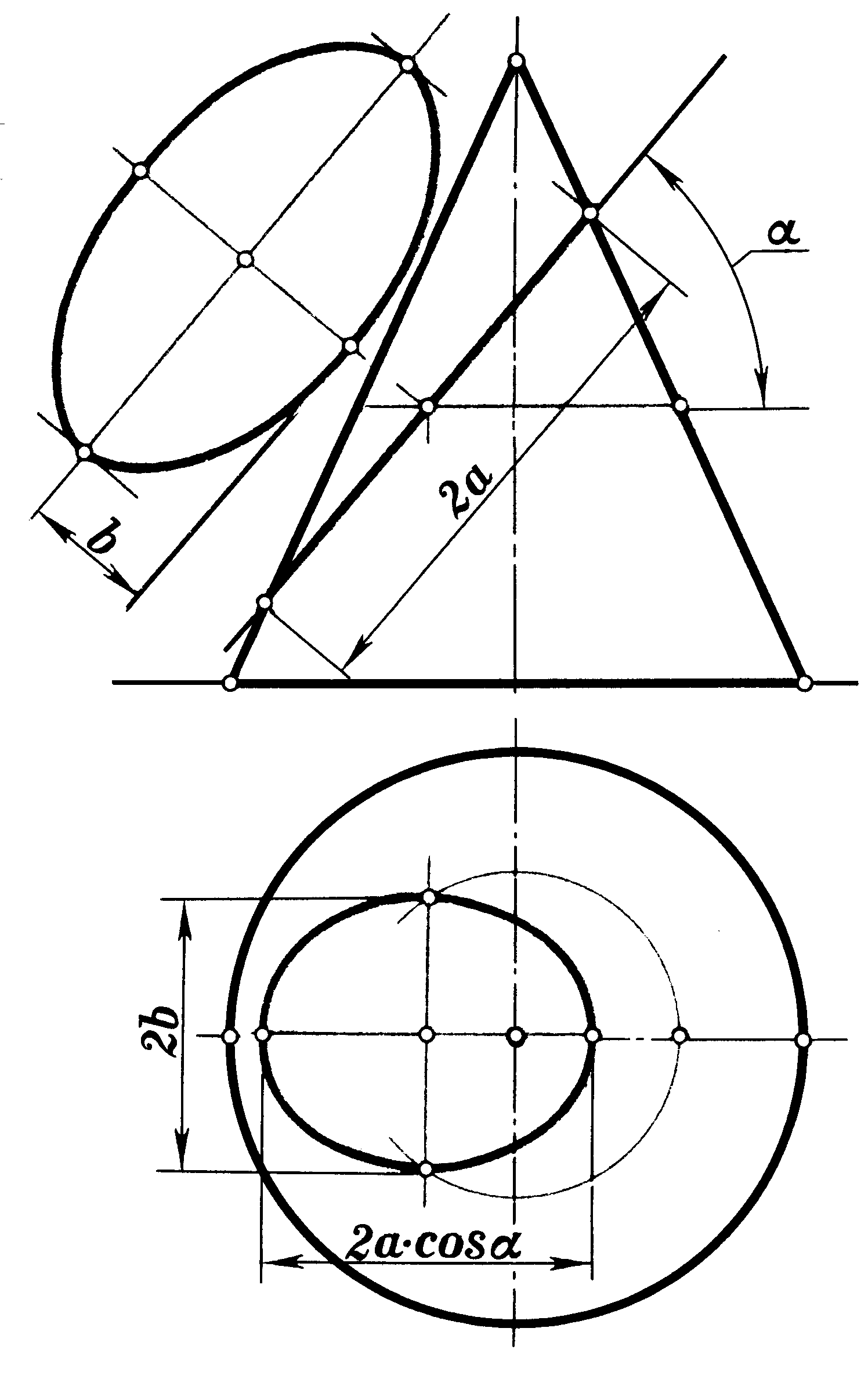
6.11 Назвіть назву лінії перерізу конічної поверхні січною площиною (рисунки 6.1; 6.2; 6.3). Відповіді наведіть у таблиці 6.1.

Таблиця 6.1 – Відповіді на запитання 6.11

Рисунок	Назва лінії перерізу конічної поверхні січною площиною і як вона розташована відносно конічної поверхні
6.1	еліпс
6.2	парабола
6.3	гіпербола

Рисунок 6.1	Рисунок 6.2	Рисунок 6.3

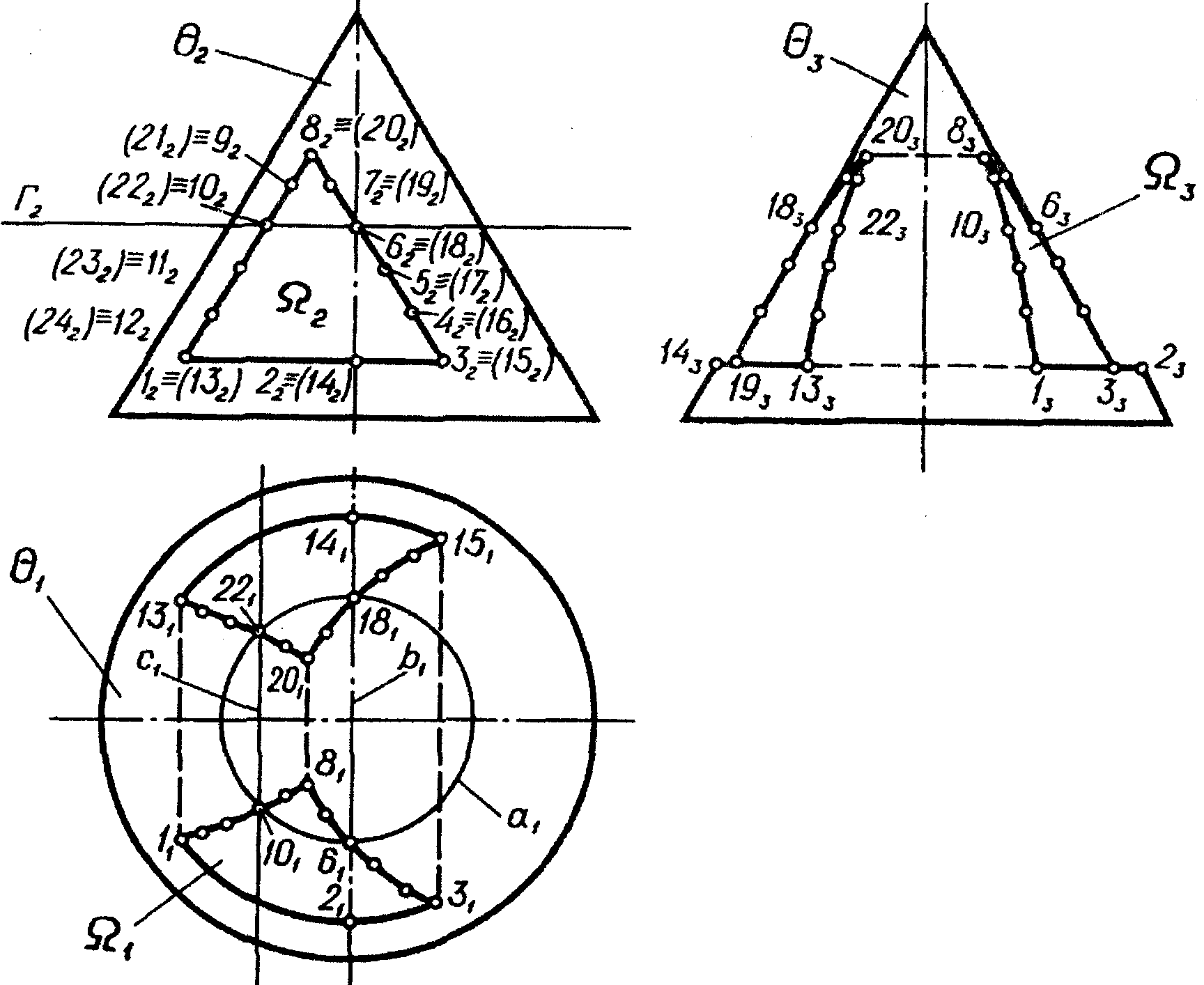
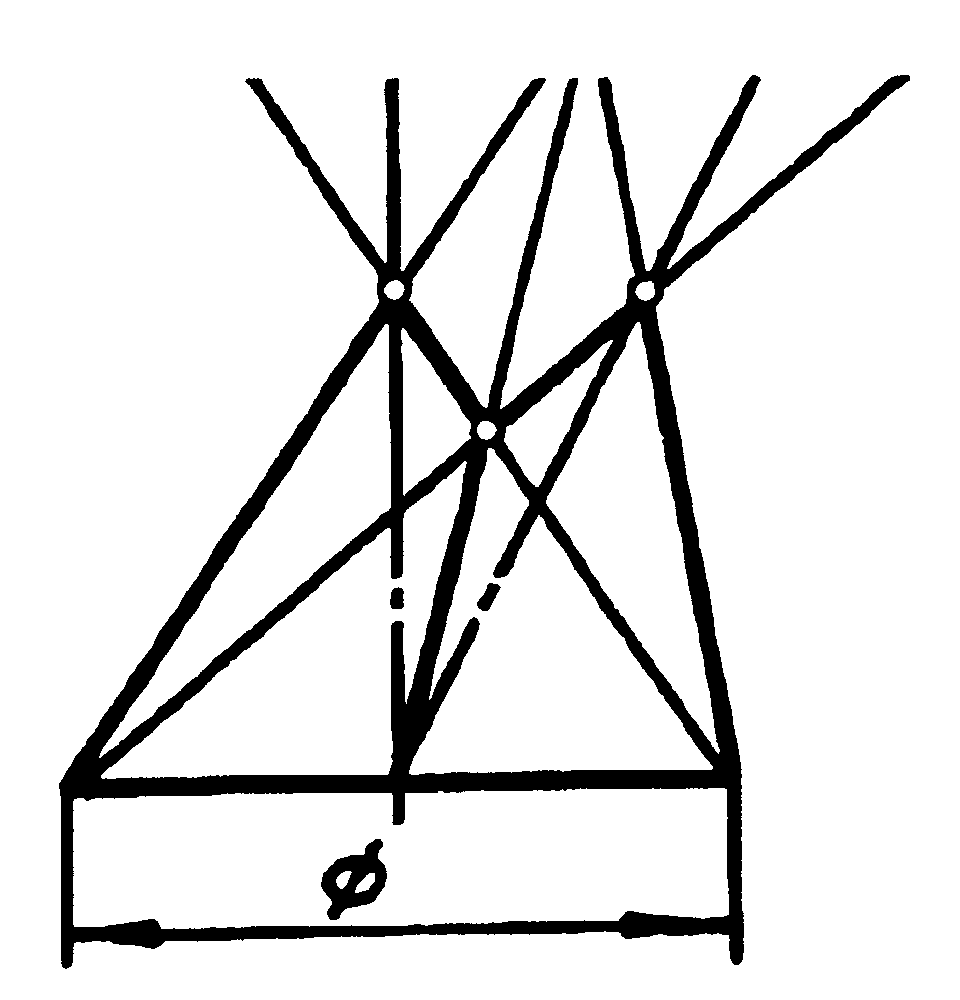
6.12 На рисунку 6.4 наведене креслення конусу, поверхня якого перерізана призматичним вікном. Грані вікна перерізали конічну поверхню по відповідним лініям. Назвати ці лінії, відповіді записати у таблицю 6.2. Визначити, яким способом побудовані проекції ліній перетину конічної поверхні з гранями призматичного вікна.

Рисунок 6.4

Таблиця 6.2 – Відповіді на запитання 6.12

Назва грані призми	Назва лінії перерізу конічної поверхні гранями призматичного вікна і обґрунтуйте цей тип лінії
1 8	парабола, січна площина паралельна до одної твірної конуса
3 8	парабола, січна площина паралельна до одної твірної конуса
1 3	частина кола, січна площина перпендикулярна до осі конуса

 Проекції ліній перетину поверхні конусу гранями призматичного вирізу побудовані за допомогою способу допоміжних січних горизонтальних площин.

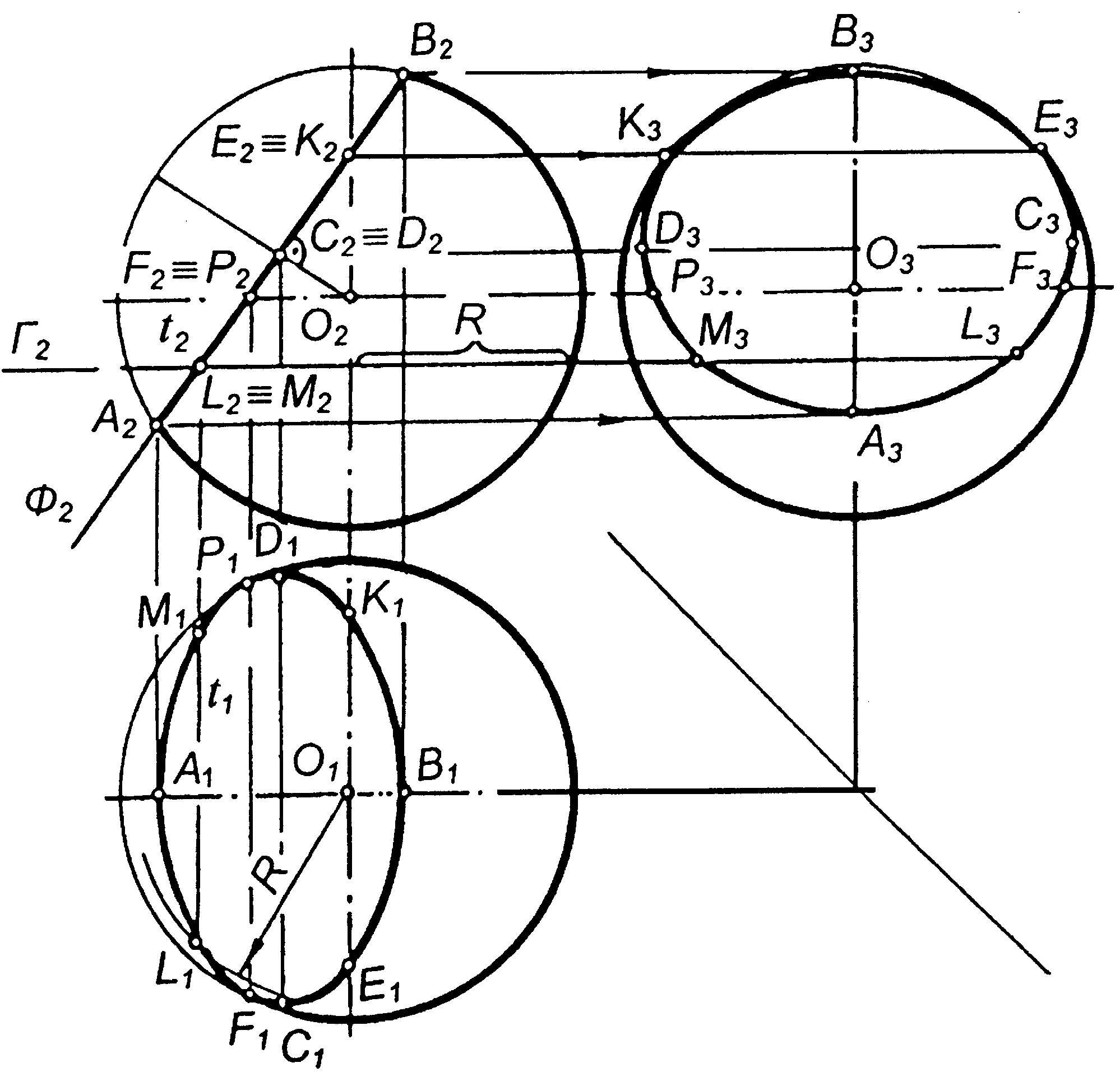
6.13 По якій лінії перерізана куля фронтально-проекційною площиною Ф (рисунок 6.5) і яким чином вона спроекціювалась на площини проекцій П₁, П₂, П₃ ? Яким способом побудовані проекції точок перерізу кулі фронтально-проекційною площиною Ф ?

Рисунок 6.5

Відповідь: куля перерізана фронтально-проекційною площиною Ф по колу, проекціями якого на площини проекцій П₁ і П₃ є еліпс, а на П₂  пряма .

Для побудови проекцій точок лінії перерізу кулі площиною застосований спосіб допоміжних січних горизонтальних площин .

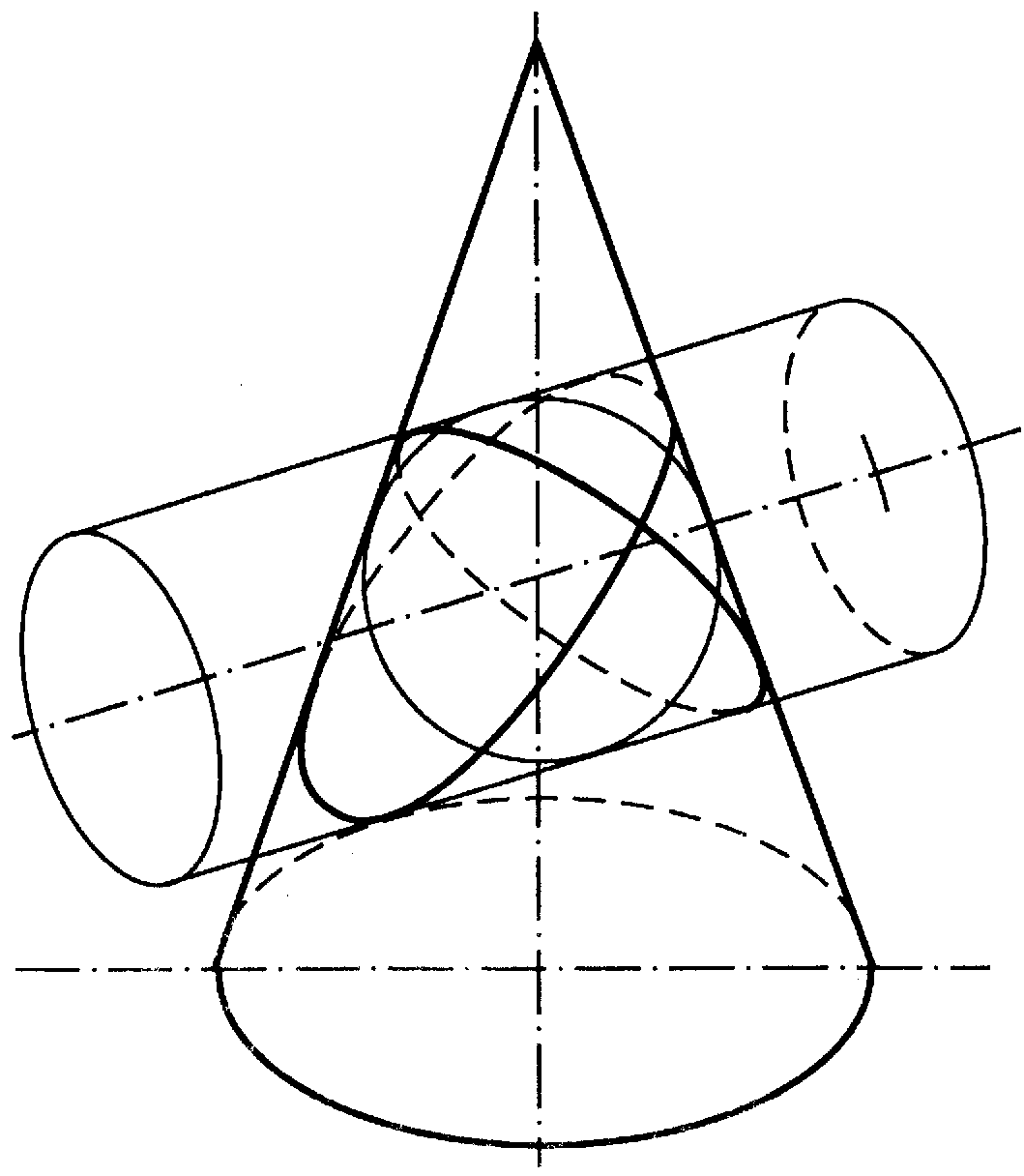
6.14 Запишіть теорему Монжа про розпадання кривої 4-го порядку при взаємному перетинанні двох поверхонь 2-го порядку на дві плоскі криві другого порядку (рисунок 6.6).

Рисунок 6.6

Теорема Монжа. Якщо дві поверхні другого порядку описані навколо третьої, то вони перетинаються по двом плоским кривим, площини яких проходять через точки перетину ліній дотику

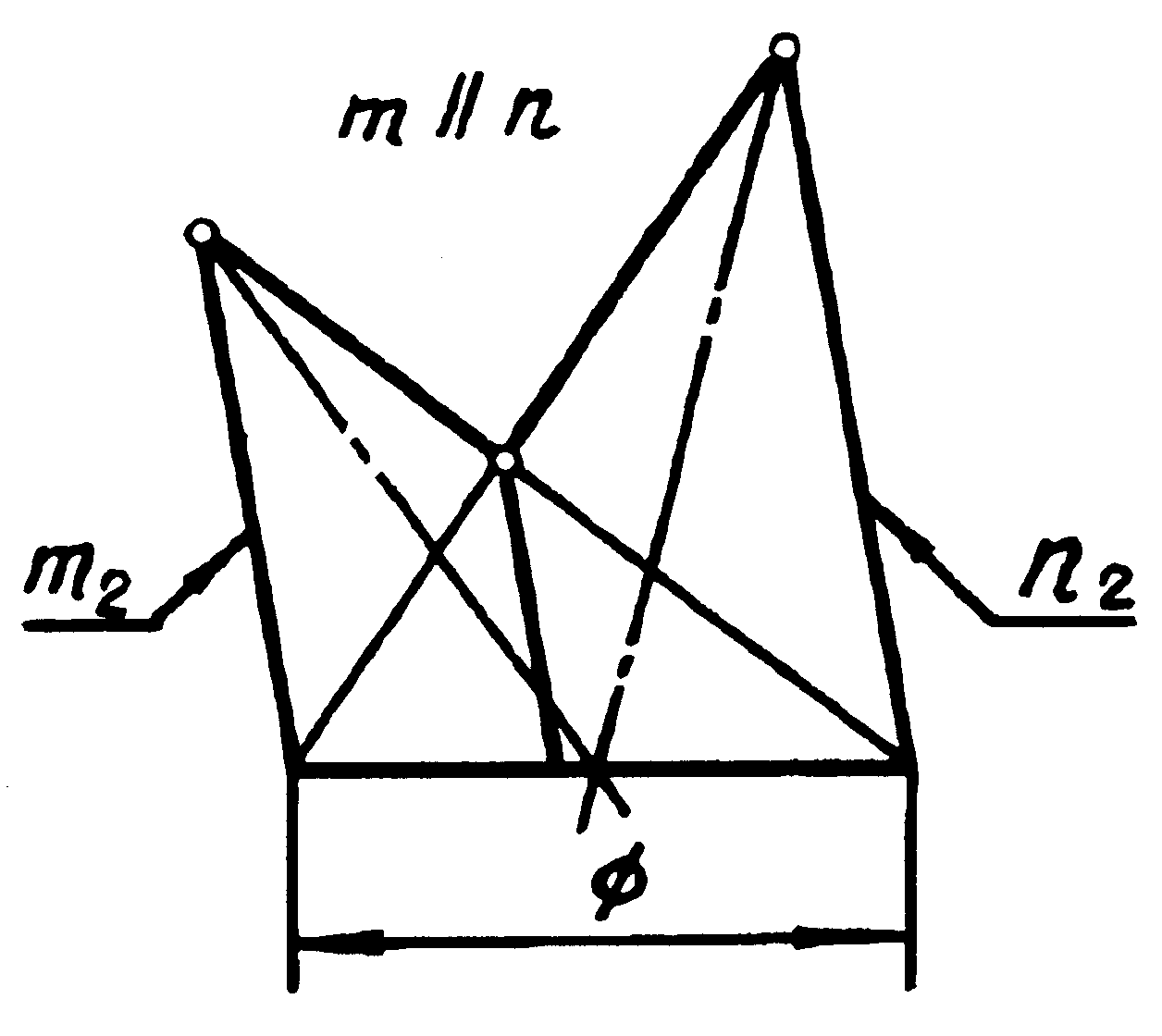
6.15 Визначити, за якими лініями перетинаються дві поверхні, що задані на рисунках 6.7; 6.8; 6.9. Відповідь наведіть у таблиці 6.3.

Рисунок 6.7	Рисунок 6.8	Рисунок 6.9

Таблиця 6.3 – Відповіді на запитання 6.15

Рисунок	Назва ліній перетину заданих поверхонь і чому саме такі лінії
6.7	Коло і частина еліпсу (всі твірні обох конусів перетинаються між собою)
6.8	Коло і парабола (очеркові твірні двох конусів паралельні)
6.9	Коло і гіпербола (перетинаються дві половини обох конусів)

6.16 Який спосіб застосований для побудови проекцій лінії перетину двох поверхонь, що наведені на рисунках 6.10 і 6.11? У чому він полягає?

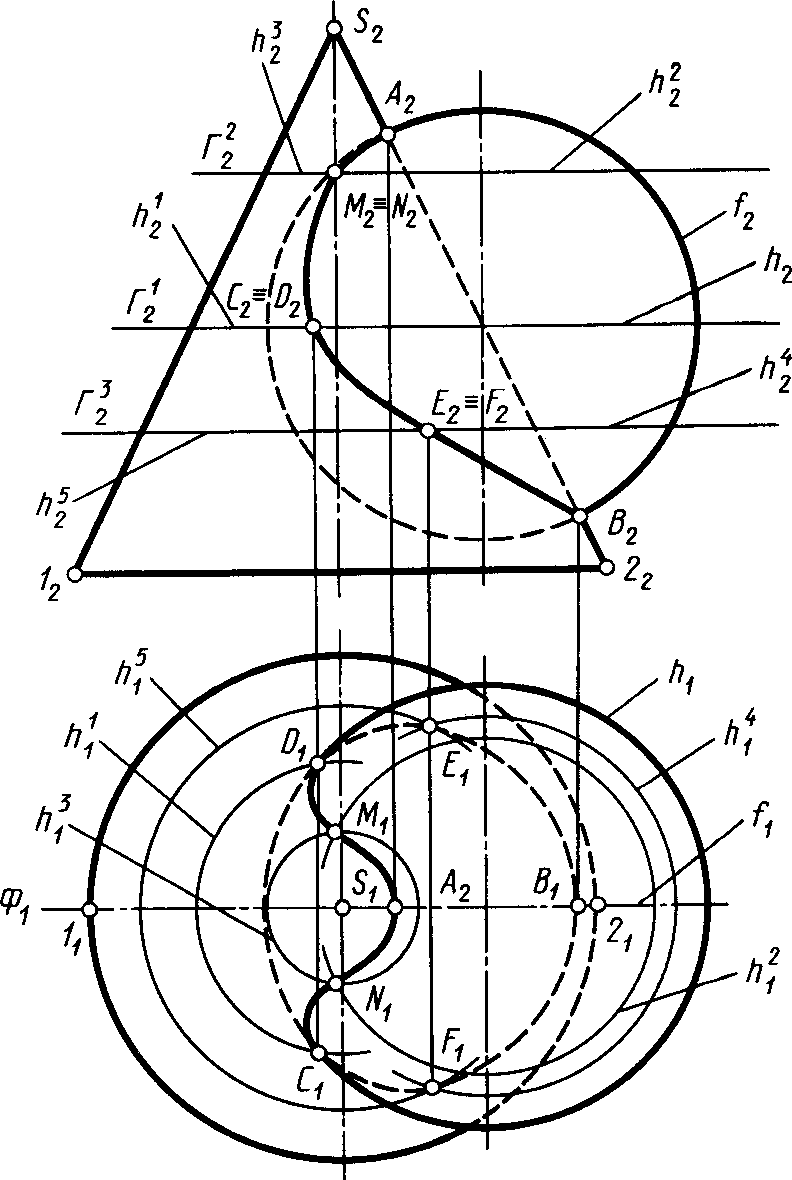
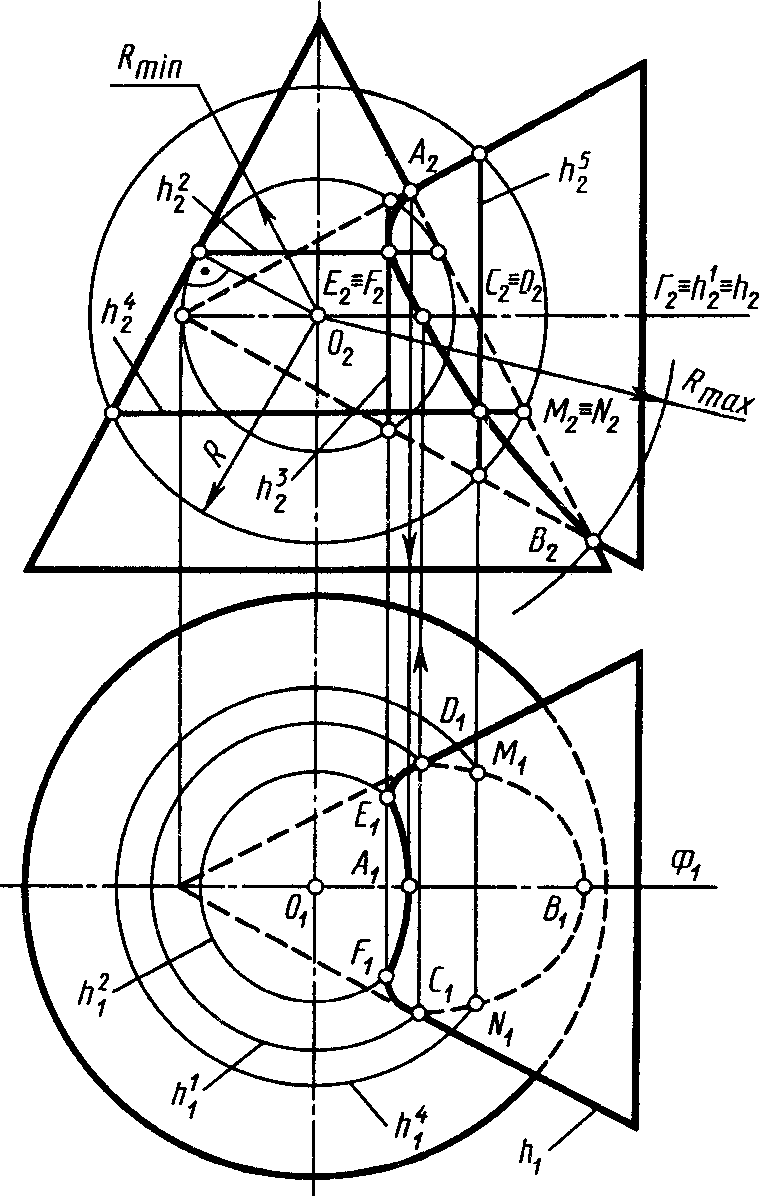
Відповідь. Для побудови проекцій ліній перетину двох поверхонь застосований спосіб додаткових січних поверхонь: на рисунку 6.10 – горизонтальних січних площин, а на рисунку 6.11 – концентричних сфер.

Вибрані додаткові січні поверхні перетинають обидві поверхні по графічно простим лініям – по колам, які перетинаючись між собою утворюють точки ліній перетину цих поверхонь.

6.17 Назвіть вид проекцій на П₁ і П₂ просторової лінії 4-го порядку як перетину двох заданих поверхонь обертання другого порядку (рисунки 6.10; 6.11).

До рисунку 6.10

Просторова крива 4-го порядку як результат перетину поверхонь прямого кругового конусу і сфери має проекцію:

на П₂ у вигляді параболи,

на П₁ у вигляді кривої 4-го порядку.

Рисунок 6.10	Рисунок 6.11

До рисунку 6.11

Просторова крива 4-го порядку як результат перетину двох поверхонь прямого кругового конусу має проекцію:

на П₂ у вигляді гіперболи,

на П₁ у вигляді кривої 4-го порядку.

6.18 Наведіть алгоритм розв’язування задач на побудову лінії перетину двох поверхонь

1) Аналізують умову задачі. З’ясовують вигляд заданих поверхонь, їх порядки і положення у просторі та відносно одна до одної. Визначають порядок лінії перетину та порядок її проекцій.

Якщо дві поверхні, що перетинаються, мають спільну площину симетрії і вона паралельна до будь-якої площини проекцій, то проекція просторової кривої на площину симетрії зменшує свій порядок у два рази. Вид проекції лінії перетину двох поверхонь обертання 2-го порядку на площину симетрії такий:

 при перетині сфери з іншими поверхнями обертання 2-го порядку  парабола;

 при перетині конусів і циліндрів між собою у будь-яких комбінаціях  гіпербола.

2) Будують усі головні точки лінії перетину.

3) Будують декілька проміжних точок.

4) Будують плавний обвід проекцій точок і визначають видимість проекцій.

5) Перевіряють правильність розв’язування задачі (чи отриманий результат, якого чекали?).