5 Багатогранники.

ВЗАЄМНИЙ ПЕРЕТИН БАГАТОГРАННИКІВ (4 год, П8, П9)

Навести відповіді та виконати графічні побудови в робочому зошиті на поставлені запитання

5.1 Дати відповіді на запитання стосовно креслення, що наведене на рисунку 5.1.

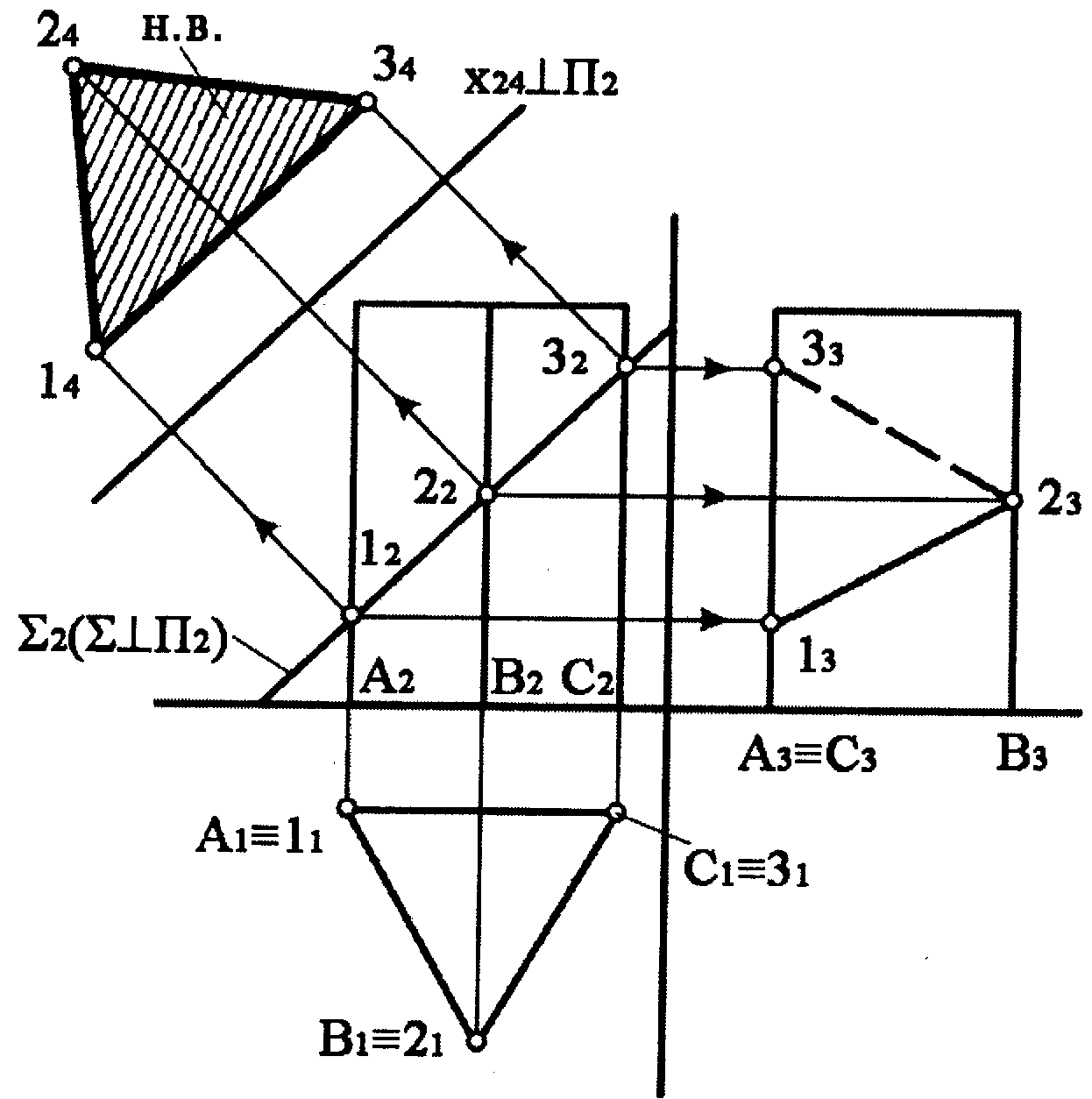
Рисунок 5.1

1) Який багатогранник заданий на рисунку?

 На рисунку 5.1 заданий багатогранник, що називається тригранна пряма призма.

2) З яких багатокутників складаються грані багатогранника?

 Грані багатогранника складаються з прямокутників .

3) Які положення у просторі займають ребра і грані багатогранника?

 Ребра багатогранника займають горизонтально-проекційне положення. Дві грані займають горизонтально-проекційне положення, а одна грань фронтальне положення.

4) Яке положення у просторі займає січна площина  ?

 Січна площина  займає фронтально-проекційне положення.

5) По якій фігурі січна площина  перетинає багатогранник і чому?

 Січна площина  перетинає багатогранник по трикутнику тому що вона перетинає три грані багатогранника.

6) По якому найбільшому багатокутнику може перетинати січна площина заданий багатогранник і яким чином вона повинна бути розташовано відносно заданого багатогранника?

 Січна площина може перетинати заданий багатогранник по

п’ятикутнику, якщо вона буде розташовано відносно багатогранника таким чином, що перетинатиме всі п’ять граней багатогранника .

7) Яким способом на рисунку 5.1 визначена фігура перерізу багатогранника січною площиною?

 Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ребер багатогранника з фронтальним слідом-проекцією січної площини.

8) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?

 Натуральна величина фігури перерізу багатогранника січною площиною визначена способом заміни площин проекцій.

5.2 Дати відповіді на запитання стосовно креслення, що наведене на рисунку 5.2.

1) Який багатогранник заданий на рисунку?

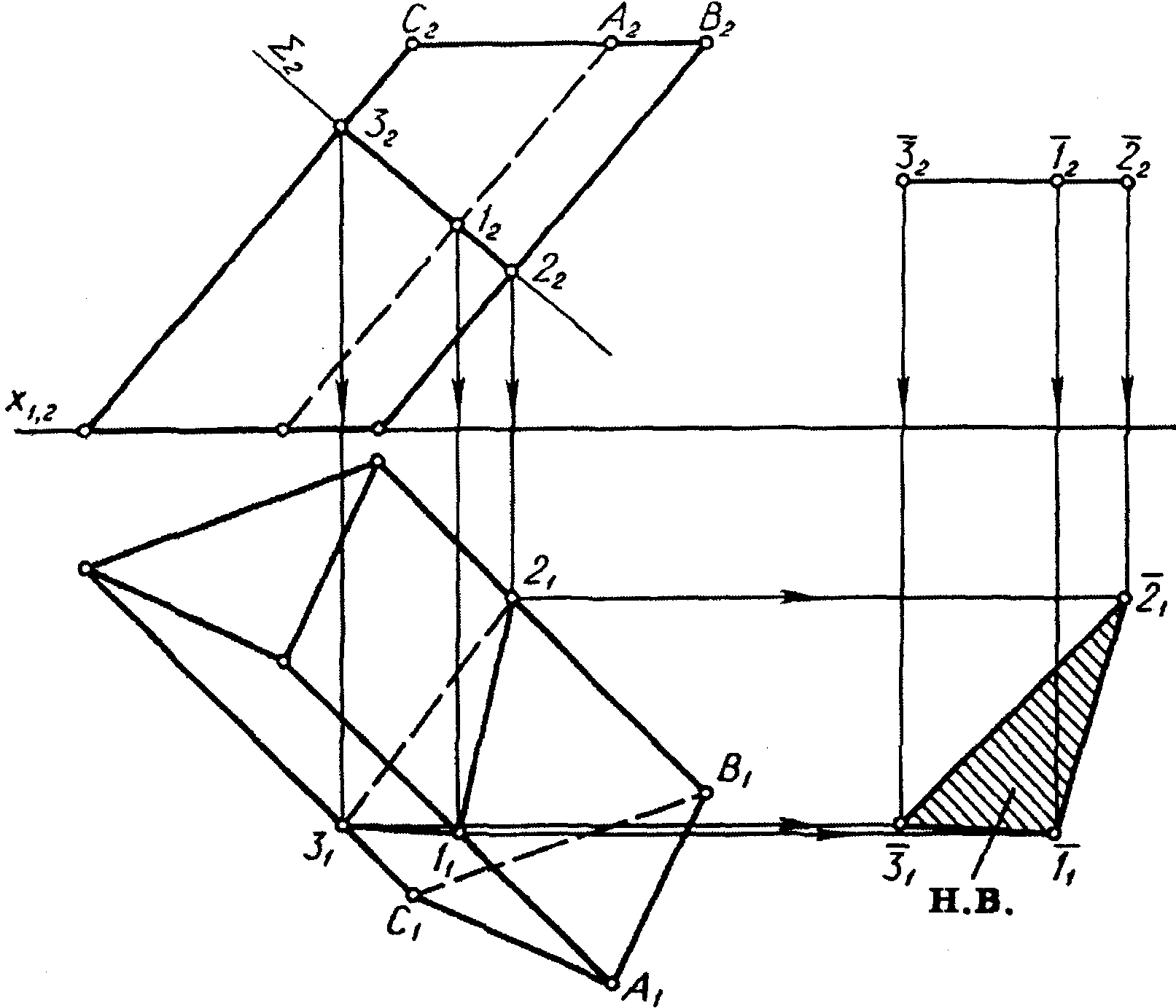
 На рисунку 5.2 заданий багатогранник, що називається тригранна похила призма.

2) З яких багатокутників складаються грані багатогранника?

 Грані багатогранника складаються з паралелограмів .

3) Які положення у просторі займають ребра і грані багатогранника?

 Ребра і грані багатогранника займають загальне положення.

4) Яке положення у просторі займає січна площина  ?

 Січна площина  займає фронтально-проекційне положення.

5) По якій фігурі січна площина  перетинає багатогранник і чому?

 Січна площина  перетинає багатогранник по трикутнику, тому що вона перетинає три грані багатогранника.

6) Яким способом на рисунку 5.2 визначена фігура перерізу багатогранника січною площиною?

 Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ребер багатогранника з фронтальним слідом-проекцією січної площини.

7) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?

 Натуральна величина фігури перерізу багатогранника січною площиною визначена способом плоско паралельного переміщення .

Рисунок 5.2

5.3 Дати відповіді на запитання стосовно креслення, що наведене на рисунку 5.3.

1) Який багатогранник заданий на рисунку?

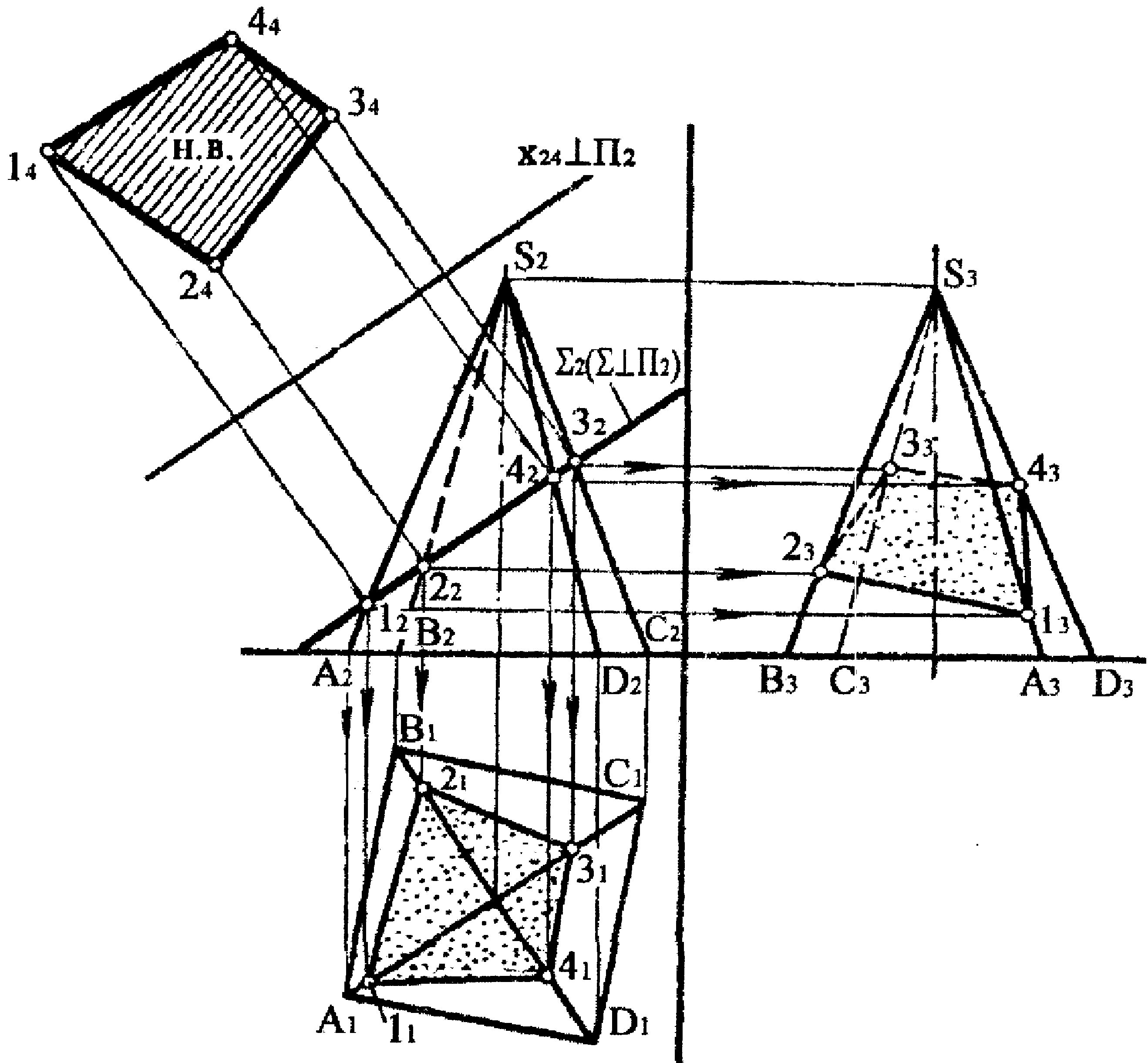
 На рисунку 5.3 заданий багатогранник, що називається чотиригранна піраміда.

2) З яких багатокутників складаються грані багатогранника?

 Грані багатогранника складаються з трикутників .

3) Які багатогранники називають тетраедрами?

 Тетраедром називають тригранну піраміду, у якій бокові грані і основа є правильні трикутники.

Рисунок 5.3

4) Які положення у просторі займають ребра і грані багатогранника, що наведений на рисунку 5.3?

 Ребра і грані багатогранника займають загальне положення.

5) Яке положення у просторі займає січна площина  ?

 Січна площина  займає фронтально-проекційне положення.

6) По якій фігурі січна площина  перетинає багатогранник і чому?

 Січна площина  перетинає багатогранник по чотирикутнику, тому що вона перетинає чотири грані багатогранника.

7) Яким способом на рисунку 5.3 визначена фігура перерізу багатогранника січною площиною?

 Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ребер багатогранника з фронтальним слідом-проекцією січної площини.

8) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?

 Натуральна величина фігури перерізу багатогранника січною площиною визначена способом заміни площин проекцій.

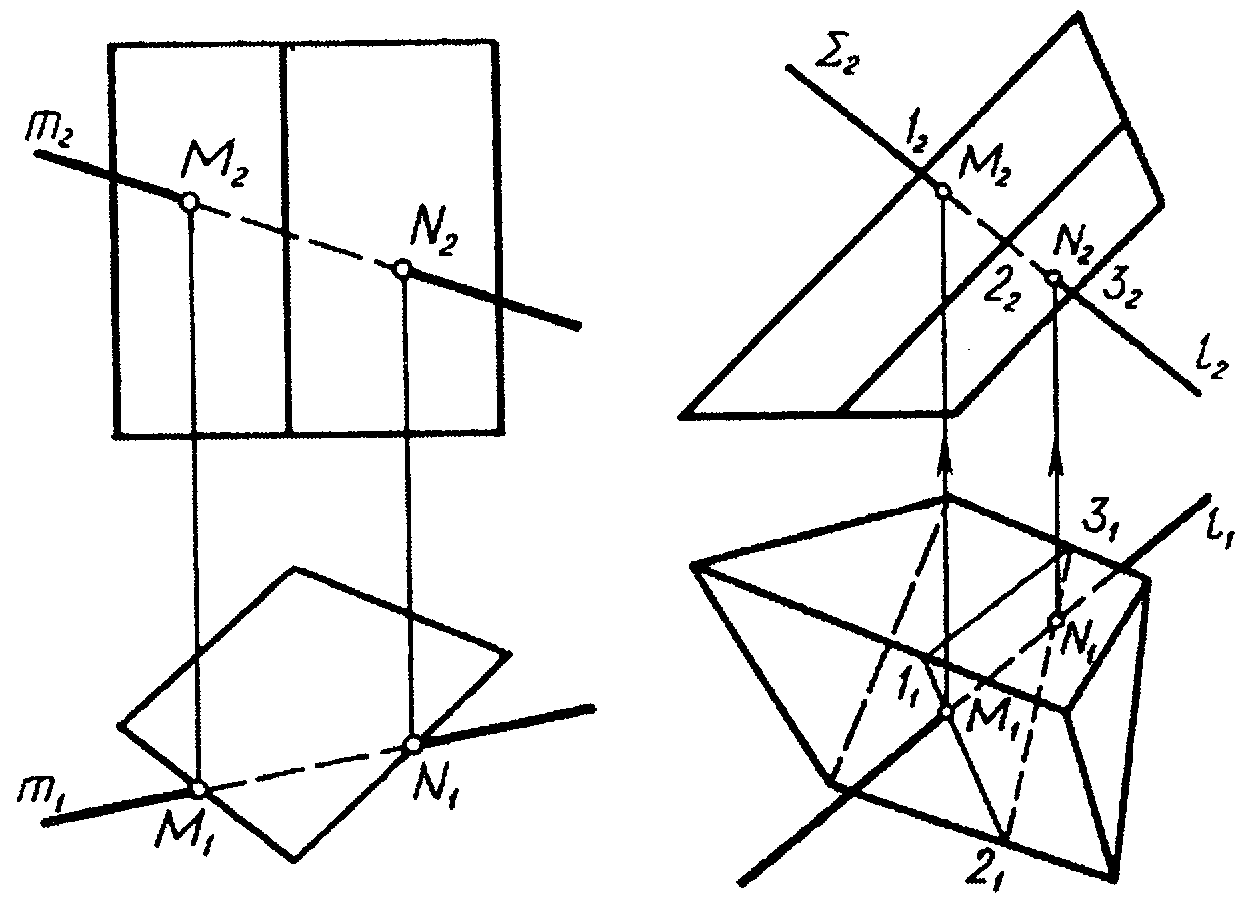
5.4 Наведіть алгоритм побудови точок перетину прямої з чотирьохгранної призмою (рисунок 5.4 а, б) одночасно для двох рисунків а) і б).

а) б) Рисунок 5.4

1) Через пряму проводимо допоміжну фронтально-проекційну площину, яка перетинатиме багатогранники на рис. а) по чотириграннику, а на рисунку б) – по трикутнику.

2) Перетин горизонтальних проекцій багатогранників перерізу призм січною площиною з горизонтальною проекцією прямої визначає точки входу та виходу прямої відносно багатогранника.

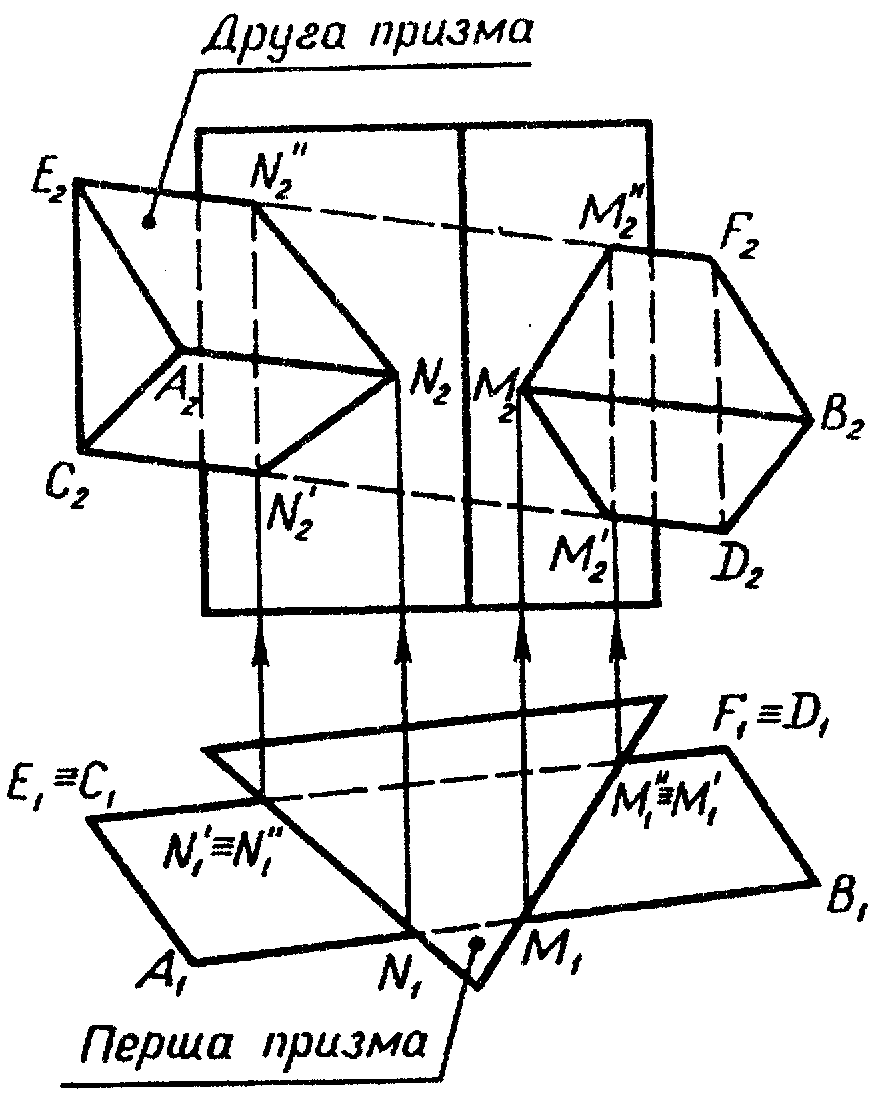
5.5 Навести алгоритм побудови проекцій лінії перетину двох призм, що наведені на рисунку 5.5.

1) Будуємо точки перетину ребер другої призми з двома гранями першої призми, що займають положення фронтально-проекційних площин.

2) З’єднуємо між собою отримані точки у кожній грані .

Рисунок 5.5