Алгоритм побудови лінії перетину двох площин

1) Дії для побудови першої спільної точки 3 заданих двох площин:

1.1Через пряму ОР проводимо допоміжну горизонтально-проекційну площину;

1.2 Будуємо лінію n перетину допоміжної горизонтально-проекційної площини з площиною трикутника ІКМ;

1.3 Визначаємо точку 3 як результат перетину прямих n і ОР.

2) Дії для побудови другої спільної точки 6 заданих двох площин:

2.1 Через пряму ОТ проводимо допоміжну фронтально-проекційну площину;

2.2 Будуємо лінію m перетину допоміжної фронтально-проекційної площини з площиною трикутника ІКМ;

2.3 Визначаємо точку 6 як результат перетину прямих m і ОT.

3) З’єднуємо точки 3 і 6 і отримаємо лінію перетину двох площин.

4) Встановлюємо видимість на епюрі (поясніть, яким чином) за до-помогою конкуруючих точок. Наприклад, на П₂ виділяємо точку перетину 5₂ фронтальних проекцій О₂Т₂ і К₂М₂. Це не є спільною точкою перетину двох трикутників. З точки 5₂ проводимо лінію вертикального проекційного зв’язку до горизонтальної проекції сторін трикутників до перетину із сторонами О₁Т₁ і М₁К₁. І ту точку, що найбільш віддалена від П₂, будемо бачити на П₂. Це точка, що розташована на прямій МК. Значить у точці 5₂ на П₂ будемо бачити фронтальну проекцію К₂М₂ сторони КМ.

Аналогічно визначаємо видимість проекцій сторон трикутників на П₁.

4 СПОСОБИ ПЕРЕТВОРЕННЯ ЕПЮРУ (4 год, П6, П7)

Навести відповіді та виконати графічні побудови в робочому зошиті на поставлені запитання

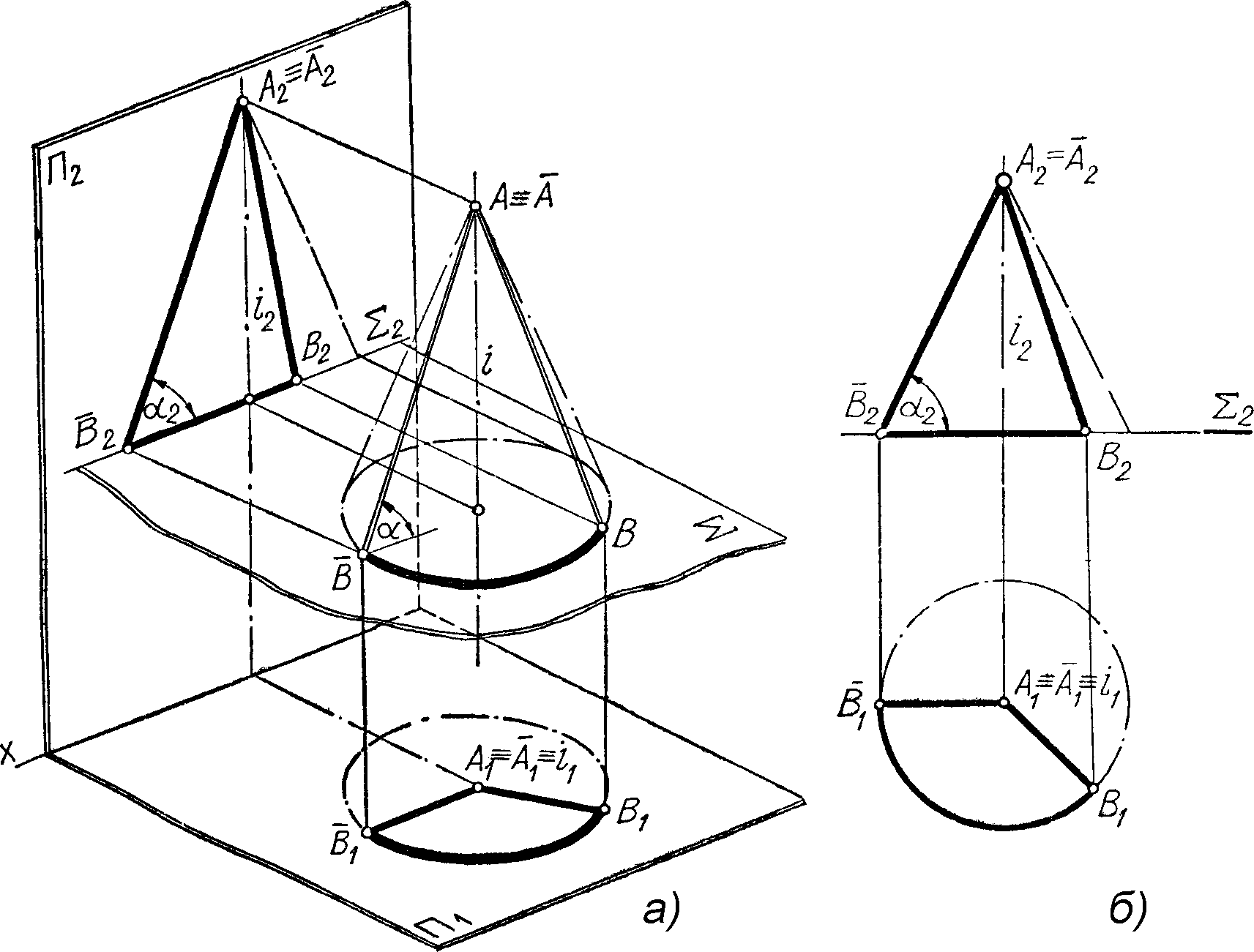
4.1 Навести алгоритм, який застосовують для розв’язання завдань способом обертання навколо осі стосовно прикладу, що наведений на рисунку 4.1:

Рисунок 4.1 – Визначення дійсної величини відрізка АВ і кута нахилу його до П1 способом обертанням навколо горизонтально-проекційної осі; а) наочне зображення, б) побудови на епюрі

1 Задають вісь обертання i, перпендикулярну до площини проекцій П₁. Якщо цю ось провести через будь-який кінець відрізку, наприклад, через точку А, то обертати необхідну тільки одну точку В, бо інша, точка А, як розташована на осі обертання буде нерухомою.

2 Визначають площину обертання S точки В навколо осі. Вона завжди перпендикулярна до осі обертання, а значить буде площиною рівня (горизонтальною). На епюрі вказують сліди-проекції цієї площини S₂ .

3 Визначають центр обертання (центри обертання всіх точок фігури розташовуються на осі обертання) як результат перетину осі обертання з площиною обертання.

4 Визначають радіус обертання та його величину (для цього сполучають центр обертання з точкою В).

5 Визначають нове положення фігури після процесу обертання. Для цього будують спочатку переміщену горизонтальну проекцію за траєкторією кола до положення, за яким нова горизонтальна проекція відрізку стане паралельною до осі x₁₂, а потім  на фронтальній площині проекцій по вертикальній лінії проекційного зв’язку на сліді-проекції площини обертання

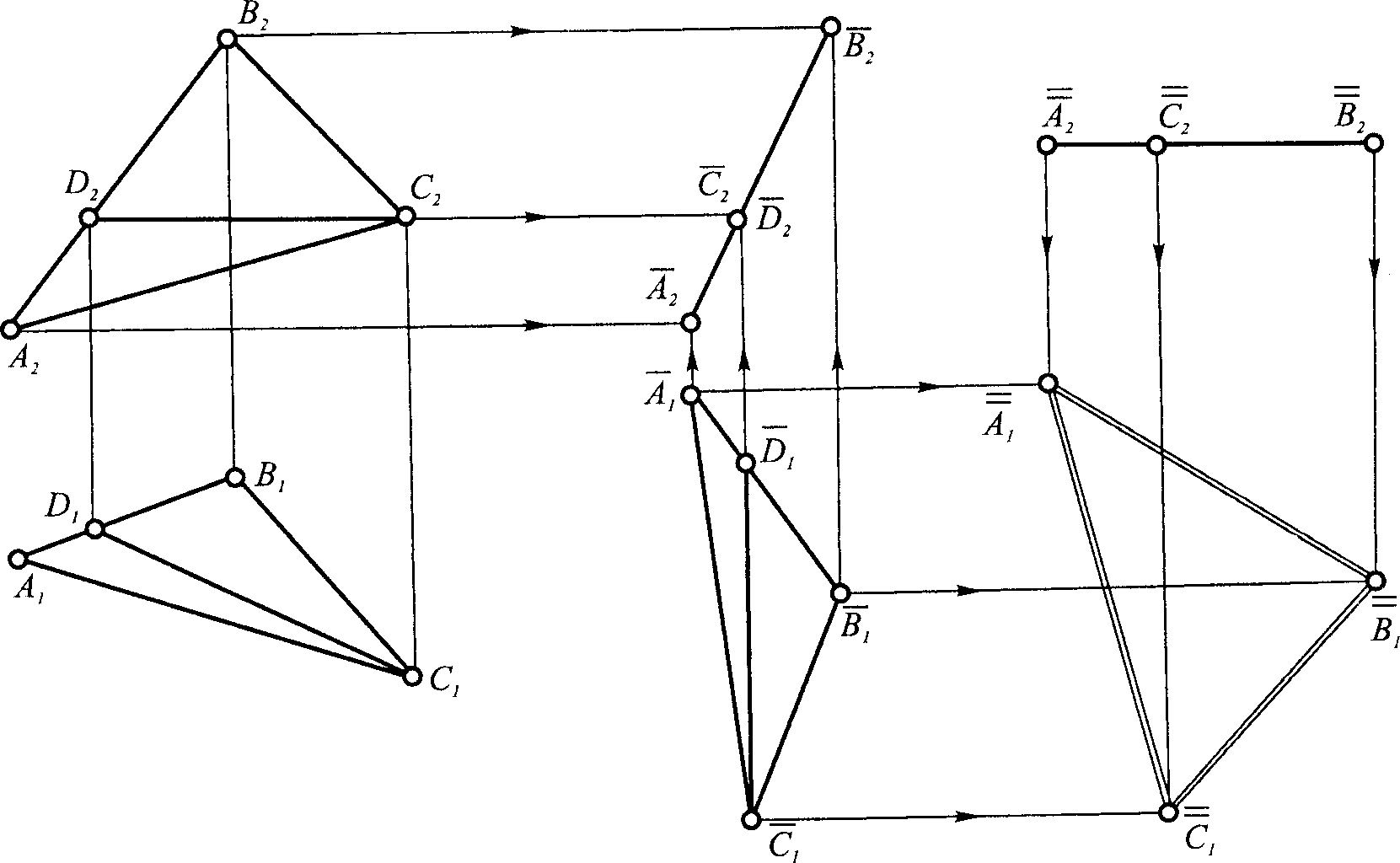
4.2 Навести алгоритм, що застосовують для розв’язання завдань способом плоско-паралельного переміщення стосовно прикладу, що наведений на рисунку 4.2:

Рисунок 4.2 – Визначення дійсної величини трикутника АВС способом плоско-паралельного переміщення

1 Спочатку переміщення всіх точок трикутника відбувались в горизонтальних площинах, поки трикутник АВС не зайняв положення фронтально-проекційної площини (при цьому горизонтальна проекція горизонталі С₁D₁  x₁₂ і горизонтальна проекція трикутника своєї величини на змінила, змінила тільки своє розташування).

2 Наступне переміщення всіх точок трикутника відбувались у фронтальних площинах поки фронтальний слід-проекція трикутника не став паралельним до осі x₁₂.

4.3 Яким чином визначають кількість перетворень проекцій при розв’язуванні конкретних завдань.

Для визначення кількості перетворень проекцій при розв’язуванні конкретних задач необхідно спочатку відобразити такі проекції фігур, за епюром яких можна зразу прочитати ту або іншу властивість за умовою задачі (тобто дати графічну відповідь перетвореним проекціям фігури). При цьому, якщо величини проекцій фігури на цьому епюрі змінюються на двох проекціях одночасно, необхідно виконати два перетворення, на одній проекції – одне перетворення.

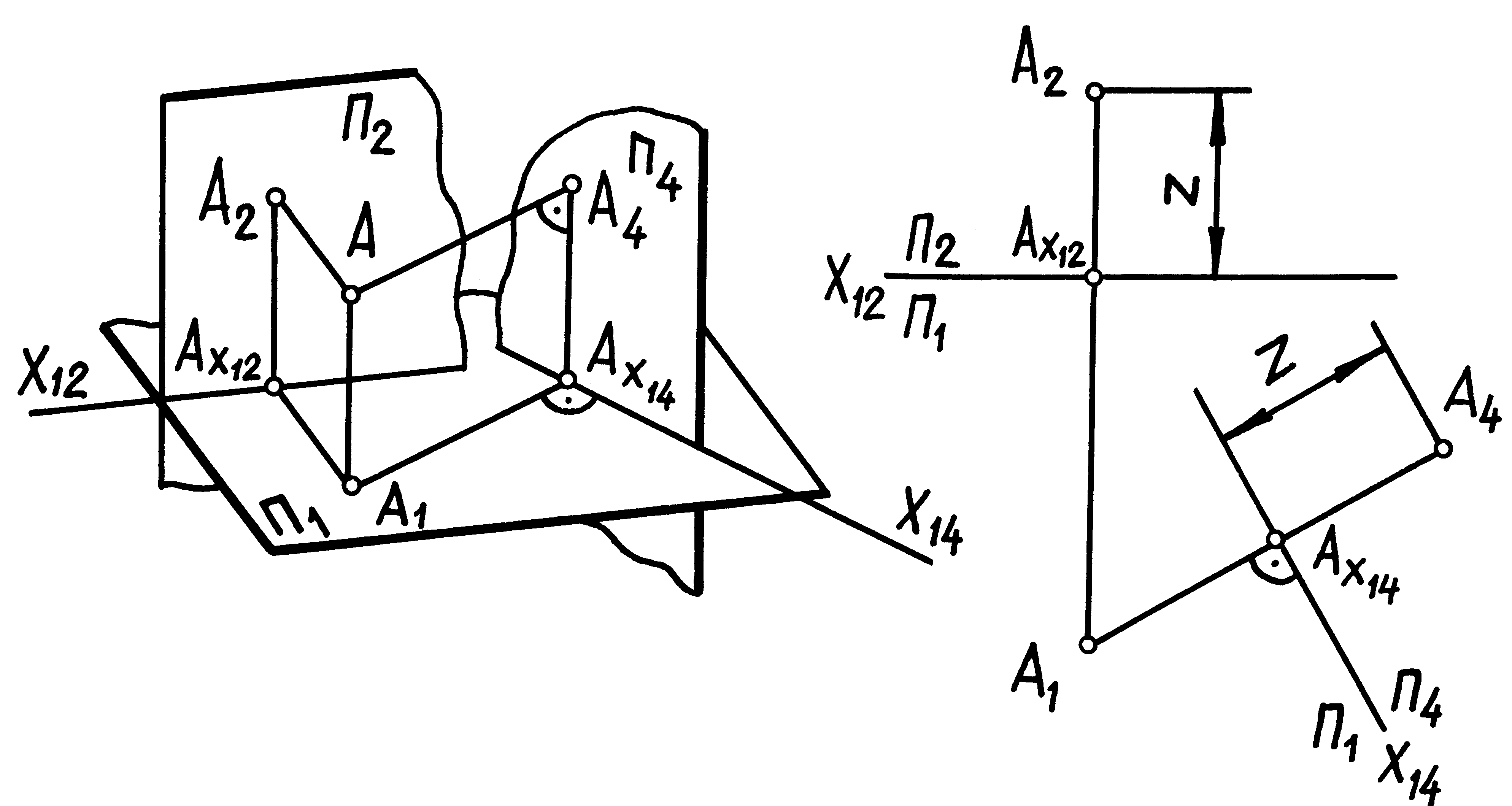
4.4 У чому полягає суть перетворення проекцій через заміну площин проекцій (рисунок 4.3)?

Суть перетворення проекцій через заміну площин полягає в тому, що при незмінному положенні фігури у просторі одна із площин проекцій замінюється на нову таким чином, щоб:

Рисунок 4.3 – Суть способу заміни площин проекцій

1) нова площина проекцій була би перпендикулярною до однієї із незмінних площин проекцій;

2) по відношенню до утвореної нової системи площин проекцій фігура опинилась би у особливому положенні. При цьому: віддаль точок фігури до незмінної площини проекцій у новій і у старій системах площин проекцій залишаються однаковими.

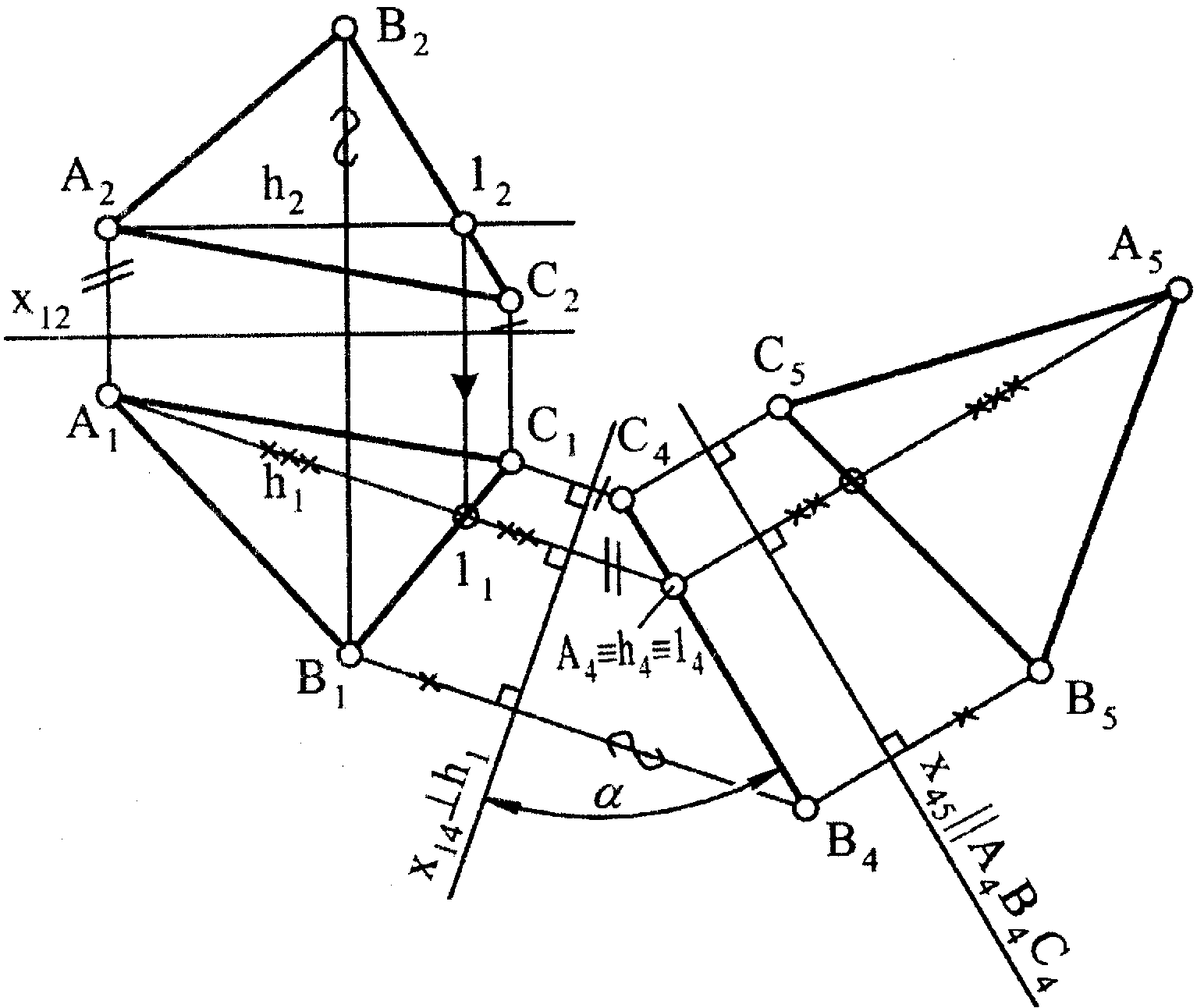
4.5 Поясніть за рисунком 4.4 процес знаходження натуральної величини трикутника АВС за допомогою способу заміни площин проекцій.

1) спочатку перетворюють площину до положення проекційної, коли одна проекція вироджується у пряму, а інша – не змінює своєї величини, змінюється тільки її положення; для цього у площині визначають пряму рівня (наприклад, горизонталь) і відносно неї замінюють одну із заданих площин проекцій на нову, перпендикулярну до прямої рівня площини;

2) потім перетворюють змінену проекційну площину до положення площини рівня; при цьому вироджена проекція площини – пряма лінія займає положення, що паралельне до нової осі проекцій, а інша – збільшується до дійсної величини.

4.6 Які основні чотири перетворення виконуються в процесі розв’язування позиційних і метричних задач?

1 Пряму загального положення перетворюють до положення прямої рівня.

2 Пряму загального положення перетворюють до положення проекційної прямої.

3 Площину загального положення перетворюють до положення проекційної площини.

4 Площину загального положення перетворюють до положення площини рівня.

Рисунок .4.4 – Визначення натуральної величини трикутника способом заміни площин проекцій