Тема 3. Основи інтегрального числення

3.1. Функція F(x) називається первісною для функції f(x), якщо вона задовольняє умові:

1. ;

2. ;

3. ;

4. .

3.2. Що називається невизначеним інтегралом:

1. функція F (x), що має функцію f(x) своєю похідною, або f(x) dx – своїм диференціалом;

2. сукупність всіх первісних функцій для диференціалу f (x) dx;

3. сукупність всіх диференціалів функції F (x);

4. функція f(x), що є плавною зростаючою функцією, диференціал якої F(х)dx.

3.3. Які вирази правильно визначають основні властивості невизначеного інтегралу?

1. ;

2. ;

3. ;

5. .

3.4. Виберіть правильні вирази:

1. ; _;

2. _{; ;}

4. ;

5. ;

3.5. Безпосереднє інтегрування – це знаходження первісної з використанням…

1. властивостей невизначеного інтегралу і таблиць інтегралів;

2. переходу до іншої змінної інтегрування і спрощення підінтегрального виразу до суми інтегралів;

3. спрощення підінтегрального виразу за допомогою властивостей інтегралів і таблиць похідних.

3.6. Метод інтегрування частинами ґрунтується на використанні співвідношення:

1. ;

2. ;

3. ;

4. .

3.7. З геометричної точки зору невизначений інтеграл це

1. площа криволінійної трапеції обмежена графіком функції f(x);

2. набір парабол F(x), які відрізняються чисельним значенням сталої інтегрування С;

3. набір гіпербол F(x), які відрізняються чисельним значенням сталої інтегрування С;

4. набір кривих F(x), які відрізняються чисельним значенням сталої інтегрування С.

3.8. Виберіть вираз, що правильно визначає інтегральну суму:

1. ;

3. ;

4. ;

3.9. Яке рівняння правильно описує визначений інтеграл ?

1. ;

2. ;

3. ;

4. ;

5. .

3.10. Які рівняння правильно виражають властивості визначеного інтегралу?

1. ; , ;

2. ; , ;

3. , , ;

4. ; ; .

3.11. В чому полягає геометричний зміст визначеного інтегралу ?

1. В тому, що він чисельно рівний тангенсу кута нахилу дотичної в даний точці графіка.

2. В тому, що він рівний швидкості зростання функції.

3. В тому, що він чисельно рівний приросту ординати дотичної.

4. В тому, що він чисельно рівний площі криволінійної трапеції, обмеженої графіком функції, віссю абсцис і прямими х = а, х = b.

3.12. Числове значення визначеного інтегралу підраховується за формулою

1. ;

2. ;

3.13. Власним називають інтеграл, якщо

1. підінтегральна функція f(x) неперервна на відрізку [а, b] ;

2. підінтегральна функція f(x) обмежена і неперервна на відрізку [а, b] для як завгодно великих значеннях а і b;

3. підінтегральна функція f(x) обмежена і неперервна на відрізку [а, b] для скінчених значень а і b;

4. підінтегральна функція f(x) обмежена на відрізку [а, b] .

3.14. Формула прямокутників записується як:

1. ;

2. ;

3.15. Формула трапецій записується як:

1. ;

2. ;

3.16. Формула Симпсона записується як:

1. _;

2. ;

3.17. Площа криволінійної фігури обчислюється за формулою:

2. ;

3. .

3.18. Об’єм тіла обертання обчислюється за формулою:

2. ;

3. .

3.19. Довжина кривої, що є графіком функції y = f(x) на відрізку [а ,b]:

3. .

3.20. Обчислити інтеграл :

1. ;

2. ;

3. .

3.21. Обчислити інтеграл :

1. 0.5;

2. 2.5

3. 0;

4. 1;

5. –1.

3.22. Обчислити визначений інтеграл :

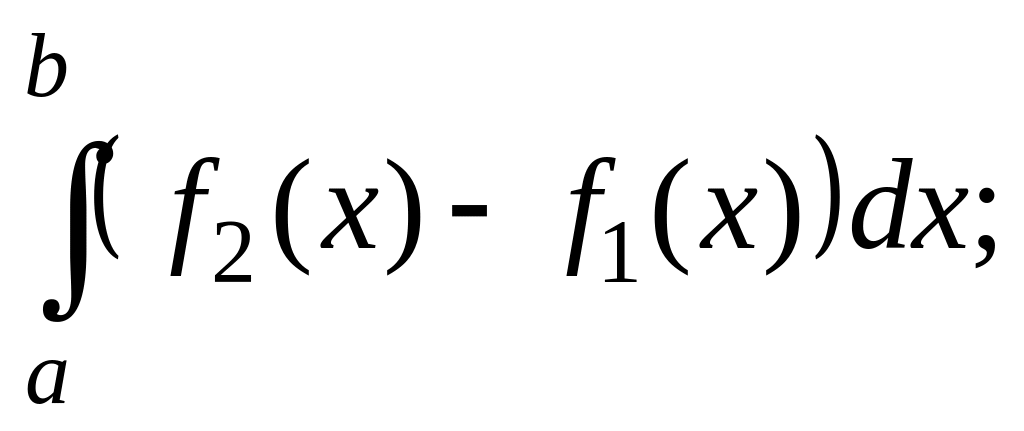
1. ;

2. ;

3. ;

4. ;

5. .