2.1 Жалпы түсінік және айнымалы күштің түрлері

Егер денеге түскен күштердің шамасы немесе бағыты уақытка байланысты өзгеріп отырса, ондай күштерді айнымалы күштер деп атаймыз (2.1.-сурет). Айнымалы күштер өздерінің шамасы мен бағытының өзгеруіне байланысты үш түрге: пульсирлік цикл, симметриялық цикл, айнымалы цикл болып бөлінеді.

2.1-сурет. Кернеулер циклдері.

1. Пульсирлік цикл. Егер күштердің шамасы нольден бастап көбейіп, белгілі бір шамаға жетіп, қайтып нольге түсетін болса, ондай циклді пульсирлік цикл деп атайды. Күш кернеуінің уақыт арқылы байланысын графикпен (2.І.б.г-сурет) көрсетуге болады. Пульсирлік циклде:

σ_min = 0

σ_max = σ_max (1.7)

(1.9)

σ_m – кернеудің орташа шамасы;

σ_a – айнымалы кернеудің амплитудасы.

Ең аз күш кернеуінің ең көп күш кернеуіне қатынасын асимметрия дәрежесі деп атайды және сол асимметрия дәрежесі күш кернеуінен кейін таңба ретінде белгіленіп, сол күш кернеуі кандай циклде пайда болғанын көрсетеді. Мысалы, пульсирлік цикл үшін асмметрия дәрежесі:

r = 0 (1.10)

олай болса, пульсирлік күш түскенде төзімділік шектері а және т болып белгіленеді.

2. Симметриялық цикл. Мүнда күштердің шамасы да, бағыты да өзгереді. Күштер шамасы нольден бастап белгілі бір өлшемге дейін өсіп, қайтадан нольге дейін төмендеп, одан әрі бағытын да өзгертеді. Күш кері бағытта өзінің бастапқы белгіті өлшеміне дейін өсіп, қайтадан нольге түседі (2.1,б-сурет). Былайша айтқанда күш кернеуі симметриялық циклмен немесе синусоида графигі бойынша өзгереді.

Төзімділік шегі σ_-1, τ_-1 болып белгіленеді.

σ_а = σ_max (2.11)

σ_а = 0

σ_min= – σ_max (2.12)

(2.13)

3. Айнымалы цикл. Күш шамасының кері бағытта өзгеруі кез келген мөлшерде болуы мүмкін (1.6.в, д-сурет). Айнымалы цикл дәрежесі

кез келген кері таңбалы сан болып келеді:

r = - 0,2; r= - 0,3; r = - 0,4 және т.с.с. (1.14)

Айнымалы циклмен өзгеретін күштер көбінесе симметриялық немесе пульсирлік циклге келтіріліп есепке алынады. Сондықган практикада бөлшектерді симметриялық және пульсирлік циклмен түсетін күшке есептейді.

Айнымалы күштер әсер еткенде бөлшектер төзімділік шегі немесе қажу шегі арқылы есептеледі.

Материалдардың төзімділік шегі лабораторияда тәжірибелер жүргізу арқылы анықталады. Бір материалдан жасалған көптеген үлгі дене алып, олардың әр түрлі айнымалы күштерді кдбылдау қабілеттілігін байқаймыз. Ол үшін айнымалы күштердің цикл саны мен

2.2 – сурет. Материалдың төзімділік қисығы

шекті кернеудің байланысын анықтайды (2.2.-сурет).

Ол байланыс айнымалы күштердің цикл саны көбейген сайын үлгі дене мөлшері аз кернеуде істен шығатынын көрсетеді. Былайша айтқанда, айнымалы күштердің цикл санының көбеюінен шекті кернеу азаяды. Мысал үшін N₁=10₃ caнынa σ₁ сәйкес келесе, N₂ = 10⁵санына σ₂ сәйкес келеді және де σ₁ > σ₂. Айнымалы күштердің цикл санын одан әрі көбейте берсек, цикл саны белгілі бір шамадан асқанда шекті кернеу өзгермей бір қалыпты қалады, график бойынша қисық сызық түзу сызықка айналады. Бұл жағдай цикл санын логарифмдік өлшемде көрсеткенде (1.8.-сурет) өте айқын байқалады, сондықтан іс жүзінде көбінесе осы өлшем бойынша материаддардың төзімділік қисығын сызады.

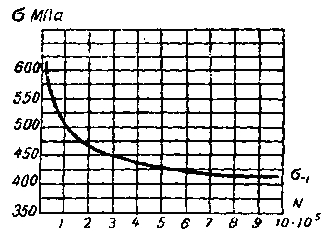
2.2 – сурет. Материалдың төзімділік қисығы

2.3-сурет. Материалдың төзімділік шегі

Сонымен, төзімділік шегі деп материалдардың бұзылмай шексіз көп циклді айнымалы күштерді қабылдауына сәйкес келетін күш кернеуін айтады.

Бөлшектердің 80 пайызы осы материалдардың төзімділік шегінің азаюынан істен шығады, сондықтан қазіргі кезде көптеген бөлшектердің өлшемдері төзімділік шегіне есептеу арқылы табылады. 1.8.-суретте көрсетілген қисық сызықтың формасы материалдарға байланысты болады және сол қисық сызық формуласын жазсақ, жалпы түрде былай көрсетуге болады:

σ^m N= C, 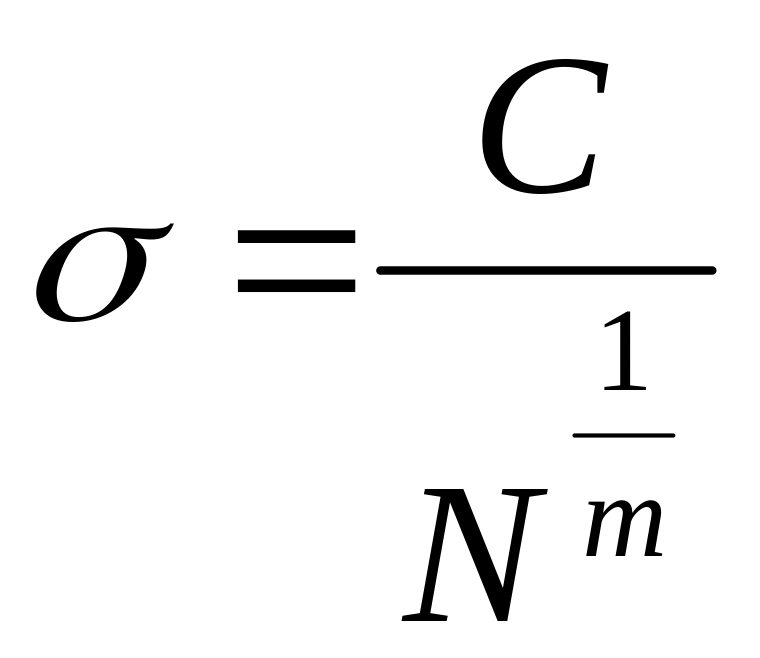(2.15)

m мен С мәндерін σ_-1, N₀ және σ₁, N₁ арқылы табуға болады (1.8.-сурет).

О л үшін:

m – қисық сызықтың негізгі көрсеткіші болып саналады.