Методические рекомендации к выполнению задания 6

Динамика долей рынка может быть объяснена и спрогнозирована, если оценить по каждой марке уровень приверженности и уровень притягательности, которые определяются следующим образом:

Уровень приверженности марке – это процент покупателей, которые, купив марку А в настоящем периоде, продолжают ее покупать и в будущий момент времени.

Уровень притягательности марки – это процент покупателей, кото­рые, купив марку конкурента в настоящем периоде, в будущем периоде намереваются покупать марку А.

Эти уровни характеризуют вероятность перехода покупателей из одного со­стояния в другое. Знание вероятностей переходного состояния позволяет изучить скрытую конкурентную динамику долей рынка, а затем сформулировать на этой основе прогноз предполагаемых изменений позиций марок на рынке в будущих периодах. Доля рынка любой марки в будущем периоде (t + 1) определяется сле­дующим образом:

,

где PM_t, PM_t+1 – доли рынка, удерживаемые маркой, соответственно в данном и будущем периодах;

 – уровень приверженности марке;

 – уровень притягательности марки.

Следует обратить внимание на то, что в таблице 6 пересечение строки и колонки с одной и той же маркой содержит процент покупателей, которые поку­пали данную марку в настоящем периоде t и будут покупать ее в следующем пе­риоде (t + 1). Пересечения же остальных строк с данной колонкой характеризуют проценты потребителей, покупающих в настоящий момент t конкурирующие марки, но которые в следующем периоде (t + 1) намерены покупать данную марку.

При расчете уровня приверженности и уровня притягательности каждой марки следует учитывать, что упомянутые выше проценты имеют неодинаковый вес (они имели бы одинаковый вес только при равенстве долей рынка между марками) и любая средняя величина из этих процентов должна рассчитываться как средневзвешенная с учетом удерживаемых марками долей рынка.

Тема: Информационная система маркетинга и маркетинговые исследования

Задание 7

Для оптимизации плана производства предприятию, выпускающему одежду, необходимо знать, каковы пропорции в численности групп потребителей, имеющих разный рост. Чтобы получить необходимую информацию предприятие провело описательное маркетинговое исследование.

При опросе выборки потребителей каждый из них указал свой рост. Результаты опроса приведены в таблице 7.

Используя результаты опроса,

постройте гистограмму распределения частот, с которыми потребители обследованной выборки указали разные типоразмеры одежды;

рассчитайте показатели среднего значения и стандартного отклонения.

Методические рекомендации к выполнению задания 7

В маркетинговых исследованиях практически всегда возникает необходимость описать наблюдаемые переменные с помощью показателей, резюмирующих информацию.

Показателем центра группирования значений исследуемой переменной (центральной тенденции) является средние арифметическое значение наблюдаемой переменной, которое определяется по формуле:

Таблица 7

Рост респондентов выборки, см.

Респонденты	Вариант
	1	2	3	4	5	6	7	8	9	10
1	172	184	172	178	181	170	178	174	176	162
2	162	174	162	173	171	177	170	204	174	188
3	177	188	177	201	186	176	167	172	156	170
4	188	169	188	169	173	170	167	167	174	197
5	187	162	187	189	192	184	177	170	181	168
6	192	160	192	177	189	176	173	163	186	183
7	153	173	181	177	182	192	183	183	184	166
8	178	177	173	177	181	190	189	167	177	190
9	182	169	186	173	175	173	173	180	178	180
10	164	175	164	174	174	181	181	192	182	174
11	167	174	168	181	180	189	182	171	168	156
12	158	175	168	189	178	161	173	173	176	178
13	157	153	178	177	183	178	189	185	173	154
14	165	179	165	172	170	170	177	185	187	176
15	167	169	177	172	171	183	178	174	182	163
16	174	169	164	186	189	183	171	174	178	190
17	169	179	182	181	169	176	166	173	164	158
18	171	175	171	195	185	172	182	189	165	171
19	176	173	176	164	179	169	166	180	172	178
20	171	172	171	194	198	178	191	178	173	183
21	172	170	172	158	179	177	183	176	173	186
22	171	160	171	186	175	187	176	178	162	186
23	184	160	178	176	180	188	186	177	166	170
24	174	191	174	165	175	183	179	168	194	169
25	176	183	173	179	168	176	175	181	165	174
26	170	174	170	166	178	183	181	175	155	162
27	195	184	185	182	157	171	176	159	187	182
28	184	177	184	182	188	172	165	161	174	184
29	199	174	179	165	163	178	162	196	150	173
30	168	180	168	171	178	160	174	173	164	168

г ,

де X_i – наблюдаемые в выборке значения переменной;

n – количество наблюдений в выборке.

Для описания случайной переменной лишь один расчет среднего значения является недостаточным. Он должен сопровождаться расчетом показателей степени вариации (рассеивания) значений случайной величины. К ним можно отнести следующие:

диапазон наблюдаемых значений (X_min, x_max);

стандартное отклонение (классический показатель рассеивания случайной величины);

коэффициент вариации.

Формула расчета выборочного стандартного отклонения имеет вид:

.

Стандартное отклонение является удобным и естественным показателем рассеивания значений переменной в силу соответствия единиц его измерения с единицами измерения ее значений.

Коэффициент вариации () используется в тех случаях, когда степень рассеивания более естественно описывать, сопоставляя ее со средним значением и рассчитывается по формуле:

.

Каждая из перечисленных выше характеристик степени рассеивания дает представление о том, как сильно могут отклоняться от своего центра группиро­вания значения исследуемой случайной величины. Если говорить о графических формах представления распределения частот исследуемого признака, то для этого обычно используется специальная диаграмма, называемая гистограммой.

Пример гистограммы приведен на рис. 2.

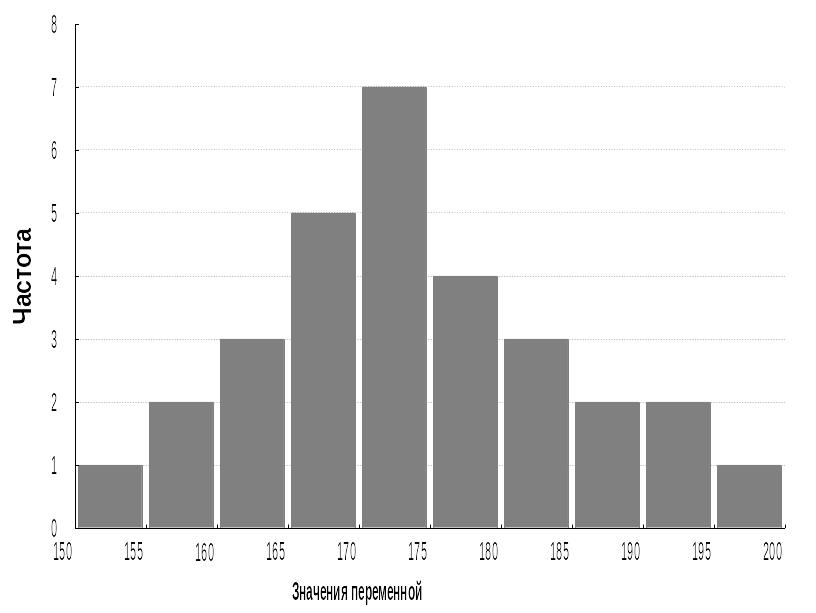
Рис. 2 – Пример гистограммы

Для построения гистограммы весь диапазон наблюдаемых в выборке значений случайной переменной (от минимального до максимального наблюдаемого значения) разбивается на несколько равных интервалов. Затем определяется количество наблюдаемых в выборке значений переменной, «попадающих» в каждый интервал. На основе подсчитанных таким образом частот, с которыми встречаются разные наблюдаемые значения переменной, строится диаграмма.

По оси 0Х откладываются значения границ интервалов. По оси 0Y –частоты, с которыми отдельные значения переменной «попадают» в каждый из интервалов.

Задание 8

Предприятию, выпускающему одежду, необходимо знать, существует ли зависимость между ростом человека и размером одежды, которую он носит. Чтобы получить необходимую информацию оно провело опрос, в ходе которого каждый респондент указал свой рост и размер одежды. Результаты опроса приведены в таблице 8.

Таблица 8

Значения роста и размера одежды, указанные респондентами

Респондент	Вариант
	1		2		3		4		5
1	172	48	172	46	181	48	178	50	176	48
2	162	46	162	46	171	48	170	48	174	50
3	177	50	177	48	186	48	167	50	183	52
4	188	56	188	54	173	48	167	50	174	50
5	187	52	187	52	192	56	177	48	179	52
6	192	52	192	54	189	54	173	48	186	48
7	153	46	181	48	182	50	183	48	184	54
8	178	50	173	48	181	50	189	52	177	50
9	182	48	186	50	175	52	173	50	178	50
10	164	46	164	46	174	48	162	46	176	48
11	167	48	168	46	180	52	163	46	168	48
12	158	48	168	48	178	48	173	48	176	54
13	157	46	178	50	183	52	189	52	173	52
14	165	48	165	48	170	46	177	50	187	50
15	167	48	177	50	171	48	178	50	182	50
16	174	52	164	50	189	54	171	48	178	48
17	169	50	182	48	169	48	166	48	167	48
18	171	48	171	46	185	54	182	52	165	46
19	176	48	176	48	179	48	166	48	172	48
20	171	50	171	46	198	52	165	48	185	54
21	172	50	172	48	179	48	183	54	183	50
22	171	48	171	48	175	54	176	48	169	52
23	184	52	178	50	180	54	186	56	166	48
24	174	52	174	50	175	48	174	52	194	52
25	176	48	173	50	168	50	175	52	167	48
26	170	50	170	50	178	46	165	46	174	50
27	195	54	185	52	157	48	176	54	187	52
28	184	52	184	54	188	50	165	48	184	52
29	199	56	179	52	163	46	162	46	173	54
30	168	48	168	50	178	46	174	50	164	46

Проанализируйте данные таблицы 8 и дайте ответ на следующие вопросы:

существует ли взаимозависимость между ростом человека и размером одежды, которую он носит?

если связь существует, то каков характер этой связи?