
- •Вектором – , противоположным вектору 0 называется вектор, имеющий ту же длину, что и , но противоположно направленный.
- •Скалярное произведение векторов
- •Преобразование векторов. Умножение матрицы на вектор
- •Задания для самостоятельного решения
- •Элементы векторной алгебры II
- •Алгоритм 7
- •Задания для самостоятельного решения
- •Функции и их графики
- •Основные способы задания (определения) функций
- •Классификация элементарных функций по л. Эйлеру
- •Задания для самостоятельной работы

а б в
Рис. 7.2
тора
![]() называется длина отрезка АВ.
Два вектора равны,
если они коллинеарны, сонаправлены и
их длины равны.
называется длина отрезка АВ.
Два вектора равны,
если они коллинеарны, сонаправлены и
их длины равны.
Это определение позволяет:
отождествлять геометрический вектор с параллельным сдвигом пространства R3;
считать, что все равные векторы (например,
 )
можно
отождествлять с вектором
)
можно
отождествлять с вектором
 (рис. 7.2, в),
имеющим началом точку О –
начало координат. Вектор
называется радиус-вектором,
причем он задается только одним
параметром – своим концом.
(рис. 7.2, в),
имеющим началом точку О –
начало координат. Вектор
называется радиус-вектором,
причем он задается только одним
параметром – своим концом.
Линейными операциями над векторами являются: сложение векторов и умножение векторов на действительные числа. Определение этих операций при различных способах задания векторов представлены в табл. 7.1.
Вектором – , противоположным вектору 0 называется вектор, имеющий ту же длину, что и , но противоположно направленный.
Свойства операции сложения векторов.
+
 =
+
(коммутативность
сложения).
=
+
(коммутативность
сложения).(
 )+
)+ =
+
(
+
)
(ассоциативность сложения).
=
+
(
+
)
(ассоциативность сложения). =
(свойство нуля).
=
(свойство нуля).+(– )=
 (свойство противоположного элемента).
(свойство противоположного элемента).
Отметим, что операция сложения векторов обладает всеми свойствами сложения действительных чисел.
Разностью – векторов и называется по определению вектор +(- ).
Свойства операции умножения вектора на число.
1· = (унитарность).
 (ассоциативность)
(ассоциативность)
Т а б л и ц а 7.1
Вид операции |
Способ задания векторов |
||
Геометрический
|
Аналитический
|
Пример |
|
1. Сложение
векторов
|
а) Правило параллелограмма
б) Правило треугольника
|
|
|
2. Умножение
вектора на число:
|
|
|
|
 (дистрибутивность
сложения векторов относительно умножения
на число).
(дистрибутивность
сложения векторов относительно умножения
на число). (дистрибутивность
сложения чисел относительно умножения
векторов на числа).
(дистрибутивность
сложения чисел относительно умножения
векторов на числа).
Если вектор
≠0,
то вектор
![]() –
орт, т. е. единичный вектор, сонаправленный
с вектором
.
–
орт, т. е. единичный вектор, сонаправленный
с вектором
.
Если два вектора и коллинеарны, то всегда существует такое число λ R, что = λ , это число λ называется отношением коллинеарных векторов.
Декартовы прямоугольные системы координат позволяют арифметизировать геометрию, рассматривая вместо геометрических векторов тройки чисел. Этот подход восходит к Декарту, называется координатным и позволяет упростить решения задач, связанных с векторами.
Проекцией
вектора
![]() на ось (направленную прямую) l
называется произведение длины вектора
на косинус угла между вектором
и осью l:
на ось (направленную прямую) l
называется произведение длины вектора
на косинус угла между вектором
и осью l:
![]() .
.

Рис. 7.3
Для любых трех точек пространства и любой оси можно показать справедливость формул:
Прl
 =
Прl
+
Прl
=
Прl
+
Прl

Прl λ ( ) = λ Прl
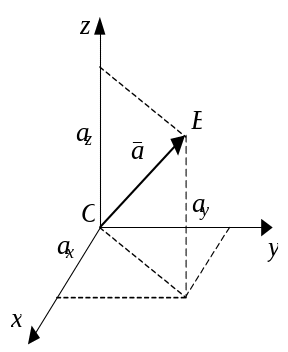
Под координатами вектора = в декартовой прямоугольной системе координат (ДСК) понимается упорядоченная тройка чисел (Прох , Проy , Проz ). Если точки А и В в фиксированной ДСК имеют координаты (х0, y0, z0) и (х1, y1, z1) соответственно, то вектор в этой системе координат имеет координаты (х1 – х0, y1 –y0, z1 – z0). В частности, если х0 = y0 = z0 = 0 (начало вектора совпадает с началом координат), то
Рис.
7.4
![]() =.(х1 – 0, y1
– 0, z1 –
0) =
=.(х1 – 0, y1
– 0, z1 –
0) =
= (х1, y1, z1).
Введем обозначения для координат вектора (рис. 7.4):
Прох = ах, Проy = ау, Проz = аz.
Если
![]() ,
, ![]() ,
, ![]() –единичные
векторы (орты) осей ДСК, то вектор
единственным
образом может быть представлен в виде:
–единичные
векторы (орты) осей ДСК, то вектор
единственным
образом может быть представлен в виде:
![]()
или
![]() .
.
Возможность представить любой вектор из R3 упорядоченной тройкой чисел позволяет все операции с векторами представить в координатной форме.
Если
![]() ,
,
![]() и
λ
R,
то
и
λ
R,
то
= ах = вх , ау = ву , аz = вz ;
װ
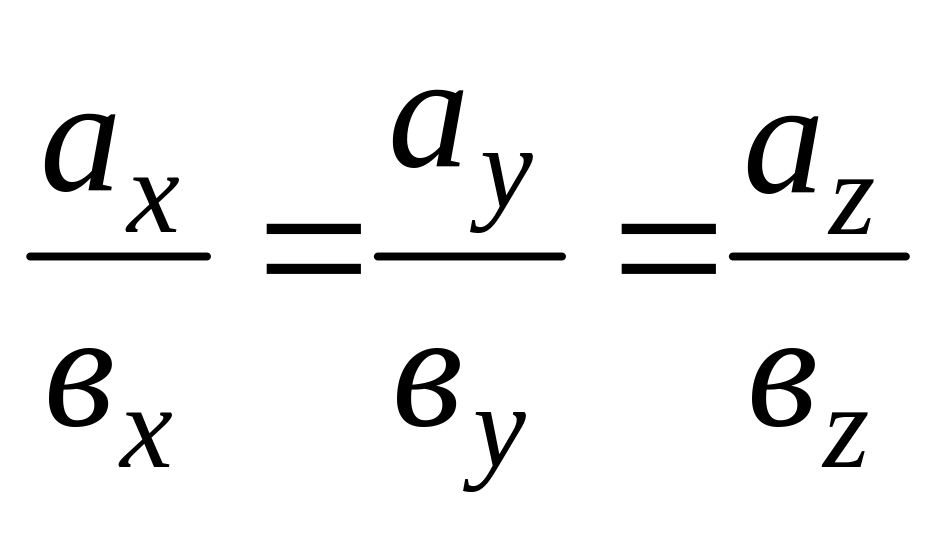 ;
; ;
;λ
 ;
;+ = (ах +вх , ау + ву , аz + вz) .
Пример 7.1. 1) Построить на плоскости точки А(0, –1), В(–1, –3), С(–2, 1);
2) Найти координаты
векторов
![]() и построить их. Убедиться, что
и построить их. Убедиться, что
![]() ;
;
3) Построить вектор
![]() и найти координаты точки D.
Является ли вектор
и найти координаты точки D.
Является ли вектор
![]() ?
?
4) Построить вектор
![]() и найти его координаты;
и найти его координаты;
5) Является ли
вектор
![]() коллинеарным
вектору
?
коллинеарным
вектору
?
6) Привести примеры двух векторов, коллинеарных вектору .
Ответы:
2)
![]() ;
;
3)
![]() D(2,3),
да. 4)
(0, 6) 5)
нет
D(2,3),
да. 4)
(0, 6) 5)
нет
6) например, (1, 2); (3, 6)
Пример 7.2.
Даны точки
![]()
![]()
![]()
![]() .
.
Найти координаты векторов
 .
.Является ли их четырехугольник ABCD параллелограммом?
Ответы:
1)
![]() ;
;
2) нет, так как
![]() а
а
![]()
.
.








