ЛАБОРАТОРНЫЕ РАБОТЫ ПО ДИСЦИПЛИНЕ:
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ НГО. МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
(Разработал: Катанов Юрий Евгеньевич)
Лабораторная работа №1
Цель: Построение линии тренда на основе метода наименьших квадратов (стандартная постановка задачи, точечный МНК, линейные и квадратичные модели)
Задача
1.
Для
линейной модели значений
и
,
методом наименьших квадратов в стандартной
постановке задачи построить линию
тренда, прогнозирующую дальнейшую
совокупность исходных значений.
Оценить
точность решение при
Сделать проверку соответствия значений.
Построить линию тренда.
Для примерной таблицы значений, находим следующие составляющие:
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,5 |
4,3 |
6,8 |
9,0 |
10,3 |
12,7 |
Решение: находим следующие составляющие:
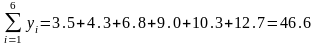
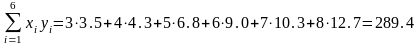
Записываем систему
Или
Выражая
из второго уравнения
Подставляя полученное выражение в первое, получим
Тогда
Следовательно, искомое уравнение линии тренда примет вид:
Теперь оценим точность данного решения:
В
условиях этого примера имеем
.
Тогда
Таким образом, подставляя в последнее выражение исходные значения исходной таблицы, можно оценить, насколько данные величины отклонены от построенной линии тренда.
Задача 2. Точечным методов наименьших квадратов аппроксимировать заданную таблицу линейным и квадратичным полиномами.
xi |
3 |
4 |
4 |
5 |
yi |
5 |
8 |
7 |
6 |
Решение: для линейного полинома
,
т.е.
.
Матрица
Ф принимает вид:
Вектор
наблюдений y
выглядит следующим образом:
.
Тогда
,
.
Решая
систему
,
получаем вектор искомых коэффициентов
,
,
Выражая
из второго уравнения
,
и подставляя его в первое, имеем:
,
,
,
.
Тогда
.
Таким
образом, вектор искомых значений
принимает вид
,
значит искомый полином представляется
как
Оценим погрешность такой аппроксимации:
.
Для квадратичного полинома имеем следующее:
т.е.
.
Матрица Ф принимает вид:
.
Вектор наблюдений y остается без изменений .
Тогда
,
.
Решая систему , получаем вектор искомых коэффициентов
,
или представляя ее в виде системы
уравнений:
Поскольку данная система является квадратной (т.е. число неизвестных равно числу уравнений), то, например, решим ее с помощью метода Крамера.
Тогда
.
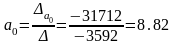
Таким
образом, вектор искомых значений
принимает вид
,
значит искомый полином представляется
как
.
Оценим погрешность такой аппроксимации:
,
Следовательно, сравнивая ошибки прогноза для линейного и квадратичного полиномов, в данной случае, предпочтительнее будет линейный полином.
Кроме того, если значения величин значительно отличаются друг от друга, то необходимо использовать квадратичный полином, если различия между ними не существенны - то линейный.
Варианты заданий
1 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,7 |
4,1 |
6,3 |
9,3 |
10,1 |
12,4 |
2 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
2,5 |
3,3 |
5,8 |
8,0 |
9,3 |
11,7 |
3 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,9 |
4,7 |
6,9 |
9,2 |
10,5 |
12,4 |
4 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,1 |
4,5 |
6,4 |
9,2 |
10,8 |
12,2 |
5 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,0 |
4,1 |
6,2 |
9,5 |
10,1 |
12,0 |
6 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,8 |
4,3 |
6,3 |
9,0 |
10,4 |
12,2 |
7 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,1 |
4,9 |
6,3 |
9,7 |
10,1 |
12,2 |
8 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,4 |
4,7 |
6,9 |
9,3 |
10,0 |
12,5 |
9 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,1 |
4,3 |
6,7 |
9,0 |
10,5 |
12,6 |
10 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,4 |
4,0 |
6,5 |
9,2 |
10,9 |
12,2 |
11 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,8 |
4,4 |
6,2 |
9,7 |
10,6 |
12,1 |
12 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,4 |
4,6 |
6,3 |
9,0 |
10,2 |
12,3 |
13 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,0 |
4,1 |
6,2 |
9,0 |
10,2 |
12,5 |
14 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,4 |
4,2 |
6,0 |
9,0 |
10,1 |
12,0 |
15 вариант
|
3 |
4 |
5 |
6 |
7 |
8 |
|
3,0 |
4,1 |
6,2 |
9,0 |
10,1 |
12,2 |