4.2. Расчет политропных процессов идеального газа

Расчет термодинамических процессов включает

1. вычисление термодинамических параметров системы в начальном и конечном состояниях;

2. вычисление количеств работы изменения объема 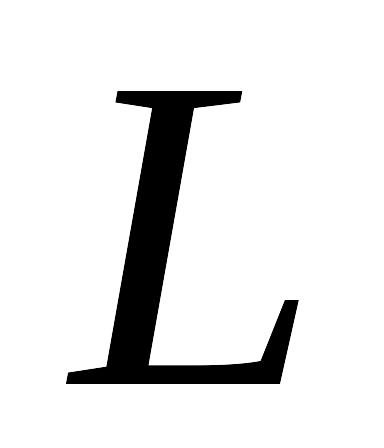, полезной внешней работы 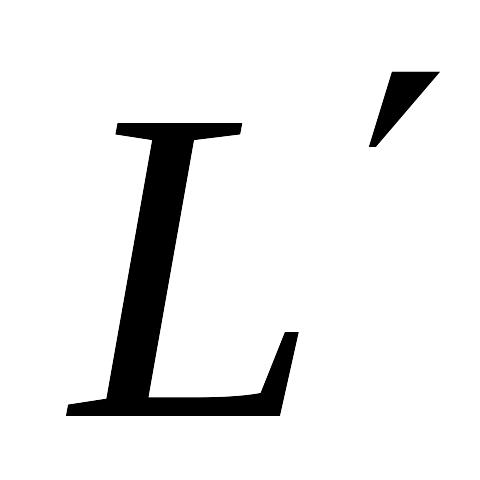и теплоты в процессе;

3. вычисление изменения внутренней энергии , энтальпии и энтропии 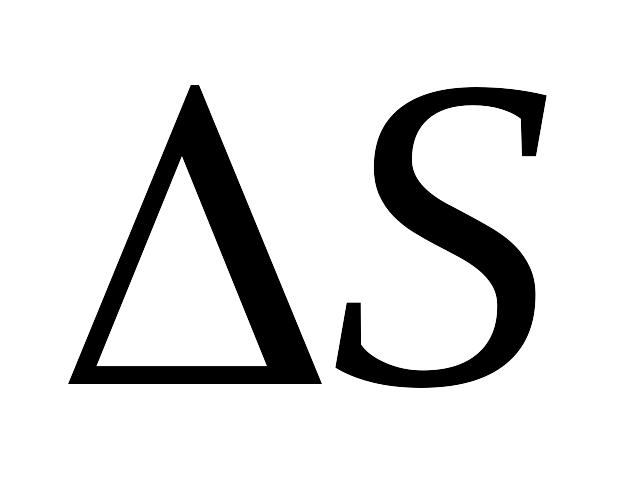в процессе;

4. графическое изображение процесса в термодинамических диаграммах .

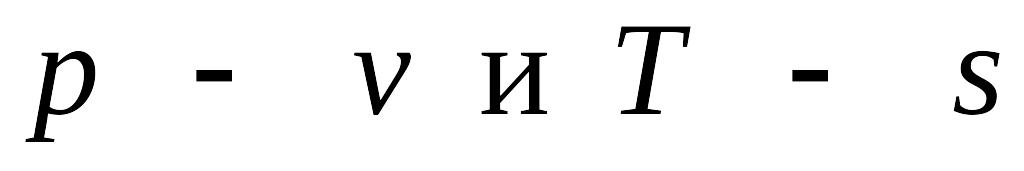Из уравнения политропного процесса и состояния идеального газа можно получить соотношения между параметрами в политропном процессе:

.

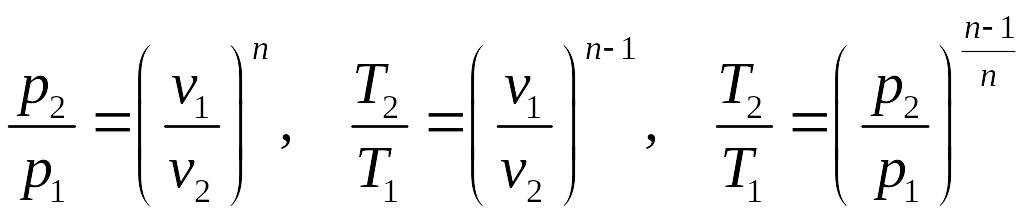Количество теплоты в политропном процессе

.

Работа изменения объема в политропном процессе может быть найдена интегрированием выражения для работы:

.

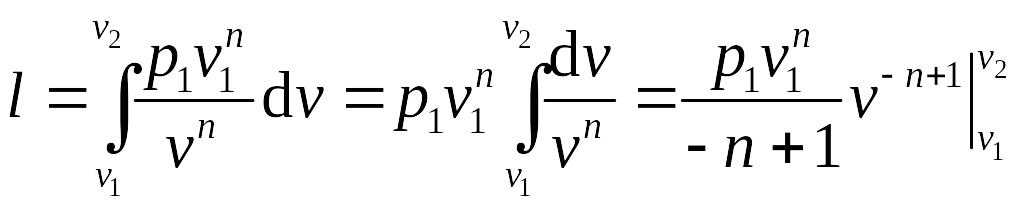использование соотношений между параметрами в политропном процессе позволяет записать выражение для удельной работы изменения объема в трех эквивалентных формах:

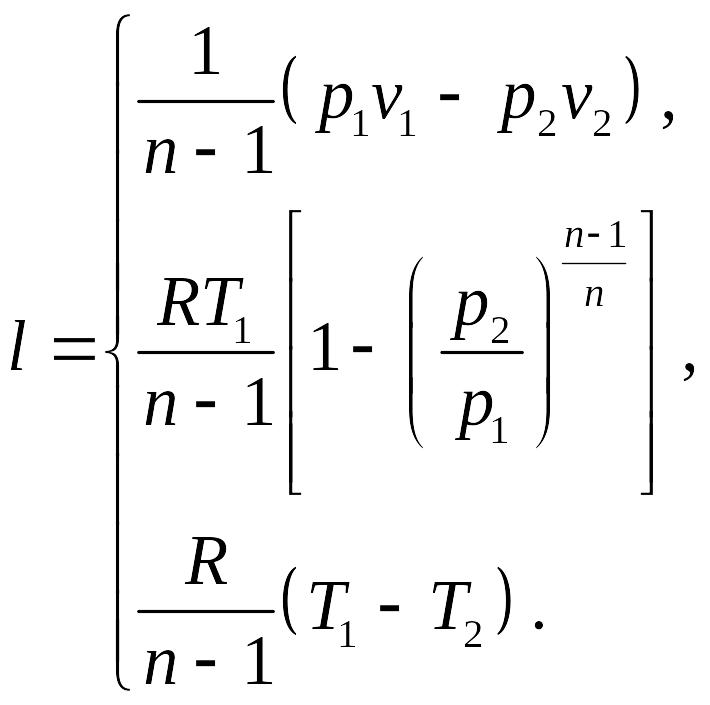
Полезная внешняя работа также может быть вычислена, приняв во внимание тот факт, что

.

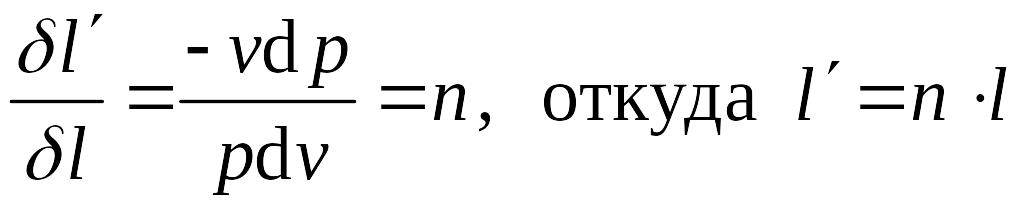Лекция 8

4.3. Частные случаи политропных процессов

Как следует из определения показателя политропы, он может принимать значения от –∞ до +∞. Чаще всего на практике имеют дело с четырьмя частными случаями политропных процессов.

Изохорный процесс

По определению изохорным (изохорическим) процессом называется процесс, в течение которого поддерживается постоянным объем системы, т.е. уравнение изохорного процесса можно записать в виде

.

Показатель политропы для изохорного процесса может быть найден из уравнения политропного процесса:

, .

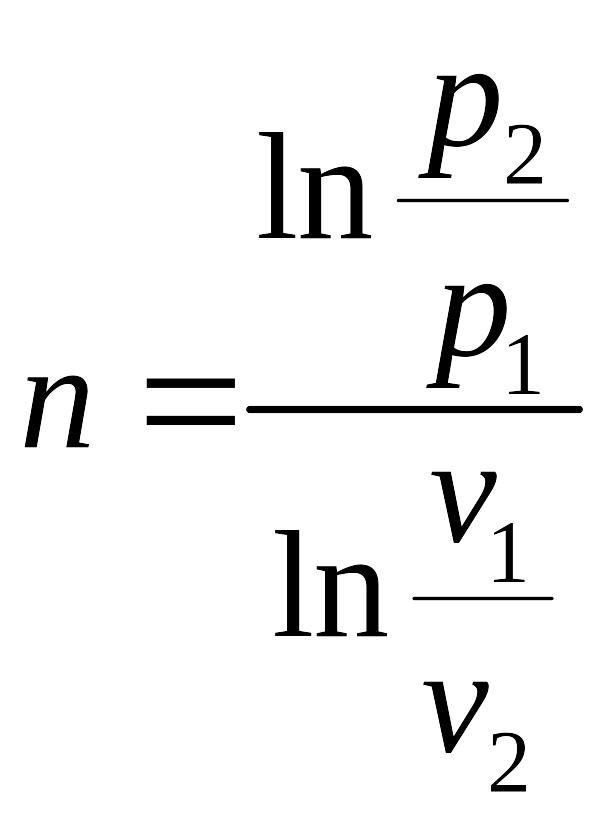Тогда термодинамический расчет изохорного процесса сведется к использованию формул для политропного процесса, в которых :

.

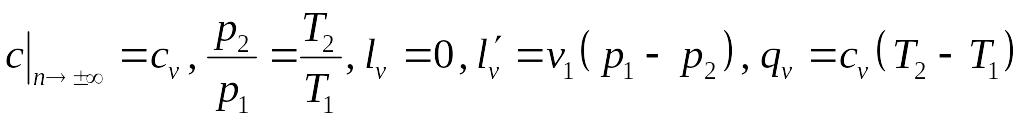И зображение изохорного процесса в термодинамических диаграммах показано на рис.3.1.

Изобарный процесс

Изобарным (изобарическим) называется процесс при постоянном давлении, т.е. . Показатель политропы изобарного процесса: . Тогда, полагая во всех формулах для политропного процесса , получаем

.

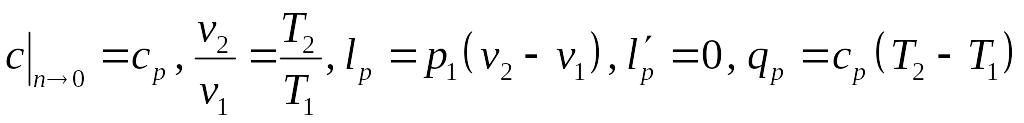
На рис.3.2 изображен изобарный процесс в термодинамических диаграммах.

На диаграмме пунктиром показан также изохорный процесс, который изображается экспоненциальной кривой бόльшей крутизны, что следует из сравнения производных

.

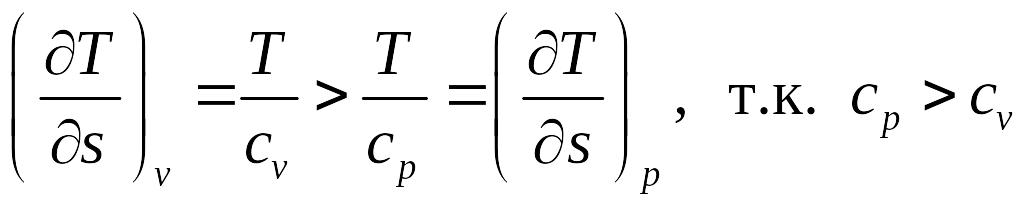Изотермический процесс

Изотермическим называется процесс, в котором поддерживается постоянной температура системы: .

Показатель политропы изотермического процесса для идеального газа будет равен 1, n = 1.

Теплоемкость изотермического процесса оказывается равной бесконечности, что приводит к неопределенности типа при вычислении количества теплоты в изотермическом процессе по стандартной формуле, которая устраняется при использовании I закона термодинамики:

,

откуда для изотермического процесса идеального газа

.

Работа изменения объема в изотермическом процессе (или полезная внешняя работа) может быть вычислена по определению работы, в котором давление выражено через удельный объем из уравнения состояния идеального газа:

.

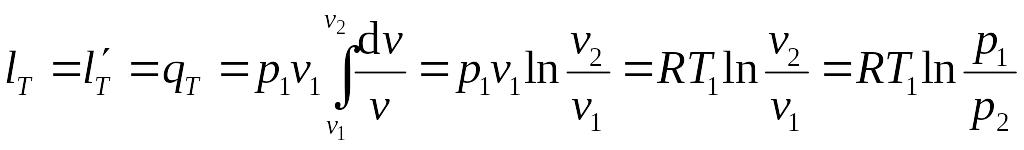Изменение энтропии в изотермическом процессе находится из определения:

.

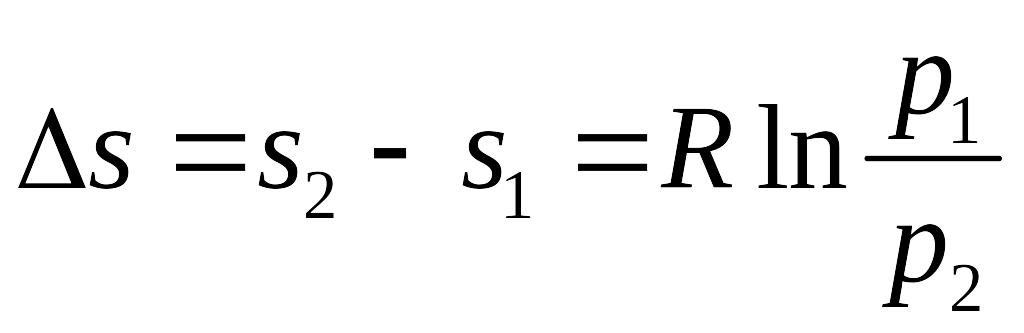В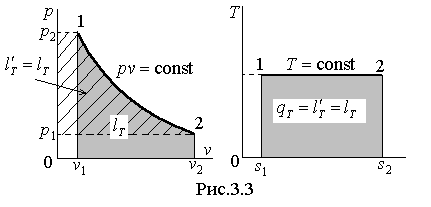 координатах p – v изотермический процесс изображается равнобочной гиперболой, а в T – s – горизонтальной прямой T=const (рис.3.3).

Адиабатический процесс

По определению адиабатическим (адиабатным) процессом называется процесс без теплообмена, т.е. . Тогда теплоемкость адиабатного процесса равна нулю (с_ад=0) и в обратимом адиабатическом процессе остается постоянной энтропия, т.е. уравнение адиабатического процесса может быть записано в виде .

Из определения теплоемкости политропного процесса находим значение показателя политропы для адиабатического процесса:

.

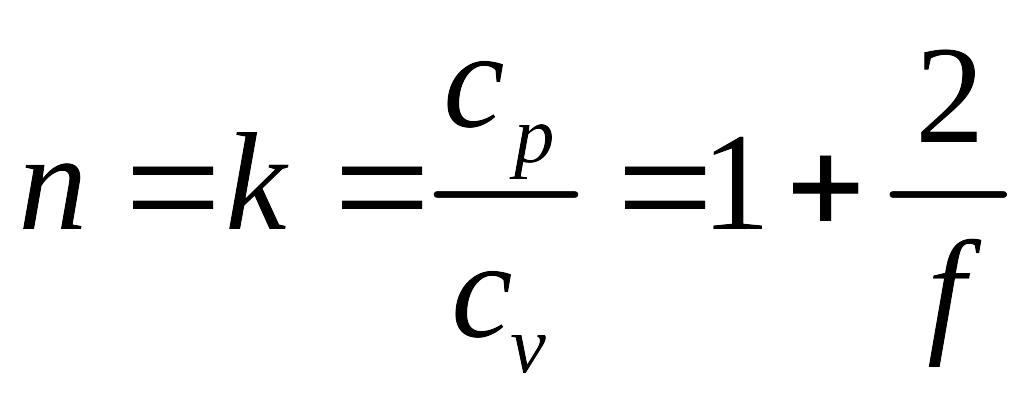В переменных (p,v) уравнение адиабатного процесса имеет вид

.

Работа в адиабатном процессе, как следует из I начала термодинамики, осуществляется за счет уменьшения внутренней энергии системы и вычисляется по формулам для работы политропного процесса с заменой n→k:

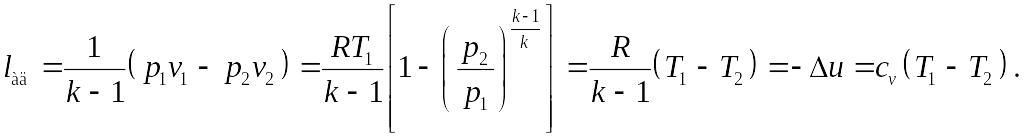
Полезная внешняя работа адиабатического процесса в k раз больше работы изменения объема и совершается за счет уменьшения энтальпии системы:

.

И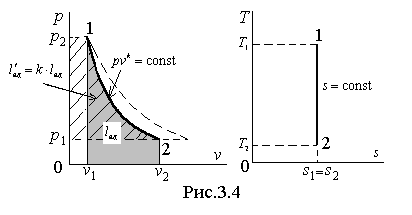 зображение обратимого адиабатического процесса в термодинамических диаграммах показано на рис.3.4.

Пунктирной линией на диаграмме p – v показан изотермический процесс, который изображается более пологой, чем адиабата кривой. В самом деле, сравнивая производные от давления по объему для адиабаты и изотермы, получаем

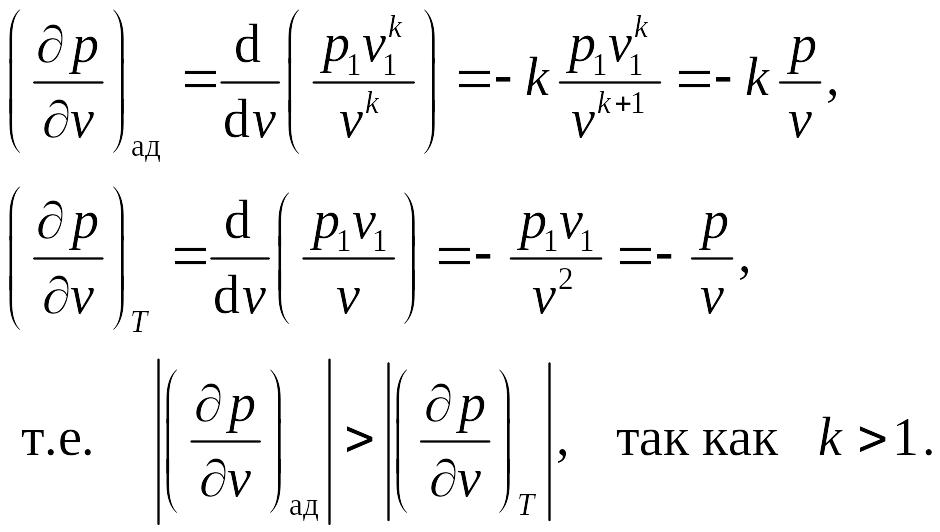
Обобщающее значение политропного процесса

Изобразим в диаграммах рассмотренные выше четыре частных процесса (рис.3.5), проходящих через какое-либо одно состояние. Все они описываются одной степенной функцией вида , где показатель политропы n и вместе с ним теплоемкость процесса c принимают конкретные значения, которые приведены в табл.1.

Таблица1

Характеристики политропного процесса

Процесс	Уравнение процесса	Показатель политропы	Теплоемкость процесса
Изохорный	v=const	n=±∞	c=cv
Изобарный	p=const	n=0	c=cp
Изотермичский	T=const	n=1	c=±∞
Адиабатичский	q=0 или s=const	n=k	c=0

В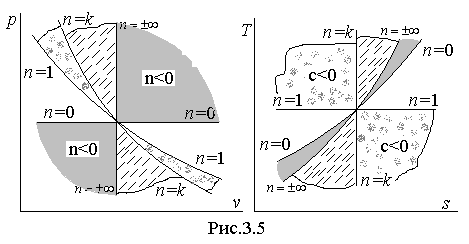 затененных секторах показатель политропы n принимает отрицательные значения.

Лекция 9