7.1.2. Массовый расход. Уравнение неразрывности

Важной характеристикой течения газа (пара) является массовый расход , т.е. масса вещества, протекающего через поверхность площадью f в единицу времени. При течении газа в каналах в одномерном приближении массовый расход определится следующим образом:

Здесь ρ=1/v - плотность газа (пара), кг/м³; v – удельный объем, м³/кг.

Логарифмическое дифференцирование позволяет записать уравнение для расхода в виде

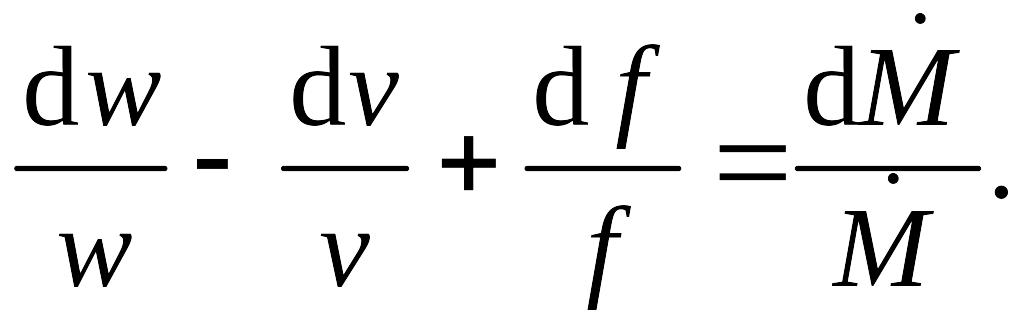
Если стенки канала непроницаемы для вещества, то, на основании закона сохранения массы, в стационарном режиме массовый расход газа (пара) через любое сечение канала будет постоянной величиной, т.е. = const. Тогда

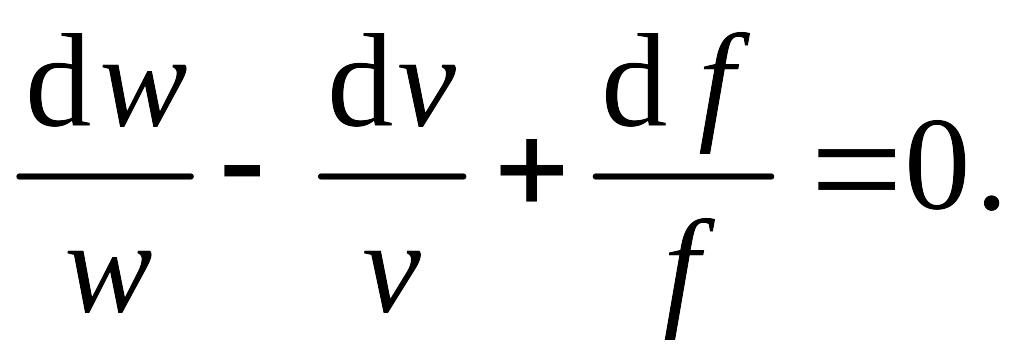
Это соотношение называют уравнением неразрывности или сплошности.

Лекция 14

7.2. Сопло и диффузор

Запишем I закон термодинамики при принятых выше допущениях с точки зрения неподвижного наблюдателя и с точки зрения наблюдателя, жестко связанного с системой:

Поскольку оба эти выражения описывают одну и ту же систему, из их сравнения находим

На основании этого выражения можно ввести два определения

сопло – канал, предназначенный для ускорения потока (dw>0) за счет уменьшения давления (dp<0);

диффузор – канал, предназначенный для увеличения давления (dp>0) за счет торможения потока (dw<0).

7.3. Скорость истечения и расход в адиабатически изолированных каналах без трения

Первый закон термодинамики легко интегрируется, так как входящие в него дифференциалы являются полными:

причем этот результат справедлив как для обратимого течения, так и для необратимого. Обычно определяют скорость w₂ потока в выходном сечении канала:

Обычно скорость на выходе сопла w₂ значительно превышает скорость на входе w₁, тогда

Разность энтальпий при течении в адиабатических соплах равна полезной внешней работе потока, откуда

В случае идеального газа на основании выражения для полезной внешней работы адиабатического процесса получаем

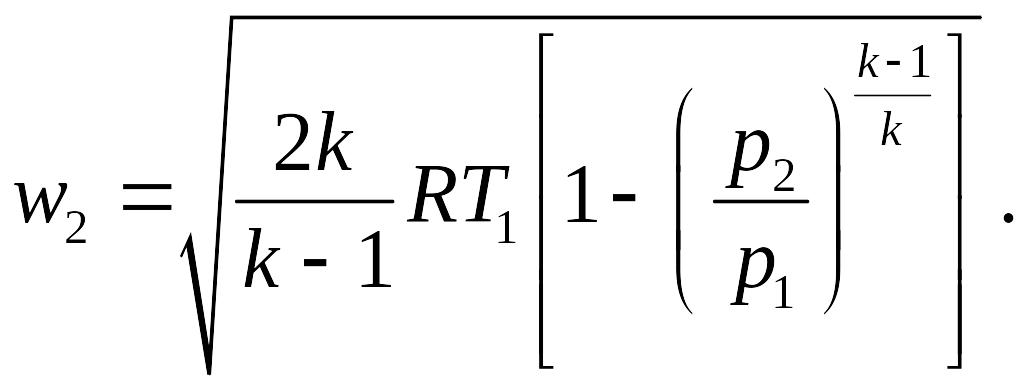
Массовый расход газа при известной скорости в выходном сечении находится на основании определения

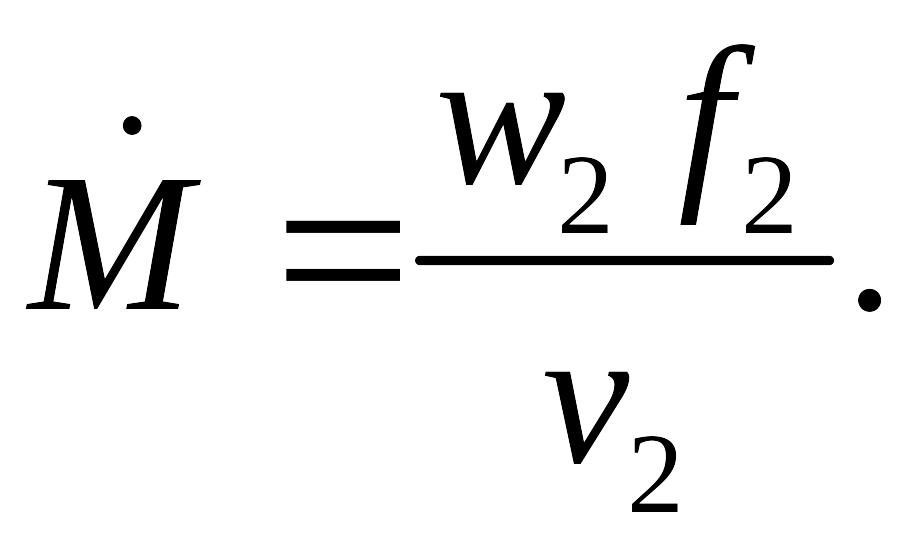
где удельный объем в выходном сечении находится из условия адиабатичности процесса, т.е.

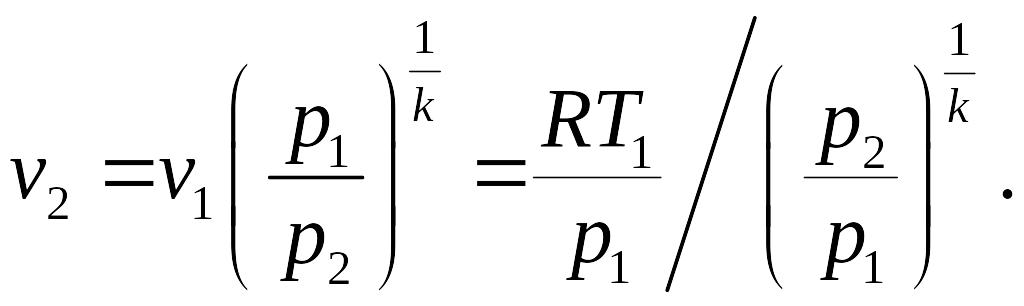
С учетом этого выражение для массового расхода идеального газа принимает вид

.

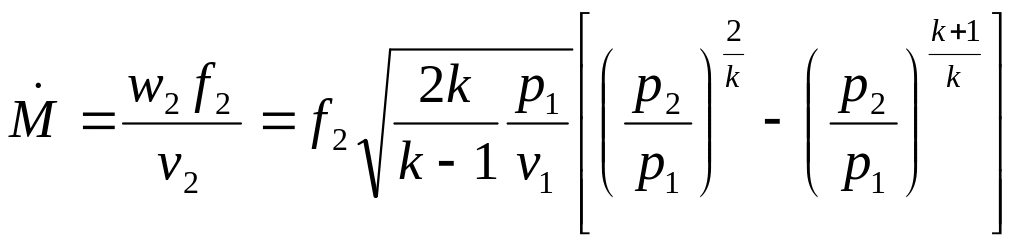Построим графики зависимости скорости истечения газа из сопла w₂ и массового расхода газа от отношения давлений за соплом p₂ и перед соплом p₁, для чего введем обозначение

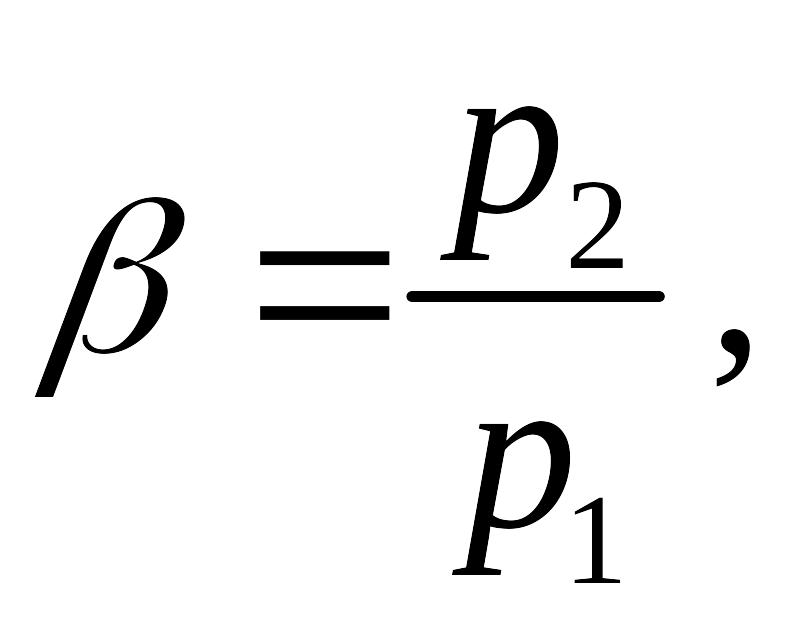
причем β может изменяться в пределах от 0 до 1, так как давление газа p₂ на выходе для сопел по определению меньше давления на входе p₁ и оба они положительны.

Для упрощения графического представления введем также безразмерные скорость истечения и массовый расход с помощью равенств

.

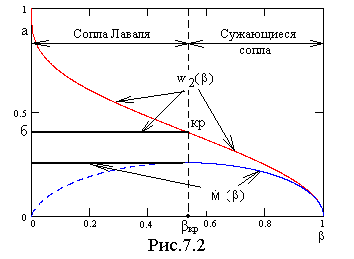
Тогда для безразмерных скорости истечения и расхода получаем следующие выражения:

.

Графики этих функций показаны на рис.7.2.

Формулы для скорости и расхода справедливы в интервале значений отношения давлений β от некоторого критического β_кр до единицы, причем при массовый расход принимает максимальное значение. В интервале же массовый расход не зависит от отношения давлений β и оказывается равным , в то время как теория дает ниспадающую до нуля ветвь. Скорость потока в этом же интервале β может вести себя двояким образом: либо возрастать с уменьшением отношения давлений, либо оставаться постоянной и равной скорости при критическом отношении давлений β_кр. Вычислим β_кр из условия максимума массового расхода:

Приравнивая числитель нулю при β= β_кр, получаем

Таким образом, критическое отношение давлений при адиабатном течении идеального газа в соплах зависит только от его показателя адиабаты, т.е. от числа атомов в молекулах газа. Значения βкр представим в таблице. Здесь же приведено ориентировочное значение критического отношения давлений для водяного пара вблизи верхней пограничной кривой, которое может быть использовано для практических расчетов.

Таблица 3

Критическое отношение давлений

Количество атомов в молекуле газа	1	2	3
Число степеней свободы f	3	5	6
Показатель адиабаты k	1.67	1.40	1.33
Критическое отношение давлений βкр	0.487	0.528	0.540

Критическому отношению давлений β_кр в соответствует скорость истечения из адиабатического сопла:

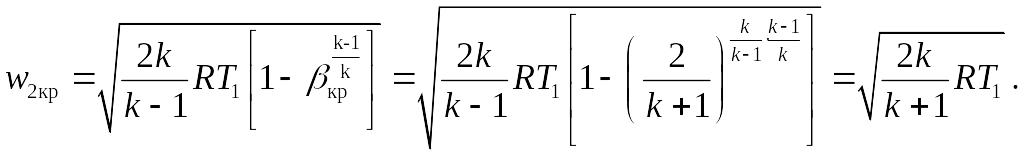
Для адиабатного процесса

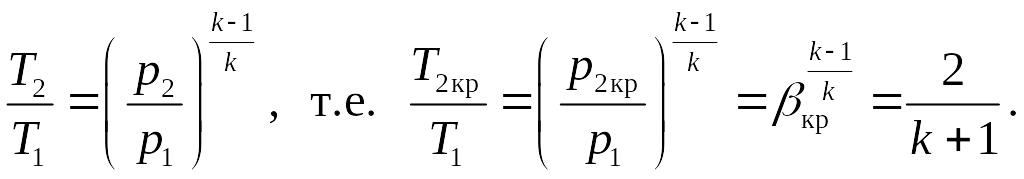
Тогда скорость истечения газа при β_кр равна

а это не что иное, как скорость звука в газах, т.е. скорость распространения малых возмущений давления, плотности и т.д. Таким образом, аномалия в поведении скорости потока в адиабатическом сопле связана с переходом от дозвукового режима течения к сверхзвуковому.

Лекция 15