5.4.4. Уравнение Клапейрона – Клаузиса

В дальнейшем будем рассматривать только фазовые переходы I рода, во время которых происходит изменение агрегатного состояния, а точнее, переход "жидкость–пар", который весьма часто имеет место в тепловых машинах.

Формула Клапейрона–Клаузиуса связывает температуру насыщения (температуру кипения) T_s с давлением насыщения p_s. Для нахождения этой зависимости запишем в дифференциальной форме условие равновесия фаз:

или

Так как химический потенциал совпадает с удельной свободной энергией Гиббса , то

откуда

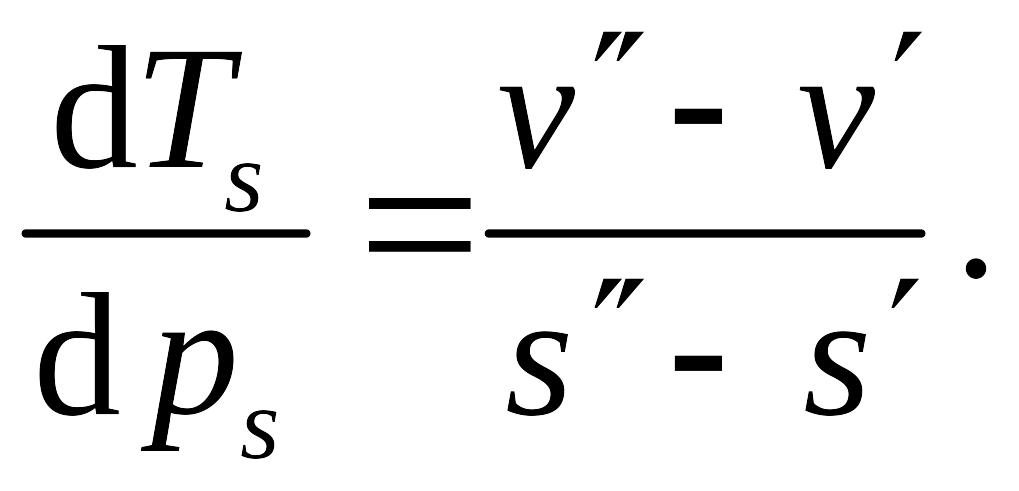
Учтя определение удельной теплоты парообразования, получаем зависимость, известную как формула Клапейрона - Клаузиуса

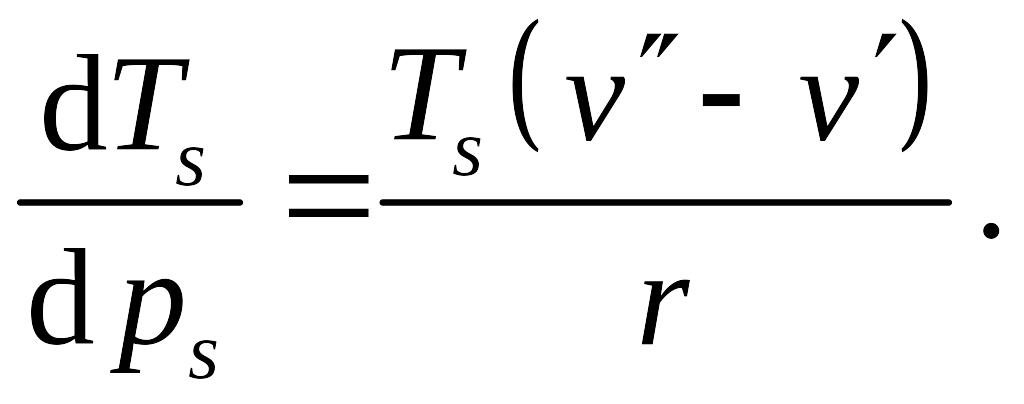
Так как , а удельный объем в парообразном состоянии больше, чем в жидком, температура кипения увеличивается с увеличением давления.

Лекция 11

6. Реальные газы (водяной пар)

6.1. Термодинамические свойства водяного пара

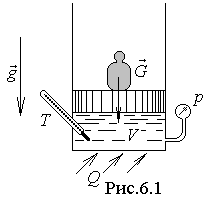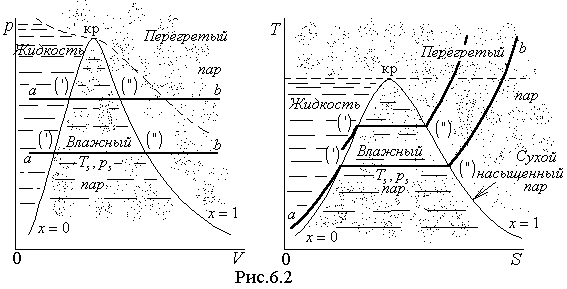
Р ассмотрим процесс фазового перехода «жидкость–пар». Пусть в цилиндре под поршнем находится 1 кг химически чистой, т.е. без примесей и растворенных в ней газов, жидкости, например воды (рис.6.1). Если пренебречь изменением гидростатического давления в жидкости, вызванного действием силы тяжести, то давление в жидкости будет постоянным по высоте и , равным внешнему давлению p. Изобразим состояние жидкости в диаграммах точкой а (рис.6.2). Будем медленно (обратимо) подводить к жидкости теплоту через стенки цилиндра. Температура жидкости будет медленно возрастать, объем ее также будет увеличиваться, но чрезвычайно мало ввиду малости коэффициента

объемного расширения жидкостей . Энтропия жидкости также будет возрастать. Давление жидкости, очевидно, останется постоянным ввиду подвижности поршня и постоянства внешней нагрузки. Процесс нагрева будет продолжаться до некоторого состояния, обозначенного на диаграммах одним штрихом ('). Начиная с этого момента, дальнейший подвод теплоты не приводит больше к изменению температуры в цилиндре. Начинается фазовый переход – превращение жидкости в пар. Но не вся жидкость мгновенно переходит в пар, количество жидкости, превратившейся в пар, оказывается пропорциональным подведенному с начала кипения количеству теплоты. Поршень теперь заметно поднимается вверх, так как удельный объем пара значительно выше удельного объема жидкости. Физически постоянство температуры во время фазового перехода при постоянном давлении объясняется тем, что в этом случае энергия, подведенная к жидкости извне в форме теплоты, тратится не на увеличение кинетической энергии молекул жидкости (пропорциональной температуре), а на изменение их потенциальной энергии взаимодействия, на разрыв связей между молекулами. Так продолжается до тех пор, пока вся жидкость не превратится в пар. Это состояние на диаграммах обозначено двумя штрихами ('').

Двухфазное состояние "жидкость-пар" носит название состояния насыщения, а температура и давление такого состояния называются параметрами насыщения . Равновесная смесь жидкости и пара в состоянии насыщения называется влажным паром. Пар в состоянии (") называется сухим насыщенным. При дальнейшем подводе тепла внешняя энергия будет вновь затрачиваться на интенсификацию хаотического движения молекул, т.е. температура пара будет возрастать. Такой пар с температурой, превышающей температуру насыщения, называется перегретым паром. При изменении внешнего давления p процесс фазового перехода происходит подобным образом с тем отличием, что с увеличением давления точки начала кипения (') смещаются в диаграммах вправо, а точки окончания кипения (") – влево. Такая ситуация имеет место до некоторого давления p_кр, называемого критическим, при котором начало кипения (') и окончание кипения (") совпадают. Такое состояние называется критическим. Температура и удельный объем в критической точке также строго определены. Для воды критические параметры имеют следующие значения: p_кр=221.15 бар, T_кр=647.27 К=374.12^оС, v_кр=0.00315 м³/кг.

Геометрическое место точек начала кипения (') в диаграммах называется нижней пограничной кривой, а геометрическое место точек окончания кипения (") – верхней пограничной кривой (рис.6.2). Вместе они составляют просто пограничную кривую. Верхняя и нижняя ветви пограничной кривой сходятся в критической точке. Область на диаграммах , ограниченная пограничной кривой, называется областью влажного пара, это область двухфазного состояния вещества. В этой области давление и температура однозначно связаны: или .

Количество теплоты, затраченное на фазовый переход при постоянных давлении и температуре может быть рассчитано на основе первого закона термодинамики для изобарного процесса и второго закона – для изотермического:

Величина r , представляющая собой количество теплоты, затраченное на превращение единицы массы кипящей жидкости в сухой насыщенный пар при постоянном давлении, носит название удельной (или скрытой) теплоты парообразования.

Параметры влажного пара

Ввиду того, что влажный пар представляет собой равновесную смесь двух фаз – кипящей жидкости и сухого насыщенного пара, его параметры будут определяться соотношением масс этих фаз (за исключением температуры и давления, которые для них одинаковы). Зависимость удельных параметров для влажного пара может быть получена с использованием свойства аддитивности экстенсивных параметров смеси. Для полных величин – массы, объема, внутренней энергии, энтальпии, свободной энергии Гельмгольца, свободной энергии Гиббса и энтропии – можно записать

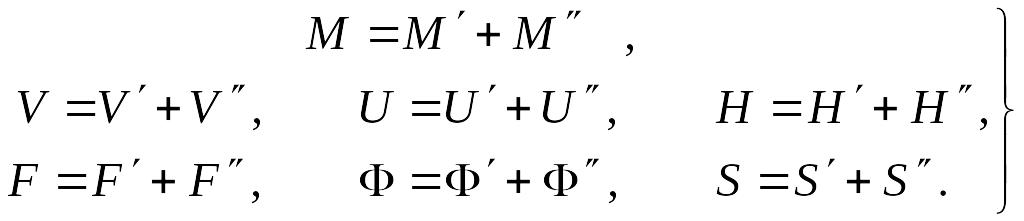
Каждая из этих величин пропорциональна массе, т.е.

,

где А – любая из перечисленных выше полных величин для влажного пара,

А' – то же для кипящей жидкости, А" –для сухого насыщенного пара. Тогда

или для удельной величины а

.

Отношение массы сухого насыщенного пара во влажном паре к массе влажного пара называется степенью сухости влажного пара:

Очевидно, что степень сухости пара x изменяется в пределах . При х = 0 жидкость находится в состоянии насыщения на нижней пограничной кривой (кипящая жидкость). При х = 1 в состоянии насыщения на верхней пограничной кривой находится сухой насыщенный пар. Линии х=const, которые имеют смысл только в области влажного пара, называются линиями постоянной степени сухости и сходятся в критической точке. Используя определение степени сухости, получаем следующие выражения для вычисления удельных параметров влажного пара:

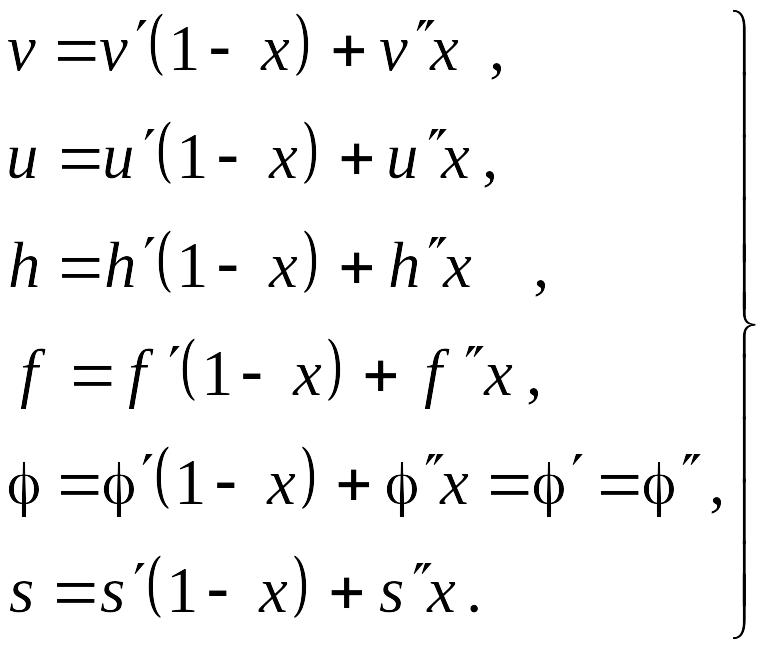
Таким образом, термодинамические функции влажного пара могут быть вычислены при заданной степени сухости х и значениях удельных параметров на нижней и верхней пограничных кривых, которые приводятся в таблицах термодинамических свойств веществ.

Лекция 12