2.Метод Гаусса — Жордана

Метод Гаусса — Жордана (метод полного исключения неизвестных) используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана.

Алгоритм

1. Выбирают первую колонку слева, в которой есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этой колонке есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранной колонки.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

Пример

Для решения следующей системы уравнений:

запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

Проведём следующие действия:

• К строке 2 добавим: −4 × Строку 1.

• К строке 3 добавим: −9 × Строку 1.

Получим:

• К строке 3 добавим: −3 × Строку 2.

• Строку 2 делим на −2

• К строке 1 добавим: −1 × Строку 3.

• К строке 2 добавим: −3/2 × Строку 3.

• К строке 1 добавим: −1 × Строку 2.

В правом столбце получаем решение:

3.Метод Крамера

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Создан Габриэлем Крамером в 1751 году.

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

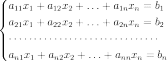
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

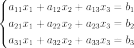
Определители:

Решение:

Пример:

Определители:

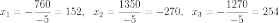
Из-за высокой вычислительной сложности метода — требуется вычисление n + 1 определителя размерности , он не применяется для машинного решения больших СЛАУ. Время, необходимое на вычисление одного определителя примерно такое же, как и время на решение одной системы уравнений при использовании метода Гаусса. Однако он иногда используется при ручном счёте и в теоретических выкладках.