МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО

«ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Методические указания к выполнению лабораторных работ № 1, 2 по дисциплине «Методы вычислений» для студентов направлений подготовки бакалавров 231000 – «Программная инженерия»

Махачкала 2014

УДК 681.3

Методические указания к выполнению лабораторных работ №1,2 по дисциплине «Методы вычислений» для студентов направления подготовки бакалавров 231000 – «Программная инженерия». Махачкала: ДГТУ, 2014. -31 с.

Указания содержат описание лабораторных работ по темам:

1. Абсолютная и относительная погрешности

2. Методы решения систем линейных алгебраических уравнений

Выполнение этих работ позволит студентам приобрести практические навыки использования Microsoft Excel для реализации численных методов, позволяет сформировать понимание математического содержания конкретного метода и умение использовать современные программные средства. В ходе выполнения лабораторных работ студенты получают возможность использовать знания, полученные при изучении дисциплин «Информатика», «Языки программирования».

Составитель: старший преподаватель кафедры

Прикладной математики и информатики, к.т.н. Мирземагомедова М.М.

Рецензенты:

Доцент кафедры ИТиПИвЭ ДГТУ, к.э.н., Мурадов М.М.

Доцент кафедры ММвЭ ДГИНХ, к. ф.-м.н. Атагишиева Г.С.

Печатается согласно постановлению

Ученого Совета Дагестанского Государственного Технического Университета.

от «______»_______________2014г.

Оглавление

ЛАБОРАТОРНАЯ РАБОТА№ 1 АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ 4

ЛАБОРАТОРНАЯ РАБОТА № 2 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 9

1.Ме́тод Га́усса 11

2.Метод Гаусса — Жордана 14

3.Метод Крамера 16

4.Матричный метод 17

5. Метод прогонки 19

ПРИЛОЖЕНИЕ 28

Лабораторная работа№ 1 абсолютная и относительная погрешности

Цель работы: изучение влияния различных видов погрешностей на результаты вычислений на ЭВМ, приобретение практических навыков использования Microsoft Excel для реализации методов нахождения погрешностей вычислений.

Пусть X точное значение, х при­ближенное значение некоторого числа.

Абсолютная погрешность приближенного числа равна модулю разности между его точным и приближенным значениями:

Однако точное значение X зачастую неизвестно, поэтому вместо абсо­лютной погрешности используют понятие границы абсолютной по­грешности:

Число Δх* заведомо равно или превышает значение абсолютной по­грешности Δх и называется предельной абсолютной погрешностью.

Часто применяется запись: X = х± Δх*.

Следует отметить, что абсолютная погрешность не полностью ха­рактеризует результат. Например, абсолютная погрешность в I мм никчемна при оценке расстояния от Москвы до Рио-де-Жанейро и абсурдна при поиске расстояний между молекулами твердого вещества. Поэтому основной характеристикой точности является относительная погрешность.

Относительная погрешность — это отношение абсолютной по­грешности к приближенному значению числа:

Относительная погрешность иногда измеряется в процентах, тогда

Действия над приближенными числами. Результат действий над приближенными числами представляет собой также приближенное число. Погрешность результата может быть выражена через погреш­ности первоначальных данных по нижеследующим правилам.

1. При сложении или вычитании чисел их абсолютные погрешно­сти складываются: Δ (a±b) = Δa + Δb.

2. 

   Относительная погрешность разности или суммы двух чисел вычисляется по формулам:

3. 

   При умножении или делении чисел друг на друга их относи­тельные погрешности складываются: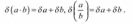

3. При возведении в степень приближенного числа его относи­тельная погрешность умножается на показатель степени: δ(а^к) = кδа.

Погрешность функции. Общая формула для оценки предельной абсолютной погрешности функции нескольких переменных u=f(x₁, x₂,...,x_n) имеет вид:

где Δх*_i — предельная абсолютная погрешность числа x_i (i= 1, 2, ...,n ).

Задание I. Пользуясь мастерам функции вспомнить основные функции Microsoft Excel и особенности их вычисления. Протабулировать функции и на отрезке [-3 ; 3] с шагом h = 1, построить графики данных функций.

Графики функций

Рис. 1.1. Значения и графики функции и на отрезке [-3 ; 3]

При выполнении задания 1 вводится только левый конец отрез­ка— значение х =-3 (ячейка В2), затем в ячейки С2, В3, В4 записываются соответствующие формулы и распространяются вправо. Значения функций у1, у2 выведены с тремя знаками после запятой (Формат/Ячейки/Число).

При построении графика выбирается тип диаграммы «точеч­ный», затем готовый график редактируется по образцу (см. рис. 1.1) с помощью команд: Формат оси (установить по оси Ох min=-3, тах=3, цену основных делений=1), Формат области построения, Парамет­ры диаграммы.

Задание 2. В ходе вычислений получены приближенные значения некоторых величин: а = 5,256 , b= 2,892 . Установить, какой из ре­зультатов более точен, если известны их истинные значения: А = 5,158 и В = 2,814 .

Для решения задачи использовать табличный процессор Microsoft Excel, рекомендуемый вид экрана приведен на рис. 1.2.

Рис.1.2. Сравнение относительных погрешностей приближенных величин

При решении задания 2 вводятся начальные значения в ячейках С4:С5: Е4;Е5. Остальные значения рассчитываются средствами Microsoft Еxcel по формулам, приведенным выше. Для отображения относительной погрешности в процентах, установите соответствующий формат ячейки.

Задание 3. Известно, что

, где А=1,34±0,02; B=7,98±0,05;С=52,74±0,1.

1. Найти предельную абсолютную погрешность Δх^* функции х . Исходная функция х является функцией трех переменных: а, b, с. Для оценки предельной абсолютной погрешности воспользуемся формулой:

Найдем частные производные функции

Риc. 1.3. Типовой экран для вычисления абсолютной и относительной погрешностей функции х(а, b. с)

Введем исходные данные в блок АЗ:В8 (см. pис. 1.3). В ячейках СЗ:С8 вычислим значения

И ячейку F10 запишем формулу

для вычисления предельной абсолютной погрешности

2. Найти абсолютную погрешность Δх функции х

В ячейках D3:D8 рассчитаем верхнюю оценку значений переменных: а_в=1,34+0,02 (=А4+В4), аналогично b_в, с_в. В ячейке В10 вычислим верхнюю оценку значения функции

Нижняя оценка значения функции вычисляется в ячейках ЕЗ:Е8 и В11 аналогично

Значение абсолютной погрешности функции ищется по формуле

в ячейке F11. Найденная абсолютная погрешность (ячейка F11) должна быть не больше предельной абсолютной погрешности (ячейка F10), т.е. должно выполняться условие: Δх ≤ Δх*.

3. Вычислить относительную погрешность δх функции х. Исходные данные позволяют вычислить значение х при а=1,34; b=7_,98; c=52,74 в ячейке В12, а к ячейке F12 — рассчитать значение относительной погрешности δх, используя найденное выше значение абсолютной погрешности Δх.

4. Оценить предельную относительную погрешность функции x.

Предельная относительная погрешность заданной функции, согласно рассмотренным выше формулам, представима в виде

Запишите полученную формулу в ячейку F13. Убедитесь в том, что значение относительной погрешности не превосходит значения предельной относительной погрешности, т,е, δх ≤ δх* .

Примеры решения задач.

Пример 1. Найти предельную абсолютную погрешность функции

при заданных значениях А==4±0,01; В=7±0,04.

Решение

Пример 2. Найти предельную абсолютную погрешность функции y=a-b при заданных значениях А==4±0,01; В=7±0,04.

Решение

Пример 3. Найти абсолютную погрешность функции

при заданных значениях a=4±0,01; b=7±0,04; C=5±01.

Решение.

Пример 4.Найти предельную относительную погрешность функции

при заданных значения a=4±0,01; b=7±0,04;

Решение.

Пример 5. Найти предельную относительную погрешность функ­ции

при заданных значениях a=4±0,01; b=7±0,04;

Решение

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Задание 4. Скопировать задание 3 на новый лист. Внести данные своего варианта в ячейки AЗ:В8 (см. рис. 1.3) из таблицы I приложе­ния. Вычислить х_в, х_н, х (ячейки B10, В11, В12). Вычислить частные производные и заполнить формулами ячейки С4. С6, С8. Изменить формулу вычисления предельной относительной погрешности δх* в ячейке F13, пользуясь основными правилами. Все остальные ячейки пересчитаются автоматически. Оформить отчет для своего варианта.

Задание 5. Решить в тетради следующую задачу.

Известно, что A=4±0,01; B=8±0,04; С=5+0,1. Найти предельную относительную погрешность δу*следующих функций:

Найти предельную абсолютную погрешность Δу*следующих функций: