4. Автоколебания

Рис. 21.25

Системы, совершающие незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами, называются автоколебательными. Любая автоколебательная система состоит из следующих основных частей (рис. 21.25): 1) источника энергии, компенсирующего потери энергии на преодоление сил сопротивления; 2) колебательной системы; 3) "клапана" — устройства, дозировано регулирующего подвод энергии в колебательную систему; 4) обратной связи — устройства, управляющего работой клапана с помощью процессов, протекающих в колебательной системе.

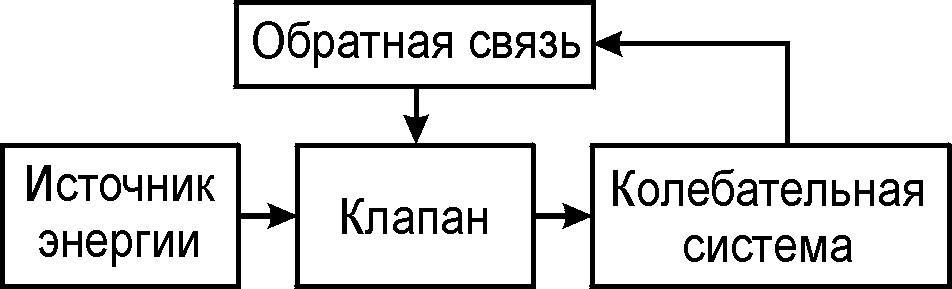
Рассмотрим в качестве примера модель электромеханической автоколебательной системы (рис. 21.26). В этом случае источником энергии служит батарея E, колебательной системой — пружинный маятник M, клапаном — контакт-прерыватель K, а обратная связь осуществляется с помощью электромагнита ЭМ, притягивающего стальной шарик маятника. В начальный момент контакт замкнут, по цепи протекает ток, и шарик маятника притягивается к электромагниту; при этом контакт разрывается и маятник приходит в колебательное движение. При возвращении шарика в исходное состояние контакт снова замыкается, и колебания возобновляются.

Рис. 21.26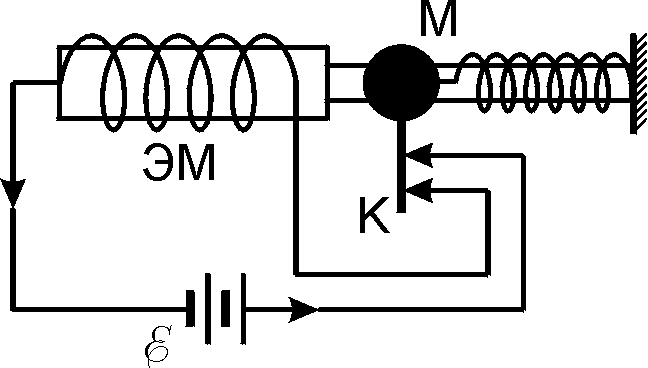

Аналогичные автоколебательные механизмы используют также в механических часах, отбойных молотках, двигателе внутреннего сгорания и других устройствах.

Принято различать положительную и отрицательную обратную связь.

В случае положительной обратной связи направления внешней силы и скорости колебательной системы совпадают. В этом случае источник энергии производит над колебательной системой положительную работу, т.е. передает ей энергию.

В случае отрицательной обратной связи направления внешней силы и скорости взаимно противоположны и колебания системы затухают быстрее, чем в отсутствие обратной связи.

В рассматриваемом примере знак обратной связи можно изменить, перемещая электромагнит.

5. Спектр колебаний

Любое сложное колебательное движение может быть представлено как совокупность гармонических колебаний с различными частотами и амплитудами. Совокупность таких колебаний называется спектром. Для того, чтобы найти спектр колебаний, т.е. разложить сложное колебательное движение на отдельные гармонические составляющие, поступают следующим образом.

Пусть сложное колебание описывается периодической (с периодом T), но не гармонической функцией f(t)=f(t+T). По теореме Фурье эту функцию можно представит в виде суммы гармонических составляющих:

,

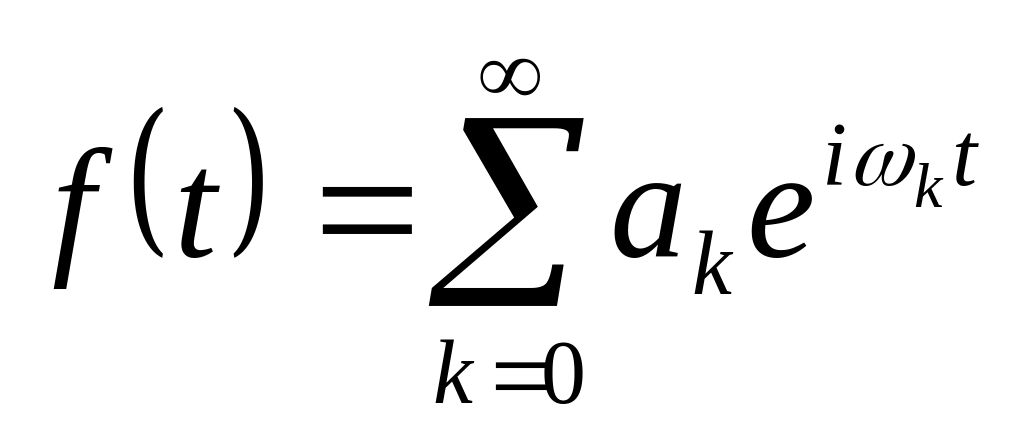(21.71)

где ; гармоническое колебание с амплитудой ak и частотой k называют часто гармоникой. Основная гармоника (k=1) с частотой ₁ = ₀ называется тоном, гармоника с частотой Δk = 2 Δ₀,... — обертоном.

Для нахождения амплитуд гармоник умножим (21.71) на и проинтегрируем в пределах от 0 до T:

,

(21.72)

Интеграл в правой части (21.72) легко вычисляется:

.

Таким образом, в сумме, которая фигурирует в правой части (21.72), остается только одно слагаемое с k=n. Поэтому

.

Рис. 21.27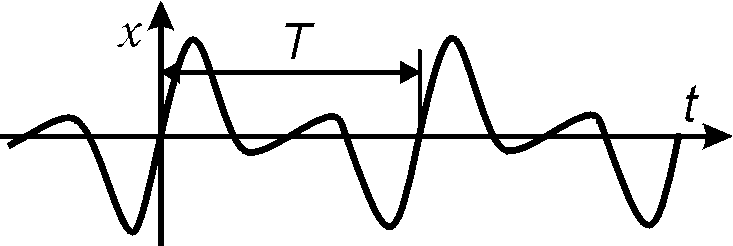

На рис. 21.27 как пример показан график сложного колебания, являющегося суммой трех гармоник:

.

Из этого графика практически невозможно определить число гармоник, их амплитуды и частоты. Если же построить спектр этого колебания, т.е. зависимость амплитуды от частоты (рис. 21.28), то непосредственно видно, что рассматриваемое колебание состоит их трех гармоник с амплитудами A_=2, A₂=3, A₃= и частотами _, ₂2, ₃3 c^-1.

Чем сильнее исходное колебание отличается от гармонического, тем богаче его спектр, т.е. тем больше гармоник содержится в разложении (21.71). В общем случае спектр сложного колебания содержит бесконечный ряд гармоник, амплитуды которых быстро убывают с увеличением их номера, так что практически в разложении (21.71) приходится принимать во внимание только некоторое конечное число обертонов. Экспериментально гармоники могут быть найдены с помощью набора осцилляторов, собственные частоты которых выбраны с определенным шагом (частотомер). Тогда при воздействии сложного импульса на этот набор будут резонировать те из осцилляторов, собственные частоты которых близки к частотам гармоник в разложении (21.71).