1. Вынужденные колебания

Чтобы колебания были незатухающими, нужно восполнять потери энергии, затраченной на работу против сил сопротивления. Это можно сделать, воздействуя на систему периодически действующей силой , где  — частота, а F₀ — амплитудное значение внешней силы.

Уравнение вынужденных колебаний получим из уравнений затухающих колебаний (21.32), записав в правой части вместо нуля выражение для вынуждающей силы, деленное на массу:

,

(21.47)

Если колебательная система первоначально покоилась, то при воздействии периодической силы она придет в колебательное движение с частотой, равной частоте вынуждающей силы, и с постоянно возрастающей амплитудой. Далее, когда потери энергии на работу против сил сопротивления будут компенсироваться работой вынуждающей силы, система будет колебаться с некоторой постоянной амплитудой.

Решение дифференциального уравнения (21.47) для этого случая будет иметь вид

,

(21.48)

Для нахождения амплитуды A и начальной фазы  вынужденных колебаний найдем первую и вторую производные по x:

и совместно с (21.48) подставим в (21.47). В результате получим

.

(21.49)

Для определения амплитуды A умножим (21.49) на комплексно-со­пря­жен­ное выражение, т.е. на

.

Тогда ,

откуда

.

(21.50)

Для вычисления начальной фазы вынужденных колебаний приравняем к нулю и мнимую часть (21.49):

,

откуда

.

(21.51)

Проанализируем теперь зависимости амплитуды и начальной фазы колебаний от частоты вынуждающей силы . При =0 . Эта величина называется статической амплитудой. Далее по мере нарастания частоты  амплитуда сначала возрастает, а затем при    A  0, т.е. при некоторой частоте вынуждающей силы зависимость A() будет иметь максимум. Явление резкого возрастания амплитуды вынужденных колебаний при называется резонансом. Частота , при которой , называется резонансной.

Для нахождения резонансной частоты заметим, что амплитуда вынужденных колебаний достигает максимального значения, когда подкоренное выражение в (21.50) минимально. В минимуме первая производная равна нулю:

,или ,

откуда после несложных преобразований находим

,

(21.52)

Максимальное значение амплитуды вынужденных колебаний найдем, подставив из (21.52) в (21.50):

.

(21.53)

Из (21.52) видно, что резонанс всегда наблюдается при частоте, меньшей, чем частота собственных колебаний системы, причем по мере роста коэффициента затухания  уменьшается как значение резонансной частоты, так и резонансной амплитуды (рис. 21.15).

Рис. 21.15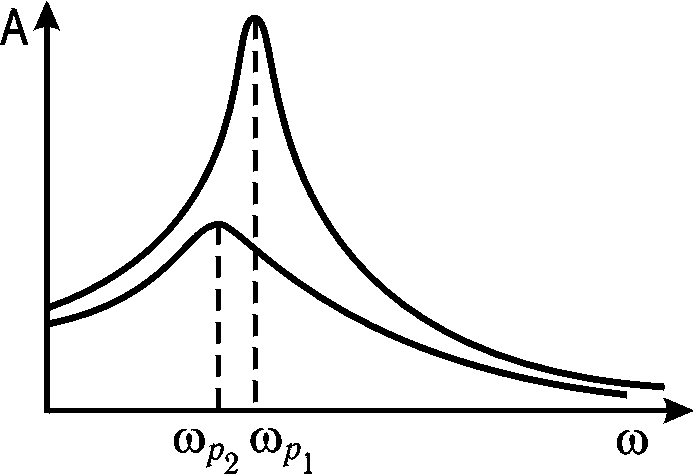

Как видно из формулы (21.51), при , а при      . Графическая зависимость  показана на рис. 21.16.

Рассмотрим теперь зависимость скорости системы, совершающей вынужденные колебания, от частоты вынуждающей силы.

Скорость системы в любой момент определяется выражением

,

Рис. 21.16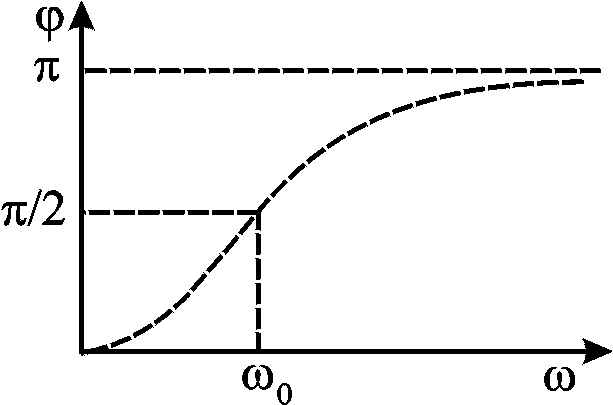

из которого видно, что амплитудное значение скорости

,

Согласно (21.50) это выражение можно записать в виде

или

.

(21.54)

Рис. 21.17

Нетрудно видеть, что при   0 или    скорость v  0 и, следовательно, зависимость v имеет вид, изображенный на рис. 21.17.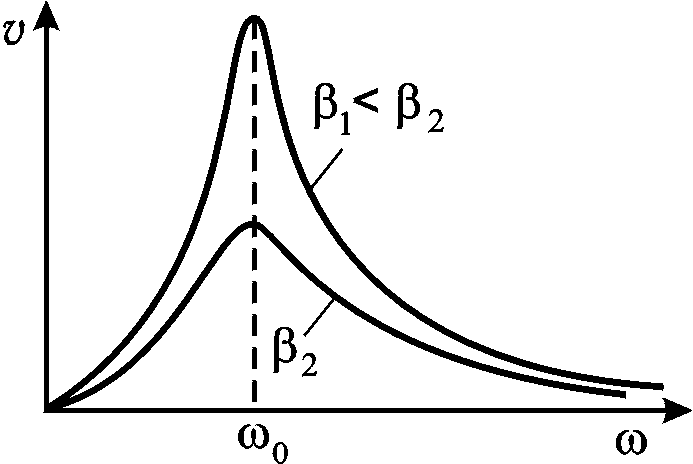

Приравнивая к нулю производную подкоренного выражения в (21.54), получаем _р  ₀, т.е. максимальное значение скорости (резонанс скоростей) наблюдается на частоте собственных колебаний системы и не зависит от значения коэффициента затухания.

Важной характеристикой резонансной кривой является ее ширина, т.е. интервал частот  вблизи от резонанса, в пределах которого A  0,7A_p. Можно показать, что ширина резонансной кривой однозначно связана с коэффициентом затухания —   , что позволяет определять этот важный параметр колебательной системы по графику зависимости A.

Исследование колебательных систем методом возбуждения в них вынужденных колебаний и последующего изучения резонансной кривой позволяет (также как и при изучении затухающих колебаний) определить коэффициент затухания и собственную частоту колебаний системы.