Затухающие колебания

В реальных условиях и системах, совершающих колебания, всегда присутствуют силы сопротивления. В результате система постепенно расходует свою энергию на выполнение работы против сил сопротивления, и колебания в конце концов прекращаются.

Рис. 21.11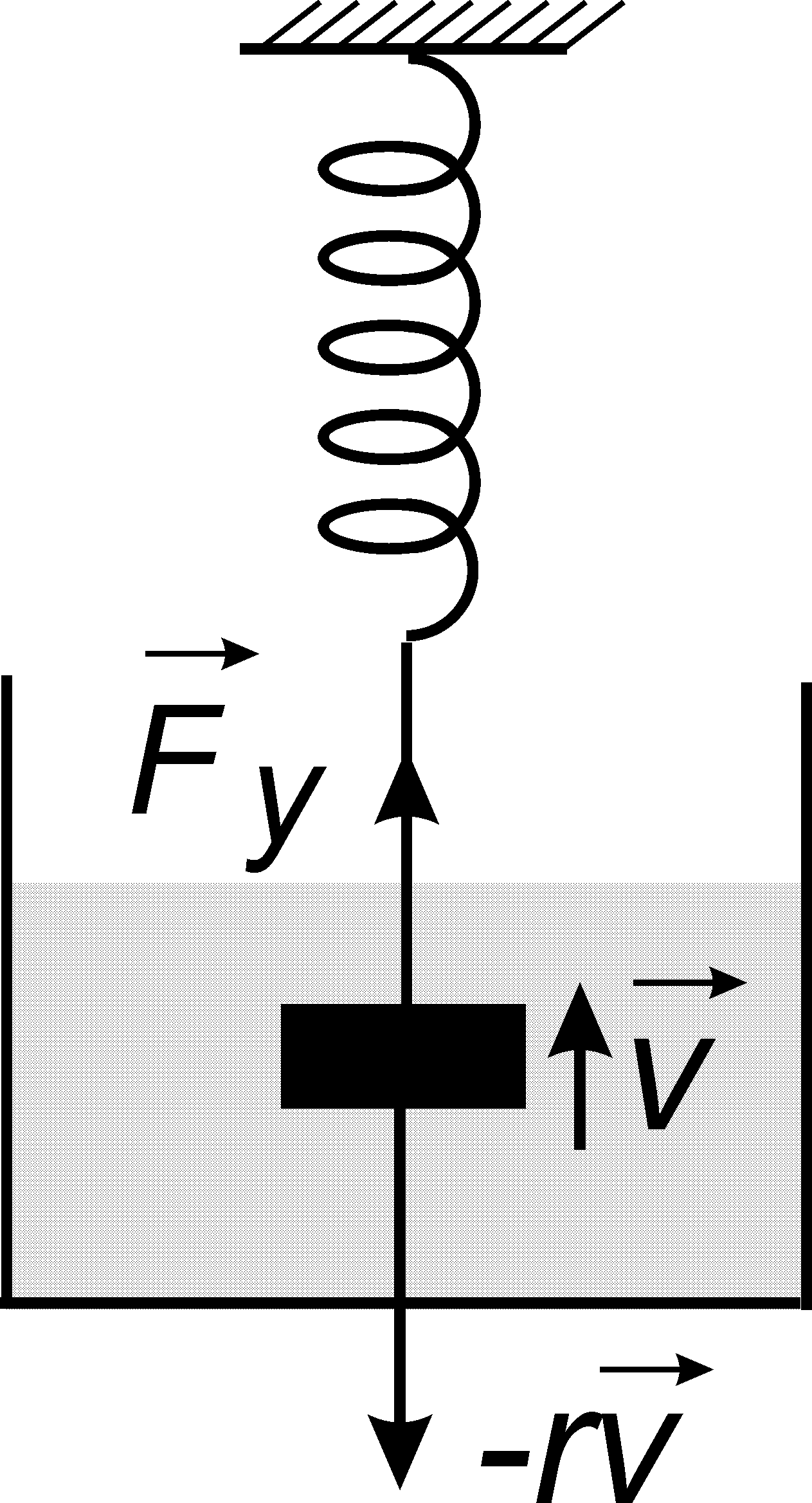

В том случае, когда силой сопротивления является сила вязкости (внутреннего трения), ее значение определятся выражением

,

(21.31)

где r — коэффициент сопротивления, значение которого зависит от вязкости среды, в которой движется колебательная система, а также от формы и размеров движущейся системы (рис. 21.11).

Суммарная сила, действующая на колебательную систему, будет

,

где F_y = –kx — упругая сила.

Используя второй закон Ньютона, можно записать

или

.

Последнее уравнение представляет собой дифференциальное уравнение затухающих колебаний, которое обычно представляют в виде

,

(21.32)

где — коэффициент затухания; а — циклическая частота собственных свободных колебаний той же системы при=0.

Решение уравнения (21.32) будем искать в виде (21.3) в предположении, что амплитуда A является убывающей функцией от времени:

.

(21.33)

Найдем первую и вторую производные по времени

,	(21.34)
,	(21.35)

Далее подставим (21.33) – (21.35) в дифференциальное уравнение (21.32). После сокращения на получим

.

В последнем выражении приравняем к нулю действительные и мнимые части:

Re:	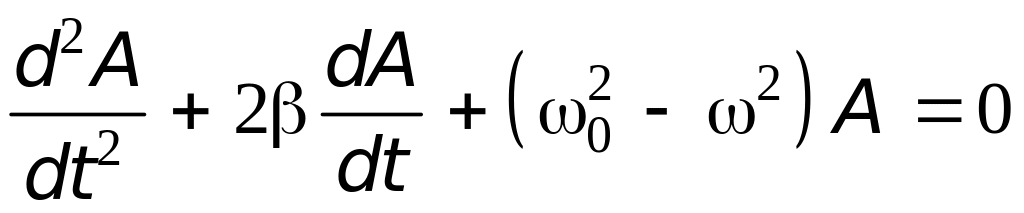,	(21.36)
Im:	,	(21.37)

Решаем вначале уравнение (21.37)

, ,
, ,
, ,	(21.38)

т.е. амплитуда затухающих колебаний убывает со временем по экспоненциальному закону.

Подставив (21.38) в (21.36), получим

,

откуда

,

(21.39)

т.е. циклическая частота затухающих колебаний  всегда меньше частоты незатухающих собственных колебаний ₀ той же системы.

С учетом (21.38) общее решение (21.33) представим в виде

.

(21.40)

Рис. 21.12

График затухающих колебаний показан на рис. 21.12.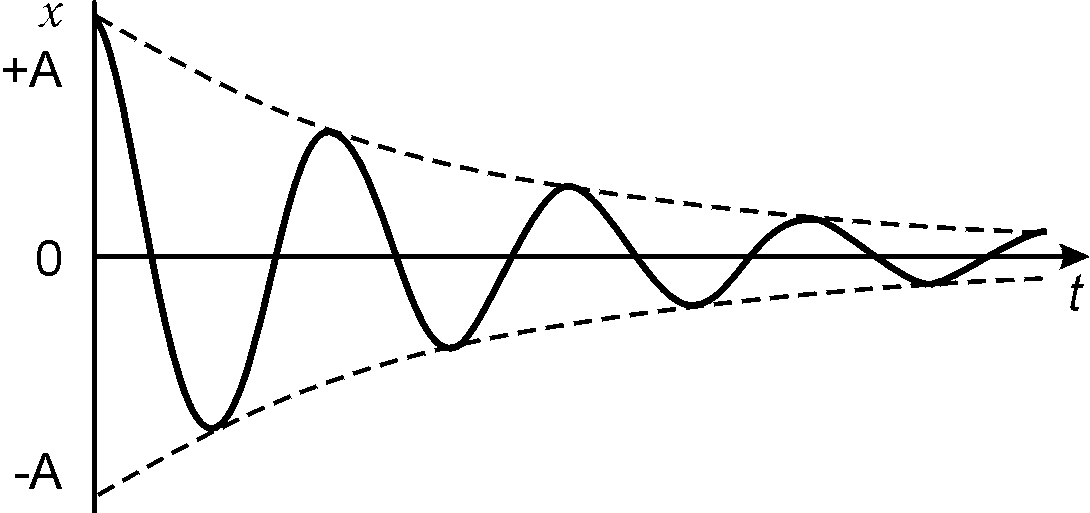

Одна из характеристик реальной колебательной системы — величина, называемая логарифмическим декрементом затухания, которая определяется соотношением

,

(21.41)

где A(t) и A(t+T) — амплитуды колебаний, взятых через промежуток времени, равный периоду колебаний T.

Подставив в (21.41) значения A(t) и A(t+T) из (21.36), получим

.

(21.42)

В ряде случаев для характеристики реальных колебательных систем удобно использовать параметр Q — добротность системы. По определению добротность системы

,

(21.43)

где W(t) — полная энергия колебательной системы; ΔW(t) — энергия, затраченная на преодоление сил сопротивления за период одного колебания.

Можно показать, что добротность и логарифмический декремент затухания связаны соотношением

.

(21.44)

Приведенное рассмотрение относилось к случаю не очень сильного затухания, точнее, коэффициент затухания  удовлетворял условию _. Рассмотрим теперь случай, когда затухание велико, т.е. >_. Тогда подкоренное выражение в (21.39) становится отрицательным, а частота  мнимой:

.

В этих условиях решение (21.40) (при 0=0) описывает апериодическое движение:

,

г рафик которого изображен на рис. 21.13. Видно, что в любой момент времени x(t)>0. Это означает, что система, будучи выведенной из состояния равновесия, медленно возвращается к нему и не "проскакивает" его.

Режим колебаний при =_ называется критическим. Критический режим является граничным между затухающими колебаниями (_) и апериодическим движением (>_). Критический режим по сравнению с другими выгодно отличается тем, что в таком режиме система быстрее всего возвращается в положение равновесия. Это обстоятельство используется в различных измерительных приборах, в которых указатель (обычно стрелка) прибора продвигается к необходимому делению за оптимальное время (рычажные весы, стрелки электроизмерительных приборов и т.д.).

Затухающие колебания используют для определения параметров колебательной системы. Измерив на опыте частоту  (или период T) затухающих колебаний и логарифмический декремент затухания , можно из (21.42) найти коэффициент затухания , а из (21.39) — частоту собственных колебаний системы ₀.

В заключение отметим, что в механических колебательных системах зачатую силой сопротивления является сила внешнего (сухого) трения, значение которой не зависит от скорости движения. В этом случае приведенный выше анализ неприменим. Не вдаваясь в детальный математический анализ, отметим лишь характерные особенности движения таких колебательных систем.

1. Амплитуда колебаний в этом случае убывает по линейному закону

.

2. Частота затухающих колебаний равна частоте собственных колебаний:  =₀.

Лекція 9.