8.2 Сложение гармонических колебаний с близкими частотами. Биения

Пусть складываются два гармонических колебания с одинаковыми амплитудами, одинаковыми начальными фазами, но с различными, хотя и близкими частотами:

,
.

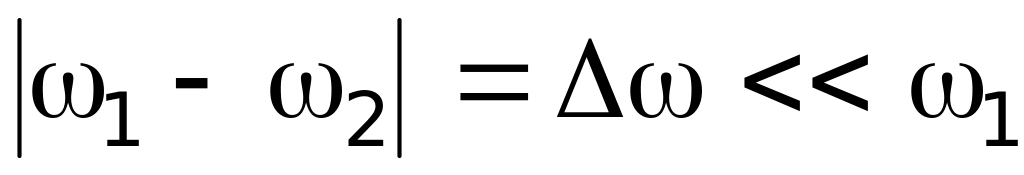Результирующее колебание

,
,	(21.25)

В выражении (21.25) первый множитель

(21.26)

можно рассматривать как амплитуду, медленно меняющуюся со временем с частотой . Второй сомножитель — гармоническое колебание, частота которого значительно больше частоты изменения амплитуды.

В моменты времени, удовлетворяющие условию

,

(21.27)

результирующая амплитуда становится максимальной:

,
.

Промежуток времени между двумя последовательными всплесками амплитуды называется периодом биений. с помощью (21.27) находим период биений T:

.

Между последовательными всплесками амплитуда результирующего колебания обращается в нуль. Вид биений показан на рис. 21.9.

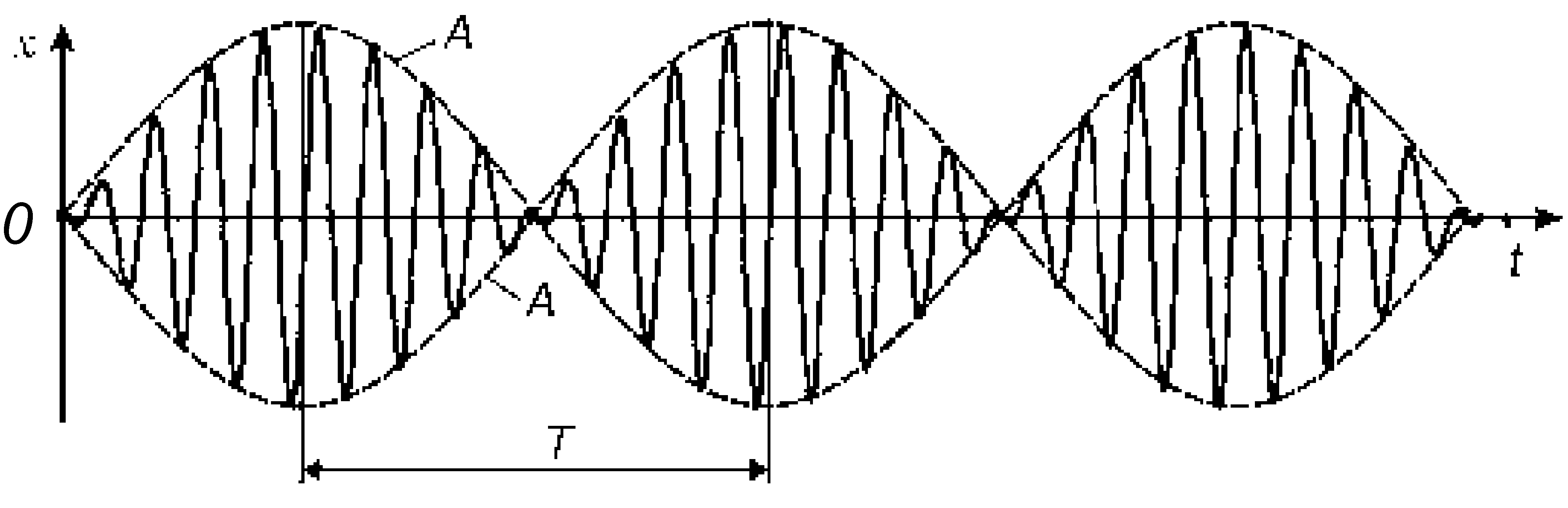
Рис. 21.9

Явление биений находит применение для измерения частоты колебаний сложением их с эталонными колебаниями известной частоты. Критерий равенства частот измеряемого и эталонного колебаний — уменьшение частоты биений до нуля. В ряде случаев явление биений используется также для понижения частоты колебаний (например, для получения колебаний звуковой частоты в электромузыкальных инструментах).

21.9. Сложение взаимно перпендикулярных (векторных) колебаний

Пусть материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях одинаковой частоты, описываемых уравнениями

,	(21.28)
,	(21.29)

Для нахождения траектории результирующего движения исключим из уравнений (21.28) и (21.29) время t. Для этого преобразуем эти уравнения к виду:

Получили линейную систему уравнений относительно sin t и cos t, решая которую, находим

Подставим полученные значения sin t и cos t в тождество sin 2t+cos 2t = 1. После несложных преобразований получим

.

(21.30)

Последнее уравнение представляет собой обобщенное уравнение эллипса.

Рассмотрим теперь несколько частных случаев.

1. Разность фаз складываемых колебаний равна нулю, т.е. ₂ –₂ = 0. Тогда из (21.30) следует

.

Из полученного выражения видно, что в этом случае траектория движения материальной точки представляет собой прямую

,

проходящую через первый и третий квадранты (рис. 21.10, а).

2. Разность фаз _  _  . Из (21.30) следует

,

т.е. в этом случае траектория тоже прямолинейна

,

но проходит через второй и четвертый квадранты (рис. 21.10, б).

3. Разность фаз . Тогда движение будет происходить по эллиптической траектории (рис. 21.10, в)

,

отнесенной к осям координат. По такой же траектории будет двигаться точка, если , однако в этом случае вращение будет проходить против часовой стрелки.

В частном случае, если A₁ = A₂, движение будет проходить по окружности.

Рис. 21.10

При любых других значениях разности фаз траекторией движения будет эллипс, не приведенный к осям координат (рис. 21.10, г).

Более сложные криволинейные траектории получаются при сложении взаимно перпендикулярных колебаний различной частоты. В тех случаях, когда отношение частот выражается рациональным числом, траектории представляют собой замкнутую кривую, называемую фигурой Лиссажу, в других же случаях кривая будет незамкнутой.

Фигуры Лиссажу находят применение для определения частоты и формы складываемых колебаний. Исследование формы колебаний основано на том, что наш глаз четко улавливает малейшие отклонения от прямой или эллипса, которые вызываются тем, что складываемые колебаний не имеют строго синусоидальной формы.

Лекція 8.